녹원학원 수학과학영재교육 010-3549-5206
SAT AMC8/10/12 영재원대비 KMO 수학과학경시올림피아드 053-765-8233
2025년 6월 20일 금요일
국제 올림피아드 영재 교육… 삼성·한화서 지원한다…기업 첫 후원
2025년 4월 19일 토요일
경북대학교 과학영재교육원 신입생 선발(현재 초6· 중1학년대상) 모집요강
2025년 3월 22일 토요일
2025년 3월 8일 토요일
2025 AMC 8 Problems
Problem 1
The eight-pointed star, shown in the figure below, is a popular quilting pattern. What percent of the entire
![[asy] path x = (0,1)--(1,2)--(2,2)--(1,1)--cycle; path y = reflect((0,0),(4,4)) * x; fill(x, gray(0.6)); fill(rotate(90, (2,2)) * x, gray(0.6)); fill(rotate(180, (2,2)) * x, gray(0.6)); fill(rotate(270, (2,2)) * x, gray(0.6)); fill(y, gray(0.8)); fill(rotate(90, (2,2)) * y, gray(0.8)); fill(rotate(180, (2,2)) * y, gray(0.8)); fill(rotate(270, (2,2)) * y, gray(0.8)); draw((1,1)--(3,3)); draw((3,1)--(1,3)); add(grid(4,4)); path w = (1,0)--(2,1)--(3,0); draw(w); draw(rotate(90, (2,2)) * w); draw(rotate(180, (2,2)) * w); draw(rotate(270, (2,2)) * w); [/asy]](https://latex.artofproblemsolving.com/6/f/1/6f1cc7540fcf94f876c74993194b3df4fc4a420c.png)
![]()
Problem 2
The table below shows the Ancient Egyptian hieroglyphs that were used to represent different numbers.
For example, the number ![]() was represented by the hieroglyphs
was represented by the hieroglyphs ![]() . What number is represented by the following combination of hieroglyphs?
. What number is represented by the following combination of hieroglyphs?
![]()
Problem 3
Buffalo Shuffle-o is a card game in which all the cards are distributed evenly among all players at the start of the game. When Annika and ![]() of her friends play Buffalo Shuffle-o, each player is dealt
of her friends play Buffalo Shuffle-o, each player is dealt ![]() cards. Suppose
cards. Suppose ![]() more friends join the next game. How many cards will be dealt to each player?
more friends join the next game. How many cards will be dealt to each player?
![]()
Problem 4
Lucius is counting backward by ![]() s. His first three numbers are
s. His first three numbers are ![]() ,
, ![]() , and
, and ![]() . What is his
. What is his ![]() th number?
th number?
![]()
Problem 5
Betty drives a truck to deliver packages in a neighborhood whose street map is shown below. Betty starts at the factory (labled ![]() ) and drives to location
) and drives to location ![]() , then
, then ![]() , then
, then ![]() , before returning to
, before returning to ![]() . What is the shortest distance, in blocks, she can drive to complete the route?
. What is the shortest distance, in blocks, she can drive to complete the route?
![[asy] unitsize(20); add(grid(8,6)); path w = circle((0,0),0.4); fill(w, white); draw(w); label("$B$",(0,0)); fill(shift((2,4)) * w, white); draw(shift((2,4)) * w); label("$C$",(2,4)); fill(shift((7,3)) * w, white); draw(shift((7,3)) * w); label("$A$",(7,3)); fill(shift((6,5)) * w, white); draw(shift((6,5)) * w); label("$F$",(6,5)); draw((6,-0.2)--(7,-0.2), EndArrow(3)); draw((7,-0.2)--(6,-0.2), EndArrow(3)); draw(shift(6.5, -0.48) * scale(0.03) * texpath("1 block")); draw((8.2,1)--(8.2,2), EndArrow(3)); draw((8.2,2)--(8.2,1), EndArrow(3)); draw(shift(8.88, 1.5) * scale(0.03) * texpath("1 block")); [/asy]](https://latex.artofproblemsolving.com/0/2/f/02f4d70dd8e934b785c58b9e171db52b9bca463e.png)
![]()
Problem 6
Sekou writes the numbers ![]() After he erases one of his numbers, the sum of the remaining four numbers is a multiple of
After he erases one of his numbers, the sum of the remaining four numbers is a multiple of ![]() Which number did he erase?
Which number did he erase?
![]()
Problem 7
On the most recent exam on Prof. Xochi's class,
students earned a score of at least
,
students earned a score of at least
,
students earned a score of at least
,
students earned a score of at least
.
How many students earned a score of at least 80% and less than 90%?
![]()
Problem 8
Isaiah cuts open a cardboard cube along some of its edges to form the flat shape shown on the right, which has an area of 18 square centimeters. What is the volume of the cube in cubic centimeters?
![]()
Problem 9
Ningli looks at the 6 pairs of numbers directly across from each other on a clock. She takes the average of each pair of numbers. What is the average of the resulting 6 numbers?
![[asy] /* AMC8 P9 2025, by NUMANA: BUI VAN HIEU buivanhieu@husc.edu.vn, https://husc.edu.vn */ unitsize(1cm); draw(circle((0,0),2)); for(int i = 1; i <= 12; ++i) { draw(1.9*dir(90-i*30)-- 2*dir(90-i*30));//,linewidth(1pt) label("$"+string(i)+"$",2.3*dir(90-i*30)); } draw(2*dir(-150)--2*dir(30),dashed); [/asy]](https://latex.artofproblemsolving.com/a/d/e/ade0d0a5fb7d05e6a8166bee8fda14dbe1c68178.png)
![]()
Problem 10
In the figure below, ![]() is a rectangle with sides of length
is a rectangle with sides of length ![]() inches and
inches and ![]() = 3 inches. Rectangle
= 3 inches. Rectangle ![]() is rotated
is rotated ![]() clockwise around the midpoint of side
clockwise around the midpoint of side ![]() to give a second rectangle. What is the total area, in square inches, covered by the two overlapping rectangles?
to give a second rectangle. What is the total area, in square inches, covered by the two overlapping rectangles?
![]()
Problem 11
A ![]() consists of four squares connected along their edges. There are five possible tetromino shapes,
consists of four squares connected along their edges. There are five possible tetromino shapes, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() , shown below, which can be rotated or flipped over. Three tetrominoes are used to completely cover a
, shown below, which can be rotated or flipped over. Three tetrominoes are used to completely cover a ![]() rectangle. At least one of the tiles is an
rectangle. At least one of the tiles is an ![]() tile. What are the other two tiles?
tile. What are the other two tiles?
![[asy] unitsize(12); add(grid(1,4)); label("I", (0.5,-1)); add(shift((5,0)) * grid(2,2)); label("O", (6,-1)); add(shift((11,0)) * grid(1,3)); add(shift((11,0)) * grid(2,1)); label("L", (12,-1)); add(shift((18,0)) * grid(1,1)); add(shift((17,1)) * grid(3,1)); label("T", (18.5,-1)); add(shift((25,1)) * grid(2,1)); add(shift((24,0)) * grid(2,1)); label("S", (25.5,-1)); add(shift((12,-6)) * grid(4,3)); [/asy]](https://latex.artofproblemsolving.com/f/2/1/f2172172ab6cb261dfc95f73ad4d68405a6f0ff5.png)
![]() and
and ![]() and
and ![]() and
and ![]() and
and ![]() and
and ![]()
Problem 12
The region shown below consists of 24 squares, each with side length 1 centimeter. What is the area, in square centimeters, of the largest circle that can fit inside the region, possibly touching the boundaries?
![[asy] import graph; size(100); pen gridPen = black; void drawSquare(pair p) { draw(box(p, p + (1,1)), gridPen); } int[][] grid = { {0, 0, 0, 0, 0, 0}, {0, 0, 1, 1, 0, 0}, {0, 1, 1, 1, 1, 0}, {1, 1, 1, 1, 1, 1}, {1, 1, 1, 1, 1, 1}, {0, 1, 1, 1, 1, 0}, {0, 0, 1, 1, 0, 0}, {0, 0, 0, 0, 0, 0} }; int rows = grid.length; int cols = grid[0].length; for (int i = 0; i < rows; ++i) { for (int j = 0; j < cols; ++j) { if (grid[i][j] == 1) { drawSquare((j, rows - i - 1)); } } } [/asy]](https://latex.artofproblemsolving.com/2/2/b/22b12d5f528f4fc1b25a685e25d32476c453ec95.png)
![]()
Problem 13
Each of the even numbers ![]() is divided by
is divided by ![]() . The remainders are recorded. Which histogram displays the number of times each remainder occurs?
. The remainders are recorded. Which histogram displays the number of times each remainder occurs?![[asy] /*By Reda_mandymath*/ unitsize(15); void histogram(pair p, string _str, int[] n) { /* p is shift transformation, _str is choice string, n[] is the array of number of remainders, _pen is the pen style of block, a is the width of block, b is the width of gap _scale is the font scale of labels*/ pen _pen; real a = 0.8; real b = 0.3; real _scale = 0.8; draw(shift(p) * ((0, 0) -- (9, 0) -- (9, 5) -- (0, 5) -- cycle)); label(scale(_scale) * rotate(90) * "Count", (-0.4, 2.5)+p); label(scale(_scale) * "Remainder", (4.5, -1)+p); for (int i = 0; i <= 6; ++i) { if (n[i] == 3) { _pen = mediumgray; } else { _pen = heavygray; } fill(shift(p) * ((a*(i+1) + b*i, 0) -- (a*(i+1) + b*i, n[i]) -- (a*(i+2) + b*i, n[i]) -- (a*(i+2) + b*i, 0) -- cycle), _pen); label(scale(_scale) * string(i), shift(p) * (a*(i+1.5) + b*i, 0), S); label(scale(_scale) * string(n[i]), shift(p) * (a*(i+1.5) + b*i, n[i]), N); } label(_str, shift(p) * (-0.4, 6)); } histogram((0, 0), "$\textbf{(A)}$", new int[] {3, 4, 4, 3, 4, 3, 4}); histogram((12, 0), "$\textbf{(B)}$", new int[] {3, 4, 4, 4, 3, 3, 4}); histogram((24, 0), "$\textbf{(C)}$", new int[] {3, 4, 4, 4, 4, 3, 3}); histogram((0, -8), "$\textbf{(D)}$", new int[] {4, 3, 4, 3, 4, 3, 4}); histogram((12, -8), "$\textbf{(E)}$", new int[] {4, 4, 3, 4, 3, 4, 3}); [/asy]](https://latex.artofproblemsolving.com/4/c/b/4cba093bf55b34f4838e00be60618cfcab45fd8f.png) Solution
Solution
Problem 14
A number ![]() is inserted into the list
is inserted into the list ![]() . The mean is now twice as great as the median. What is
. The mean is now twice as great as the median. What is ![]() ?
?
![]()
Problem 15
Kei draws a ![]() -by-
-by-![]() grid. He colors
grid. He colors ![]() of the unit squares silver and the remaining squares gold. Kei then folds the grid in half vertically, forming pairs of overlapping unit squares. Let
of the unit squares silver and the remaining squares gold. Kei then folds the grid in half vertically, forming pairs of overlapping unit squares. Let ![]() and
and ![]() equal the least and greatest possible number of gold-on-gold pairs, respectively. What is the value of
equal the least and greatest possible number of gold-on-gold pairs, respectively. What is the value of ![]() ?
?
![[asy] import graph; size(100); pen gridPen = black; void drawSquare(pair p) { draw(box(p, p + (1,1)), gridPen); } int[][] grid = { {1, 1, 1, 1, 1, 1}, {1, 1, 1, 1, 1, 1}, {1, 1, 1, 1, 1, 1}, {1, 1, 1, 1, 1, 1}, {1, 1, 1, 1, 1, 1}, {1, 1, 1, 1, 1, 1}, }; int rows = grid.length; int cols = grid[0].length; for (int i = 0; i < rows; ++i) { for (int j = 0; j < cols; ++j) { if (grid[i][j] == 1) { drawSquare((j, rows - i - 1)); } } } [/asy]](https://latex.artofproblemsolving.com/f/0/3/f0332c51783c0206497135bf92789f06be712b80.png)
![]()
Problem 16
Five distinct integers from ![]() to
to ![]() are chosen, and five distinct integers from
are chosen, and five distinct integers from ![]() to
to ![]() are chosen. No two numbers differ by exactly
are chosen. No two numbers differ by exactly ![]() . What is the sum of the ten chosen numbers?
. What is the sum of the ten chosen numbers?
![]()
Problem 17
In the land of Markovia, there are three cities: ![]() ,
, ![]() , and
, and ![]() . There are
. There are ![]() people who live in
people who live in ![]() ,
, ![]() who live in
who live in ![]() , and
, and ![]() who live in
who live in ![]() . Everyone works in one of the three cities, and a person may work in the same city where they live. In the figure below, an arrow pointing from one city to another is labeled with the fraction of people living in the first city who work in the second city. (For example,
. Everyone works in one of the three cities, and a person may work in the same city where they live. In the figure below, an arrow pointing from one city to another is labeled with the fraction of people living in the first city who work in the second city. (For example, ![]() of the people who live in
of the people who live in ![]() work in
work in ![]() .) How many people work in
.) How many people work in ![]() ?
?
![[asy] /* AMC8 P17 2025, by NUMANA: BUI VAN HIEU, buivanhieu@husc.edu.vn, https://husc.edu.vn, https://husc.edu.vn */ import graph; unitsize(2cm); real r=0.15; pair A, B, C;B = (0,0);C = (2,0);A = (1,sqrt(3)); // Drawing the nodes draw(circle(A,r)); label("$A$", A); draw(circle(B,r)); label("$B$", B); draw(circle(C,r)); label("$C$", C); guide AB=A+r*dir(-135)..{down}B+r*dir(90), BA=B+r*dir(60)..{up}A+r*dir(-105), BC=B+r*dir(0)..(1,-0.2)..C+r*dir(180), CB=C+r*dir(150)..(1,0.3)..B+r*dir(30), CA=C+r*dir(90){up}..A+r*dir(-45), AC=A+r*dir(-75){down}..C+r*dir(120); draw(AB,L=Label("$1/4$", MidPoint, W),Arrow(HookHead));draw(BA,L=Label("$1/3$", MidPoint, W),Arrow(HookHead));draw(BC,L=Label("$1/6$", MidPoint, S),Arrow(HookHead));draw(CB,L=Label("$1/10$", MidPoint, S),Arrow(HookHead)); draw(CA,L=Label("$1/8$", MidPoint, E),Arrow(HookHead));draw(AC,L=Label("$1/5$", MidPoint, E),Arrow(HookHead)); [/asy]](https://latex.artofproblemsolving.com/f/a/3/fa3fd1df2b4e0ab88475c2c120ce2384452be065.png)
![]()
Problem 18
The circle shown below on the left has a radius of 1 unit. The region between the circle and the inscribed square is shaded. In the circle shown on the right, one quarter of the region between the circle and the inscribed square is shaded. The shaded regions in the two circles have the same area. What is the radius ![]() , in units, of the circle on the right?
, in units, of the circle on the right?
![[asy] unitsize(40); real a = 0.707; fill(circle((a,a), 1), grey); fill((0,0)--(0,1.414)--(1.414,1.414)--(1.414,0)--cycle, white); draw((0,0)--(0,1.414)--(1.414,1.414)--(1.414,0)--cycle); draw(circle((a,a), 1)); draw((0.707,0.707)--(1.414,1.414)); dot((0.707,0.707)); label("$1$", (1,1), SE); fill(circle((4+a, a), 2*a), grey); fill(shift((4+a,a)) * ((-2,-2)--(1,-2)--(1,2)--(-2,2)--cycle), white); draw(shift((4+a,a)) * ((-1,-1)--(1,-1)--(1,1)--(-1,1)--cycle)); draw(circle((4+a, a), 2*a)); draw((4+a,a)--(5+a,1+a)); dot((4+a,a)); label("$R$", (a+4.5,a+0.5), SE); [/asy]](https://latex.artofproblemsolving.com/2/f/a/2fa4a55e3a7d0fba0d2897230e6c2fbbc47ae8f8.png)
![]()
Problem 19
Two towns, ![]() and
and ![]() , are connected by a straight road,
, are connected by a straight road, ![]() miles long. Traveling from town
miles long. Traveling from town ![]() to town
to town ![]() , the speed limit changes every
, the speed limit changes every ![]() miles: from
miles: from ![]() to
to ![]() to
to ![]() miles per hour (mph). Two cars, one at town
miles per hour (mph). Two cars, one at town ![]() and one at town
and one at town ![]() , start moving toward each other at the same time. They drive at exactly the speed limit in each portion of the road. How far from town
, start moving toward each other at the same time. They drive at exactly the speed limit in each portion of the road. How far from town ![]() , in miles, will the two cars meet?
, in miles, will the two cars meet?
![]()
Problem 20
Sarika, Dev, and Rajiv are sharing a large block of cheese. They take turns cutting off half of what remains and eating it: first Sarika eats half of the cheese, then Dev eats half of the remaining half, then Rajiv eats half of what remains, then back to Sarika, and so on. They stop when the cheese is too small to see. About what fraction of the original block of cheese does Sarika eat in total?
![]()
Problem 21
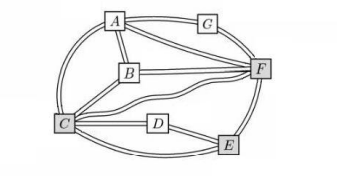
The Konigsberg School has assigned grades 1 through 7 to pods ![]() through
through ![]() , one grade per pod. Some of the pods are connected by walkways, as shown in the figure below. The school noticed that each pair of connected pods has been assigned grades differing by 2 or more grade levels. (For example, grades 1 and 2 will not be in pods directly connected by a walkway.) What is the sum of the grade levels assigned to pods
, one grade per pod. Some of the pods are connected by walkways, as shown in the figure below. The school noticed that each pair of connected pods has been assigned grades differing by 2 or more grade levels. (For example, grades 1 and 2 will not be in pods directly connected by a walkway.) What is the sum of the grade levels assigned to pods ![]() , and
, and ![]() ?
?
![]()
Problem 22
A classroom has a row of 35 coat hooks. Paulina likes coats to be equally spaced, so that there is the same number of empty hooks before the first coat, after the last coat, and between every coat and the next one. Suppose there is at least 1 coat and at least 1 empty hook. How many different numbers of coats can satisfy Paulina's pattern?
![]()
Problem 23
How many four-digit numbers have all three of the following properties?
(I) The tens and ones digit are both 9.
(II) The number is 1 less than a perfect square.
(III) The number is the product of exactly two prime numbers.
![]()
Problem 24
In trapezoid ![]() , angles
, angles ![]() and
and ![]() measure
measure ![]() and
and ![]() . The side lengths are all positive integers, and the perimeter of
. The side lengths are all positive integers, and the perimeter of ![]() is
is ![]() units. How many non-congruent trapezoids satisfy all of these conditions?
units. How many non-congruent trapezoids satisfy all of these conditions?
![]()
Problem 25
Makayla finds all the possible ways to draw a path in a ![]() diamond-shaped grid. Each path starts at the bottom of the grid and ends at the top, always moving one unit northeast or northwest. She computes the area of the region between each path and the right side of the grid. Two examples are shown in the figures below. What is the sum of the areas determined by all possible paths?
diamond-shaped grid. Each path starts at the bottom of the grid and ends at the top, always moving one unit northeast or northwest. She computes the area of the region between each path and the right side of the grid. Two examples are shown in the figures below. What is the sum of the areas determined by all possible paths?
![[asy] unitsize(9); real a = 0.7071; path w = (0,0)--(2a, 2a)--(-a,5a)--(a,7a)--(-a,9a)--(0,10a); fill(w--(5a,5a)--cycle, gray(0.8)); draw(w, linewidth(1.5)); path x = (10,0)--(10-a,a)--(10+2a,4a)--(10-2a,8a)--(10,10a); fill(x--(10+5a,5a)--cycle, gray(0.8)); draw(x, linewidth(1.5)); add(rotate(45, (0,0)) * grid(5,5)); add(rotate(45, (10,0)) * (shift((10,0)) * grid(5,5))); dot((0,0)); dot((0,7.07106)); dot((10,0)); dot((10,7.07106)); label("area = 11", (0,-1), S); label("area = 13", (10,-1), S); [/asy]](https://latex.artofproblemsolving.com/1/9/f/19f1befa81b8e426d1d05f6a7650b5b6a41b0e2f.png)
![]()