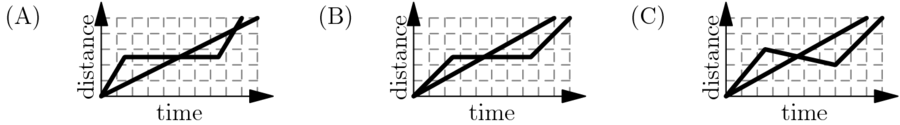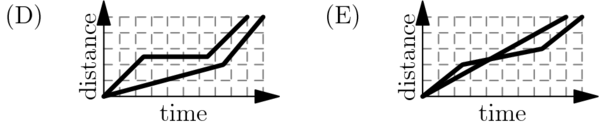2019년 11월 30일 토요일
2019 AMC 8 기하문제 해설
In triangle ABC, point D divides side AC so that AD : DC = 1 : 2.
Let E be the midpoint of BD and let F be the point of intersection of line BC
and line AE.
Given that the area of ABC is 360, what is the area of EBF ?
삼각형 ABC 에서 , D점이 AC를 AD : DC = 1 : 2 로 내분한다.
E 는 BD 의 중점이고, F는 BC 와 AE 의 교점이다.
삼각형 ABC 의 넓이는 360 이다. 삼각형 EBF 의 넓이는 얼마인가 ?
(A) 24 (B) 30 (C) 32 (D) 36 (E) 40
해설
점 F 와 점 D를 연결하여 보조선 FD 를 긋는다.
삼각형 ABD 삼각형 BCD 의 넓이는 전체넓이 360의 1 : 2 로
각각 120 과 240 이다.
삼각형 ABD 에서 E 는 BD 의 중점이니 ,
삼각형 ABE , 삼각형 ADE 의 넓이는 각각 60 이다.
삼각형 BDF 에서, 마찬가지로 삼각형 BEF 와 삼각형 DEF 의 넓이는
서로 같다.
삼각형 BEF 와 삼각형 DEF 의 넓이를 x 로 두자.
삼각형 CDF 의 넓이는 240-2x 가 된다.
삼각형 ABC 에서 BF : FC = (60 + x) : (300 - x) 가 된다.
삼각형 BCD 에서 BF : FC = 2x : 240 - 2x
즉 BF : FC = x : (120 - x) 이다.
삼각형 ABC 에서 BF : FC = (60 + x) : (300 - x) = x : (120 - x)
240 x = 7200
x = 30 이다
삼각형 EBF 의 넓이는 30 이다.
(추가 문제)
삼각형 ABC에서 AD : DC = 1 : 2 ,
BE : ED = 1 : 1 이다. BF : FC 는 몇대 몇 인가?
궁금한게 있거나, 모르는 부분이 있으면 연락 바랍니다.
010-3549-5206
2019년 11월 29일 금요일
대구 경북 WMTC 참가팀 각학년별 6명씩 모집합니다.
각학년별 6명씩을 뽑아 성대 KMC JKMO KMO AMC8/1012 AIME 등 대회를 준비하며, 수학적 방법을 터득하고 응용하여 국내외 수학경시나 올림피아드에 참가하고 수학을 통하여 세계각국의 친구들과 경쟁하고 좋은 친구들과 사귀며 훌륭한 인간관계를 맺을수 있는 좋은 기회의 장이 될수 있습니다.
대구 경북 지역의 초등 중등 고등 학생으로 수학에 자신있고 최고수준의 실력을 가진 친구들과 토의 하고 문제를 같이 풀며 새로운 문제에 도전하며 자기의 능력을 키울수 있게 된다면 좋을 것입니다,
수학에 재능이 있고 영재고 과학고 진학해서 장차 과학자 수학자가 꿈인 인재를 조기에 발굴하여 최고의 실력을 갗춘 인재로 키우려고 합니다. 국내 수학 경시대회를 포함한 전세계 수학 경시대회 참가할 인재양성을 목표로 어릴 때부터 수학적 방법, 수학의 아름다움을 느끼며, 즐겁게 수학 하고자 하는 인재를 구해 전심전력을 다해 가르치고자 합니다.
WMTC란?
World Mathematics Team Championship (이하 WMTC)는 6명이 한 팀이 되며
개인전, 단체전(팀라운드/릴레이라운드)의 성적이 합산되는 팀대회로
올해 10주년을 맞는 국제 수학 팀 대회입니다.
2015년까지 중국에서 대회가 진행되다 2016년에 한국에서 성공적으로 대회가 진행되었고 2017년 태국 (방콕), 2018년은 불가리아 (바르나)에서 대회가 진행되었으며 2019년 한국에서 대회가 진행됩니다.
저학년의 경우 상위 단계 참가가 가능 합니다.
AMC 8/10/12 미국수학경시대회 AIME
SCAT SSAT PSAT GED SATmath ACT
SCAT SSAT PSAT GED SATmath ACT
국제학교영어원서 강의 수학과학올림피아드
수학과학경시대회 성대 KMC KJMO KMO
교육청영재원 교대영재원 경대영재원 준비반 모집
상담 환영합니다
053-765-8233
010-3549-5206
2019년 11월 26일 화요일
2019 AMC8 문제 및 정답 안내
Problem 1
Ike and Mike go into a sandwich shop with a total of  to spend. Sandwiches cost
to spend. Sandwiches cost  each and soft drinks cost
each and soft drinks cost  each. Ike and Mike plan to buy as many sandwiches as they can and use the remaining money to buy soft drinks. Counting both soft drinks and sandwiches, how many items will they buy?
each. Ike and Mike plan to buy as many sandwiches as they can and use the remaining money to buy soft drinks. Counting both soft drinks and sandwiches, how many items will they buy?
Problem 2
Three identical rectangles are put together to form rectangle  , as shown in the figure below. Given that the length of the shorter side of each of the smaller rectangles is
, as shown in the figure below. Given that the length of the shorter side of each of the smaller rectangles is  feet, what is the area in square feet of rectangle
feet, what is the area in square feet of rectangle  ?
?
![[asy] draw((0,0)--(3,0)); draw((0,0)--(0,2)); draw((0,2)--(3,2)); draw((3,2)--(3,0)); dot((0,0)); dot((0,2)); dot((3,0)); dot((3,2)); draw((2,0)--(2,2)); draw((0,1)--(2,1)); label("A",(0,0),S); label("B",(3,0),S); label("C",(3,2),N); label("D",(0,2),N); [/asy]](https://latex.artofproblemsolving.com/e/0/7/e0752885e3cff488bd89893347c595b7c570d339.png)
Problem 3
Which of the following is the correct order of the fractions  ,
,  , and
, and  , from least to greatest?
, from least to greatest?
Problem 4
Quadrilateral  is a rhombus with perimeter
is a rhombus with perimeter  meters. The length of diagonal
meters. The length of diagonal  is
is  meters. What is the area in square meters of rhombus
meters. What is the area in square meters of rhombus  ?
?
![[asy] draw((-13,0)--(0,5)); draw((0,5)--(13,0)); draw((13,0)--(0,-5)); draw((0,-5)--(-13,0)); dot((-13,0)); dot((0,5)); dot((13,0)); dot((0,-5)); label("A",(-13,0),W); label("B",(0,5),N); label("C",(13,0),E); label("D",(0,-5),S); [/asy]](https://latex.artofproblemsolving.com/e/5/4/e54b35c6e9f6a1eaa16a3138ed06ebc73122be63.png)
Problem 5
A tortoise challenges a hare to a race. The hare eagerly agrees and quickly runs ahead, leaving the slow-moving tortoise behind. Confident that he will win, the hare stops to take a nap. Meanwhile, the tortoise walks at a slow steady pace for the entire race. The hare awakes and runs to the finish line, only to find the tortoise already there. Which of the following graphs matches the description of the race, showing the distance  traveled by the two animals over time
traveled by the two animals over time  from start to finish?
from start to finish?
Problem 6
There are  grid points (uniformly spaced) in the square shown in the diagram below, including the points on the edges. Point
grid points (uniformly spaced) in the square shown in the diagram below, including the points on the edges. Point  is in the center of the square. Given that point
is in the center of the square. Given that point  is randomly chosen among the other
is randomly chosen among the other  points, what is the probability that the line
points, what is the probability that the line  is a line of symmetry for the square?
is a line of symmetry for the square?
![[asy] draw((0,0)--(0,8)); draw((0,8)--(8,8)); draw((8,8)--(8,0)); draw((8,0)--(0,0)); dot((0,0)); dot((0,1)); dot((0,2)); dot((0,3)); dot((0,4)); dot((0,5)); dot((0,6)); dot((0,7)); dot((0,8)); dot((1,0)); dot((1,1)); dot((1,2)); dot((1,3)); dot((1,4)); dot((1,5)); dot((1,6)); dot((1,7)); dot((1,8)); dot((2,0)); dot((2,1)); dot((2,2)); dot((2,3)); dot((2,4)); dot((2,5)); dot((2,6)); dot((2,7)); dot((2,8)); dot((3,0)); dot((3,1)); dot((3,2)); dot((3,3)); dot((3,4)); dot((3,5)); dot((3,6)); dot((3,7)); dot((3,8)); dot((4,0)); dot((4,1)); dot((4,2)); dot((4,3)); dot((4,4)); dot((4,5)); dot((4,6)); dot((4,7)); dot((4,8)); dot((5,0)); dot((5,1)); dot((5,2)); dot((5,3)); dot((5,4)); dot((5,5)); dot((5,6)); dot((5,7)); dot((5,8)); dot((6,0)); dot((6,1)); dot((6,2)); dot((6,3)); dot((6,4)); dot((6,5)); dot((6,6)); dot((6,7)); dot((6,8)); dot((7,0)); dot((7,1)); dot((7,2)); dot((7,3)); dot((7,4)); dot((7,5)); dot((7,6)); dot((7,7)); dot((7,8)); dot((8,0)); dot((8,1)); dot((8,2)); dot((8,3)); dot((8,4)); dot((8,5)); dot((8,6)); dot((8,7)); dot((8,8)); label("P",(4,4),NE); [/asy]](https://latex.artofproblemsolving.com/2/e/f/2ef50880b9e105fcb40568742659a26c359c6c1a.png)
Problem 7
Shauna takes five tests, each worth a maximum of  points. Her scores on the first three tests are
points. Her scores on the first three tests are  ,
,  , and
, and  . In order to average
. In order to average  for all five tests, what is the lowest score she could earn on one of the other two tests?
for all five tests, what is the lowest score she could earn on one of the other two tests?
Problem 8
Gilda has a bag of marbles. She gives  of them to her friend Pedro. Then Gilda gives
of them to her friend Pedro. Then Gilda gives  of what is left to another friend, Ebony. Finally, Gilda gives
of what is left to another friend, Ebony. Finally, Gilda gives  of what is now left in the bag to her brother Jimmy. What percentage of her original bag of marbles does Gilda have left for herself?
of what is now left in the bag to her brother Jimmy. What percentage of her original bag of marbles does Gilda have left for herself?
Problem 9
Alex and Felicia each have cats as pets. Alex buys cat food in cylindrical cans that are  cm in diameter and
cm in diameter and  cm high. Felicia buys cat food in cylindrical cans that are
cm high. Felicia buys cat food in cylindrical cans that are  cm in diameter and
cm in diameter and  cm high. What is the ratio of the volume one of Alex's cans to the volume one of Felicia's cans?
cm high. What is the ratio of the volume one of Alex's cans to the volume one of Felicia's cans?
Problem 10
The diagram shows the number of students at soccer practice each weekday during last week. After computing the mean and median values, Coach discovers that there were actually  participants on Wednesday. Which of the following statements describes the change in the mean and median after the correction is made?
participants on Wednesday. Which of the following statements describes the change in the mean and median after the correction is made?![[asy] unitsize(2mm); defaultpen(fontsize(8bp)); real d = 5; real t = 0.7; real r; int[] num = {20,26,16,22,16}; string[] days = {"Monday","Tuesday","Wednesday","Thursday","Friday"}; for (int i=0; i<30; i=i+2) { draw((i,0)--(i,-5*d),gray); }for (int i=0; i<5; ++i) { r = -1*(i+0.5)*d; fill((0,r-t)--(0,r+t)--(num[i],r+t)--(num[i],r-t)--cycle,gray); label(days[i],(-1,r),W); }for(int i=0; i<32; i=i+4) { label(string(i),(i,1)); }label("Number of students at soccer practice",(14,3.5)); [/asy]](https://latex.artofproblemsolving.com/e/1/7/e1796ef723acbb9a4cfeacf57e69202cddf3e0d3.png)
![[asy] unitsize(2mm); defaultpen(fontsize(8bp)); real d = 5; real t = 0.7; real r; int[] num = {20,26,16,22,16}; string[] days = {"Monday","Tuesday","Wednesday","Thursday","Friday"}; for (int i=0; i<30; i=i+2) { draw((i,0)--(i,-5*d),gray); }for (int i=0; i<5; ++i) { r = -1*(i+0.5)*d; fill((0,r-t)--(0,r+t)--(num[i],r+t)--(num[i],r-t)--cycle,gray); label(days[i],(-1,r),W); }for(int i=0; i<32; i=i+4) { label(string(i),(i,1)); }label("Number of students at soccer practice",(14,3.5)); [/asy]](https://latex.artofproblemsolving.com/e/1/7/e1796ef723acbb9a4cfeacf57e69202cddf3e0d3.png)
Problem 11
The eighth grade class at Lincoln Middle School has  students. Each student takes a math class or a foreign language class or both. There are
students. Each student takes a math class or a foreign language class or both. There are  eighth graders taking a math class, and there are
eighth graders taking a math class, and there are  eight graders taking a foreign language class. How many eight graders take only a math class and not a foreign language class?
eight graders taking a foreign language class. How many eight graders take only a math class and not a foreign language class?
Problem 12
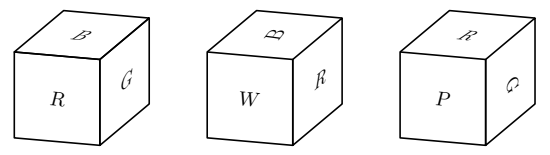
The faces of a cube are painted in six different colors: red  , white
, white  , green
, green  , brown
, brown  , aqua
, aqua  , and purple
, and purple  . Three views of the cube are shown below. What is the color of the face opposite the aqua face?
. Three views of the cube are shown below. What is the color of the face opposite the aqua face?
Problem 13
A palindrome is a number that has the same value when read from left to right or from right to left. (For example, 12321 is a palindrome.) Let  be the least three-digit integer which is not a palindrome but which is the sum of three distinct two-digit palindromes. What is the sum of the digits of
be the least three-digit integer which is not a palindrome but which is the sum of three distinct two-digit palindromes. What is the sum of the digits of  ?
?
Problem 14
Isabella has  coupons that can be redeemed for free ice cream cones at Pete's Sweet Treats. In order to make the coupons last, she decides that she will redeem one every
coupons that can be redeemed for free ice cream cones at Pete's Sweet Treats. In order to make the coupons last, she decides that she will redeem one every  days until she has used them all. She knows that Pete's is closed on Sundays, but as she circles the
days until she has used them all. She knows that Pete's is closed on Sundays, but as she circles the  dates on her calendar, she realizes that no circled date falls on a Sunday. On what day of the week does Isabella redeem her first coupon?
dates on her calendar, she realizes that no circled date falls on a Sunday. On what day of the week does Isabella redeem her first coupon?
Problem 15
On a beach  people are wearing sunglasses and
people are wearing sunglasses and  people are wearing caps. Some people are wearing both sunglasses and caps. If one of the people wearing a cap is selected at random, the probability that this person is is also wearing sunglasses is
people are wearing caps. Some people are wearing both sunglasses and caps. If one of the people wearing a cap is selected at random, the probability that this person is is also wearing sunglasses is  . If instead, someone wearing sunglasses is selected at random, what is the probability that this person is also wearing a cap?
. If instead, someone wearing sunglasses is selected at random, what is the probability that this person is also wearing a cap?
Problem 16
Qiang drives  miles at an average speed of
miles at an average speed of  miles per hour. How many additional miles will he have to drive at
miles per hour. How many additional miles will he have to drive at  miles per hour to average
miles per hour to average  miles per hour for the entire trip?
miles per hour for the entire trip?
Problem 17
What is the value of the product![\[\left(\frac{1\cdot3}{2\cdot2}\right)\left(\frac{2\cdot4}{3\cdot3}\right)\left(\frac{3\cdot5}{4\cdot4}\right)\cdots\left(\frac{97\cdot99}{98\cdot98}\right)\left(\frac{98\cdot100}{99\cdot99}\right)?\]](https://latex.artofproblemsolving.com/9/c/a/9ca55aef127eee6fc870173ae1b23e1abd56a02b.png)
Problem 18
The faces of each of two fair dice are numbered  ,
,  ,
,  ,
,  ,
,  , and
, and  . When the two dice are tossed, what is the probability that their sum will be an even number?
. When the two dice are tossed, what is the probability that their sum will be an even number?
Problem 19
In a tournament there are six teams that play each other twice. A team earns  points for a win,
points for a win,  point for a draw, and
point for a draw, and  points for a loss. After all the games have been played it turns out that the top three teams earned the same number of total points. What is the greatest possible number of total points for each of the top three teams?
points for a loss. After all the games have been played it turns out that the top three teams earned the same number of total points. What is the greatest possible number of total points for each of the top three teams?
Problem 20
How many different real numbers  satisfy the equation
satisfy the equation![\[(x^{2}-5)^{2}=16?\]](https://latex.artofproblemsolving.com/d/1/8/d188c4697f3f7cf1889796a037bd60b6dae3b29e.png)
Problem 21
What is the area of the triangle formed by the lines  ,
,  , and
, and  ?
?
Problem 22
A store increased the original price of a shirt by a certain percent and then decreased the new price by the same amount. Given that the resulting price was  of the original price, by what percent was the price increased and decreased?
of the original price, by what percent was the price increased and decreased?
Problem 23
After Euclid High School's last basketball game, it was determined that  of the team's points were scored by Alexa and
of the team's points were scored by Alexa and  were scored by Brittany. Chelsea scored
were scored by Brittany. Chelsea scored  points. None of the other
points. None of the other  team members scored more than
team members scored more than  points. What was the total number of points scored by the other
points. What was the total number of points scored by the other  team members?
team members?
Problem 24
In triangle  , point
, point  divides side
divides side  so that
so that  . Let
. Let  be the midpoint of
be the midpoint of  and let
and let  be the point of intersection of line
be the point of intersection of line  and line
and line  . Given that the area of
. Given that the area of  is
is  , what is the area of
, what is the area of  ?
?
![[asy] unitsize(2cm); pair A,B,C,DD,EE,FF; B = (0,0); C = (3,0); A = (1.2,1.7); DD = (2/3)*A+(1/3)*C; EE = (B+DD)/2; FF = intersectionpoint(B--C,A--A+2*(EE-A)); draw(A--B--C--cycle); draw(A--FF); draw(B--DD);dot(A); label("$A$",A,N); dot(B); label("$B$", B,SW);dot(C); label("$C$",C,SE); dot(DD); label("$D$",DD,NE); dot(EE); label("$E$",EE,NW); dot(FF); label("$F$",FF,S); [/asy]](https://latex.artofproblemsolving.com/c/f/5/cf5d315e13b9e158a6df354d7f9a8ecafaf2b131.png)
Problem 25
Alice has  apples. In how many ways can she share them with Becky and Chris so that each of the people has at least
apples. In how many ways can she share them with Becky and Chris so that each of the people has at least  apples?
apples?
AOPS
파일이 첨부되어 있습니다.
2019-Problems-AMC8_final.pdf (847,777 byte)
2019년 11월 13일 시행된 AMC8 성적 결과는 12월 13일 금요일 저녁 6시 이후 공지됩니다.
1. D
2. E
3. E
4. D
5. B
6. C
7. A
8. E
9. B
10. B
11. D
12. A
13. A
14. C
15. B
16. D
17. B
18. C
19. C
20. D
21. E
22. E
23. B
24. B
25. C
2. E
3. E
4. D
5. B
6. C
7. A
8. E
9. B
10. B
11. D
12. A
13. A
14. C
15. B
16. D
17. B
18. C
19. C
20. D
21. E
22. E
23. B
24. B
25. C
피드 구독하기:
글 (Atom)