녹원학원 수학과학영재교육 010-3549-5206 : Pythagorean theorem 피타고라스의 정리

2013년 11월 18일 월요일

Pythagorean theorem 피타고라스의 정리

In mathematics, the Pythagorean theorem—or Pythagoras' theorem—is a relation in Euclidean geometry among the three sides of a right triangle. It states that the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides. The theorem can be written as an equation relating the lengths of the sides a, b and c, often called the Pythagorean equation:^[1]

$a^2 + b^2 = c^2\!\,$

where c represents the length of the hypotenuse, and a and b represent the lengths of the other two sides.

The Pythagorean theorem is named after the Greek mathematician Pythagoras (ca. 570 BC—ca. 495 BC), who by tradition is credited with its proof,^[2]^[3] although it is often argued that knowledge of the theorem predates him. There is evidence that Babylonian mathematicians understood the formula, although there is little surviving evidence that they used it in a mathematical framework.^[4]^[5] Also, Mesopotamian, Indian and Chinese mathematicians have all been known for independently discovering the result, some even providing proofs of special cases.

The theorem has numerous proofs, possibly the most of any mathematical theorem. These are very diverse, including both geometric proofs and algebraic proofs, with some dating back thousands of years. The theorem can be generalized in various ways, including higher-dimensional spaces, to spaces that are not Euclidean, to objects that are not right triangles, and indeed, to objects that are not triangles at all, but n-dimensional solids. The Pythagorean theorem has attracted interest outside mathematics as a symbol of mathematical abstruseness, mystique, or intellectual power; popular references in literature, plays, musicals, songs, stamps and cartoons abound.

[hide]

Pythagorean proof

The Pythagorean proof

The Pythagorean Theorem was known long before Pythagoras, but he may well have been the first to prove it.^[6] In any event, the proof attributed to him is very simple, and is called a proof by rearrangement.

The two large squares shown in the figure each contain four identical triangles, and the only difference between the two large squares is that the triangles are arranged differently. Therefore, the white space within each of the two large squares must have equal area. Equating the area of the white space yields the Pythagorean Theorem, Q.E.D.^[7]

That Pythagoras originated this very simple proof is sometimes inferred from the writings of the later Greek philosopher and mathematician Proclus.^[8] Several other proofs of this theorem are described below, but this is known as the Pythagorean one.

Other forms of the theorem

As pointed out in the introduction, if c denotes the length of the hypotenuse and a and b denote the lengths of the other two sides, the Pythagorean theorem can be expressed as the Pythagorean equation:

$a^2 + b^2 = c^2\,$ If the length of both a and b are known, then c can be calculated as follows:

$c = \sqrt{a^2 + b^2}. \,$

If the length of hypotenuse c and one leg (a or b) are known, then the length of the other leg can be calculated with the following equations:

$a = \sqrt{c^2 - b^2}. \,$

$b = \sqrt{c^2 - a^2}. \,$

The Pythagorean equation relates the sides of a right triangle in a simple way, so that if the lengths of any two sides are known the length of the third side can be found. Another corollary of the theorem is that in any right triangle, the hypotenuse is greater than any one of the legs, but less than the sum of them.

A generalization of this theorem is the law of cosines, which allows the computation of the length of the third side of any triangle, given the lengths of two sides and the size of the angle between them. If the angle between the sides is a right angle, the law of cosines reduces to the Pythagorean equation.

Other proofs of the theorem

This theorem may have more known proofs than any other (the law of quadratic reciprocity being another contender for that distinction); the book The Pythagorean Proposition contains 370 proofs.^[9]

Proof using similar triangles

This proof is based on the proportionality of the sides of two similar triangles, that is, upon the fact that the ratio of any two corresponding sides of similar triangles is the same regardless of the size of the triangles.

Let ABC represent a right triangle, with the right angle located at C, as shown on the figure. We draw the altitude from point C, and call H its intersection with the side AB. Point H divides the length of the hypotenuse c into parts d and e. The new triangle ACH is similar to triangle ABC, because they both have a right angle (by definition of the altitude), and they share the angle at A, meaning that the third angle will be the same in both triangles as well, marked as θ in the figure. By a similar reasoning, the triangle CBH is also similar to ABC. The proof of similarity of the triangles requires the Triangle postulate: the sum of the angles in a triangle is two right angles, and is equivalent to the parallel postulate. Similarity of the triangles leads to the equality of ratios of corresponding sides:

$\frac{BC}{AB}=\frac{BH}{BC} \text{ and } \frac{AC}{AB}=\frac{AH}{AC}.\,$

The first result equates the cosine of each angle θ and the second result equates the sines.

These ratios can be written as:

${BC}^{2}={AB}\times {BH} \text{ and }{AC}^{2}={AB}\times {AH}. \,$

Summing these two equalities, we obtain

${BC}^{2}+{AC}^{2}={AB}\times {BH}+{AB}\times {AH}={AB}\times({AH}+{BH})={AB}^{2} ,\,\!$

which, tidying up, is the Pythagorean theorem:

${BC}^{2}+{AC}^{2}={AB}^{2} \ .\,\!$

The role of this proof in history is the subject of much speculation. The underlying question is why Euclid did not use this proof, but invented another. One conjecture is that the proof by similar triangles involved a theory of proportions, a topic not discussed until later in the Elements, and that the theory of proportions needed further development at that time.^[10]^[11]

Euclid's proof

Proof in Euclid's Elements

In outline, here is how the proof in Euclid's Elements proceeds. The large square is divided into a left and right rectangle. A triangle is constructed that has half the area of the left rectangle. Then another triangle is constructed that has half the area of the square on the left-most side. These two triangles are shown to be congruent, proving this square has the same area as the left rectangle. This argument is followed by a similar version for the right rectangle and the remaining square. Putting the two rectangles together to reform the square on the hypotenuse, its area is the same as the sum of the area of the other two squares. The details are next.

Let A, B, C be the vertices of a right triangle, with a right angle at A. Drop a perpendicular from A to the side opposite the hypotenuse in the square on the hypotenuse. That line divides the square on the hypotenuse into two rectangles, each having the same area as one of the two squares on the legs.

For the formal proof, we require four elementary lemmata:

If two triangles have two sides of the one equal to two sides of the other, each to each, and the angles included by those sides equal, then the triangles are congruent (side-angle-side).
The area of a triangle is half the area of any parallelogram on the same base and having the same altitude.
The area of a rectangle is equal to the product of two adjacent sides.
The area of a square is equal to the product of two of its sides (follows from 3).

Next, each top square is related to a triangle congruent with another triangle related in turn to one of two rectangles making up the lower square.^[12]

Illustration including the new lines

Showing the two congruent triangles of half the area of rectangle BDLK and square BAGF

The proof is as follows:

Let ACB be a right-angled triangle with right angle CAB.
On each of the sides BC, AB, and CA, squares are drawn, CBDE, BAGF, and ACIH, in that order. The construction of squares requires the immediately preceding theorems in Euclid, and depends upon the parallel postulate.^[13]
From A, draw a line parallel to BD and CE. It will perpendicularly intersect BC and DE at K and L, respectively.
Join CF and AD, to form the triangles BCF and BDA.
Angles CAB and BAG are both right angles; therefore C, A, and G are collinear. Similarly for B, A, and H.
Angles CBD and FBA are both right angles; therefore angle ABD equals angle FBC, since both are the sum of a right angle and angle ABC.
Since AB is equal to FB and BD is equal to BC, triangle ABD must be congruent to triangle FBC.
Since A-K-L is a straight line, parallel to BD, then rectangle BDLK has twice the area of triangle ABD because they share the base BD and have the same altitude BK, i.e., a line normal to their common base, connecting the parallel lines BD and AL. (lemma 2)
Since C is collinear with A and G, square BAGF must be twice in area to triangle FBC.
Therefore rectangle BDLK must have the same area as square BAGF = AB².
Similarly, it can be shown that rectangle CKLE must have the same area as square ACIH = AC².
Adding these two results, AB² + AC² = BD × BK + KL × KC
Since BD = KL, BD × BK + KL × KC = BD(BK + KC) = BD × BC
Therefore AB² + AC² = BC², since CBDE is a square.

This proof, which appears in Euclid's Elements as that of Proposition 47 in Book 1,^[14] demonstrates that the area of the square on the hypotenuse is the sum of the areas of the other two squares.^[15] This is quite distinct from the proof by similarity of triangles, which is conjectured to be the proof that Pythagoras used.^[11]^[16]

Proof by rearrangement

We have already discussed the Pythagorean proof, which was a proof by rearrangement. The same idea is conveyed by the leftmost animation below, which consists of a large square, side a + b, containing four identical right triangles. The triangles are shown in two arrangements, the first of which leaves two squares a² and b² uncovered, the second of which leaves square c² uncovered. The area encompassed by the outer square never changes, and the area of the four triangles is the same at the beginning and the end, so the black square areas must be equal, therefore a² + b² = c².

A second proof by rearrangement is given by the middle animation. A large square is formed with area c², from four identical right triangles with sides a, b and c, fitted around a small central square. Then two rectangles are formed with sides a and b by moving the triangles. Combining the smaller square with these rectangles produces two squares of areas a² and b², which must have the same area as the initial large square.^[17]

The third, rightmost image also gives a proof. The upper two squares are divided as shown by the blue and green shading, into pieces that when rearranged can be made to fit in the lower square on the hypotenuse – or conversely the large square can be divided as shown into pieces that fill the other two. This shows the area of the large square equals that of the two smaller ones.^[18]

Animation showing proof by rearrangement of four identical right triangles

Animation showing another proof by rearrangement

Proof using an elaborate rearrangement

Algebraic proofs

Diagram of the two algebraic proofs

The theorem can be proved algebraically using four copies of a right triangle with sides a, b and c, arranged inside a square with side c as in the top half of the diagram.^[19] The triangles are similar with area $\tfrac12ab$ , while the small square has side b − a and area (b − a)². The area of the large square is therefore

$(b-a)^2+4\frac{ab}{2} = (b-a)^2+2ab = a^2+b^2. \,$

But this is a square with side c and area c², so

$c^2 = a^2 + b^2. \,$

A similar proof uses four copies of the same triangle arranged symmetrically around a square with side c, as shown in the lower part of the diagram.^[20] This results in a larger square, with side a + b and area (a + b)². The four triangles and the square side c must have the same area as the larger square,

$(b+a)^2 = c^2 + 4\frac{ab}{2} = c^2+2ab,\,$

giving

$c^2 = (b+a)^2 - 2ab = a^2 + b^2.\,$

Diagram of Garfield's proof

A related proof was published by future U.S. President James A. Garfield (then a U.S. Representative).^[21]^[22] Instead of a square it uses a trapezoid, which can be constructed from the square in the second of the above proofs by bisecting along a diagonal of the inner square, to give the trapezoid as shown in the diagram. The area of the trapezoid can be calculated to be half the area of the square, that is

$\frac{1}{2}(b+a)^2.$

The inner square is similarly halved, and there are only two triangles so the proof proceeds as above except for a factor of $\frac{1}{2}$ , which is removed by multiplying by two to give the result.

Proof using differentials

One can arrive at the Pythagorean theorem by studying how changes in a side produce a change in the hypotenuse and employing calculus.^[23]^[24]^[25]
The triangle ABC is a right triangle, as shown in the upper part of the diagram, with BC the hypotenuse. At the same time the triangle lengths are measured as shown, with the hypotenuse of length y, the side AC of length x and the side AB of length a, as seen in the lower diagram part.

Diagram for differential proof

If x is increased by a small amount dx by extending the side AC slightly to D, then y also increases by dy. These form two sides of a triangle, CDE, which (with E chosen so CE is perpendicular to the hypotenuse) is a right triangle approximately similar to ABC. Therefore the ratios of their sides must be the same, that is:

$\frac{dy}{dx} = \frac xy.$
This can be rewritten as follows:

$y \cdot dy - x \cdot dx = 0.\,$

This is a differential equation which is solved to give

$y^2 - x^2 = C,\,$
And the constant can be deduced from x = 0, y = a to give the equation

$y^2 = x^2 + a^2\,$
This is more of an intuitive proof than a formal one: it can be made more rigorous if proper limits are used in place of dx and dy.

Converse

The converse of the theorem is also true:^[26]

For any three positive numbers a, b, and c such that a² + b² = c², there exists a triangle with sides a, b and c, and every such triangle has a right angle between the sides of lengths a and b.
An alternative statement is:

For any triangle with sides a, b, c, if a² + b² = c², then the angle between a and b measures 90°.

This converse also appears in Euclid's Elements (Book I, Proposition 48):^[27]

"If in a triangle the square on one of the sides equals the sum of the squares on the remaining two sides of the triangle, then the angle contained by the remaining two sides of the triangle is right."

It can be proven using the law of cosines or as follows:

Let ABC be a triangle with side lengths a, b, and c, with a² + b² = c². Construct a second triangle with sides of length a and b containing a right angle. By the Pythagorean theorem, it follows that the hypotenuse of this triangle has length c = √a² + b², the same as the hypotenuse of the first triangle. Since both triangles' sides are the same lengths a, b and c, the triangles are congruent and must have the same angles. Therefore, the angle between the side of lengths a and b in the original triangle is a right angle.

The above proof of the converse makes use of the Pythagorean Theorem itself. The converse can also be proven without assuming the Pythagorean Theorem.^[28]^[29]

A corollary of the Pythagorean theorem's converse is a simple means of determining whether a triangle is right, obtuse, or acute, as follows. Let c be chosen to be the longest of the three sides and a + b > c (otherwise there is no triangle according to the triangle inequality). The following statements apply:^[30]

If a² + b² = c², then the triangle is right.
If a² + b² > c², then the triangle is acute.
If a² + b² < c², then the triangle is obtuse.

Edsger Dijkstra has stated this proposition about acute, right, and obtuse triangles in this language:

sgn(α + β − γ) = sgn(a² + b² − c²),

where α is the angle opposite to side a, β is the angle opposite to side b, γ is the angle opposite to side c, and sgn is the sign function.^[31]

Consequences and uses of the theorem

Pythagorean triples

Main article: Pythagorean triple

A Pythagorean triple has three positive integers a, b, and c, such that a² + b² = c². In other words, a Pythagorean triple represents the lengths of the sides of a right triangle where all three sides have integer lengths.^[1] Evidence from megalithic monuments in Northern Europe shows that such triples were known before the discovery of writing. Such a triple is commonly written (a, b, c). Some well-known examples are (3, 4, 5) and (5, 12, 13).

A primitive Pythagorean triple is one in which a, b and c are coprime (the greatest common divisor of a, b and c is 1).
The following is a list of primitive Pythagorean triples with values less than 100:

(3, 4, 5), (5, 12, 13), (7, 24, 25), (8, 15, 17), (9, 40, 41), (11, 60, 61), (12, 35, 37), (13, 84, 85), (16, 63, 65), (20, 21, 29), (28, 45, 53), (33, 56, 65), (36, 77, 85), (39, 80, 89), (48, 55, 73), (65, 72, 97)

Incommensurable lengths

The spiral of Theodorus: A construction for line segments with lengths whose ratios are the square root of a positive integer

One of the consequences of the Pythagorean theorem is that line segments whose lengths are incommensurable (so the ratio of which is not a rational number) can be constructed using a straightedge and compass. Pythagoras' theorem enables construction of incommensurable lengths because the hypotenuse of a triangle is related to the sides by the square root operation.

The figure on the right shows how to construct line segments whose lengths are in the ratio of the square root of any positive integer.^[32] Each triangle has a side (labeled "1") that is the chosen unit for measurement. In each right triangle, Pythagoras' theorem establishes the length of the hypotenuse in terms of this unit. If a hypotenuse is related to the unit by the square root of a positive integer that is not a perfect square, it is a realization of a length incommensurable with the unit, such as √2, √3, √5 . For more detail, see Quadratic irrational.

Incommensurable lengths conflicted with the Pythagorean school's concept of numbers as only whole numbers. The Pythagorean school dealt with proportions by comparison of integer multiples of a common subunit.^[33] According to one legend, Hippasus of Metapontum (ca. 470 B.C.) was drowned at sea for making known the existence of the irrational or incommensurable.^[34]^[35]

Complex numbers

The absolute value of a complex number z is the distance r from z to the origin

For any complex number

$z = x + iy,\,$

the absolute value or modulus is given by

$r = |z|=\sqrt{x^2 + y^2}.\,$

So the three quantities, r, x and y are related by the Pythagorean equation,

$r^2 = x^2 + y^2.\,$

Note that r is defined to be a positive number or zero but x and y can be negative as well as positive. Geometrically r is the distance of the z from zero or the origin O in the complex plane.

This can be generalised to find the distance between two points, z₁ and z₂ say. The required distance is given by

$|z_1 - z_2|=\sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2},\,$

so again they are related by a version of the Pythagorean equation,

$|z_1 - z_2|^2 = (x_1 - x_2)^2 + (y_1 - y_2)^2.\,$

Euclidean distance in various coordinate systems

The distance formula in Cartesian coordinates is derived from the Pythagorean theorem.^[36] If (x₁, y₁) and (x₂, y₂) are points in the plane, then the distance between them, also called the Euclidean distance, is given by

$\sqrt{(x_1-x_2)^2 + (y_1-y_2)^2}.$

More generally, in Euclidean n-space, the Euclidean distance between two points, $A\,=\,(a_1,a_2,\dots,a_n)$ and $B\,=\,(b_1,b_2,\dots,b_n)$ , is defined, by generalization of the Pythagorean theorem, as:

$\sqrt{(a_1-b_1)^2 + (a_2-b_2)^2 + \cdots + (a_n-b_n)^2} = \sqrt{\sum_{i=1}^n (a_i-b_i)^2}.$

If Cartesian coordinates are not used, for example, if polar coordinates are used in two dimensions or,

in more general terms, if curvilinear coordinates are used, the formulas expressing the Euclidean distance are more complicated than the Pythagorean theorem, but can be derived from it. A typical example where the straight-line distance between two points is converted to curvilinear coordinates can be found in the applications of Legendre polynomials in physics. The formulas can be discovered by using Pythagoras' theorem with the equations relating the curvilinear coordinates to Cartesian coordinates. For example, the polar coordinates (r, θ) can be introduced as:

$x = r \cos \theta, \ y = r \sin \theta.\,$

Then two points with locations (r₁, θ₁) and (r₂, θ₂) are separated by a distance s:

$s^2 = (x_1 - x_2)^2 + (y_1-y_2)^2 = (r_1 \cos \theta_1 -r_2 \cos \theta_2 )^2 + (r_1 \sin \theta_1 -r_2 \sin \theta_2)^2.\,$

Performing the squares and combining terms, the Pythagorean formula for distance in Cartesian coordinates produces the separation in polar coordinates as:

$\begin{align}s^2 &= r_1^2 +r_2^2 -2 r_1 r_2 \left( \cos \theta_1 \cos \theta_2 +\sin \theta_1 \sin \theta_2 \right)\\ &= r_1^2 +r_2^2 -2 r_1 r_2 \cos \left( \theta_1 - \theta_2\right)\\ &=r_1^2 +r_2^2 -2 r_1 r_2 \cos \Delta \theta \end{align} \ ,$

using the trigonometric product-to-sum formulas. This formula is the law of cosines, sometimes called the Generalized Pythagorean Theorem.^[37] From this result, for the case where the radii to the two locations are at right angles, the enclosed angle Δθ = π/2, and the form corresponding to Pythagoras' theorem is regained: $s^2 = r_1^2 + r_2^2.\,$ The Pythagorean theorem, valid for right triangles, therefore is a special case of the more general law of cosines, valid for arbitrary triangles.

Pythagorean trigonometric identity

Main article: Pythagorean trigonometric identity

Similar right triangles showing sine and cosine of angle θ

In a right triangle with sides a, b and hypotenuse c, trigonometry determines the sine and cosine of the angle θ between side a and the hypotenuse as:

$\sin \theta = \frac{b}{c}, \quad \cos \theta = \frac{a}{c}.$

From that it follows:

${\cos}^2 \theta + {\sin}^2 \theta = \frac{a^2 + b^2}{c^2} = 1,$

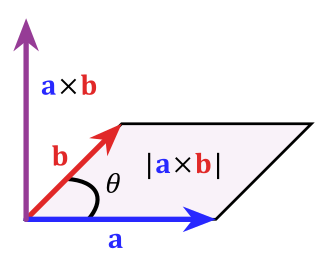
where the last step applies Pythagoras' theorem. This relation between sine and cosine sometimes is called the fundamental Pythagorean trigonometric identity.^[38] In similar triangles, the ratios of the sides are the same regardless of the size of the triangles, and depend upon the angles. Consequently, in the figure, the triangle with hypotenuse of unit size has opposite side of size sin θ and adjacent side of size cos θ in units of the hypotenuse.

Relation to the cross product

The area of a parallelogram as a cross product; vectors a and b identify a plane and a × b is normal to this plane.

The Pythagorean theorem relates the cross product and dot product in a similar way:^[39]

$\|\mathbf{a} \times \mathbf{b}\|^2 + (\mathbf{a} \cdot \mathbf{b})^2 = \|\mathbf{a}\|^2 \|\mathbf{b}\|^2\,$

This can be seen from the definitions of the cross product and dot product, as

$\begin{align} \mathbf{a} \times \mathbf{b} &= ab \mathbf{n} \sin{\theta} \\ \mathbf{a} \cdot \mathbf{b} &= ab \cos{\theta}\end{align}$

with n a unit vector normal to both a and b. The relationship follows from these definitions and the Pythagorean trigonometric identity.

This can also be used to define the cross product. By rearranging the following equation is obtained

$\|\mathbf{a} \times \mathbf{b}\|^2 = \|\mathbf{a}\|^2 \|\mathbf{b}\|^2 - (\mathbf{a} \cdot \mathbf{b})^2\,$

This can be considered as a condition on the cross product and so part of its definition, for example in seven dimensions.^[40]^[41]

Generalizations

Similar figures on the three sides

A generalization of the Pythagorean theorem extending beyond the areas of squares on the three sides to similar figures was known by Hippocrates of Chios in the fifth century BC,^[42] and was included by Euclid in his Elements:^[43]

If one erects similar figures (see Euclidean geometry) with corresponding sides on the sides of a right triangle, then the sum of the areas of the ones on the two smaller sides equals the area of the one on the larger side.

This extension assumes that the sides of the original triangle are the corresponding sides of the three congruent figures (so the common ratios of sides between the similar figures are a:b:c.^[44] While Euclid's proof only applied to convex polygons, the theorem also applies to concave polygons and even to similar figures that have curved boundaries (but still with part of a figure's boundary being the side of the original triangle).^[44]

The basic idea behind this generalization is that the area of a plane figure is proportional to the square of any linear dimension, and in particular is proportional to the square of the length of any side. Thus, if similar figures with areas A, B and C are erected on sides with corresponding lengths a, b and c then:

$\frac{A}{a^2} = \frac{B}{b^2} = \frac{C}{c^2}\, ,$

$\Rightarrow A + B = \frac{a^2}{c^2}C + \frac{b^2}{c^2}C\, .$

But, by the Pythagorean theorem, a² + b² = c², so A + B = C.

Conversely, if we can prove that A + B = C for three similar figures without using the Pythagorean theorem, then we can work backwards to construct a proof of the theorem. For example, the starting center triangle can be replicated and used as a triangle C on its hypotenuse, and two similar right triangles (A and B ) constructed on the other two sides, formed by dividing the central triangle by its altitude. The sum of the areas of the two smaller triangles therefore is that of the third, thus A + B = C and reversing the above logic leads to the Pythagorean theorem a² + b² = c².

Generalization for similar triangles,
green area A + B = blue area C

Pythagoras' theorem using similar right triangles

Generalization for regular pentagons

Law of cosines

The separation s of two points (r₁, θ₁) and (r₂, θ₂) in polar coordinates is given by the law of cosines. Interior angle Δθ = θ₁−θ₂.

Main article: Law of cosines

The Pythagorean theorem is a special case of the more general theorem relating the lengths of sides in any triangle, the law of cosines:^[45]

$a^2+b^2-2ab\cos{\theta}=c^2, \,$

where θ is the angle between sides a and b.

When θ is 90 degrees, then cosθ = 0, and the formula reduces to the usual Pythagorean theorem.

Arbitrary triangle

Main article: Solid geometry

Pythagoras' theorem in three dimensions relates the diagonal AD to the three sides.

A tetrahedron with outward facing right-angle corner

In terms of solid geometry, Pythagoras' theorem can be applied to three dimensions as follows. Consider a rectangular solid as shown in the figure. The length of diagonal BD is found from Pythagoras' theorem as:

$\overline{BD}^{\,2} = \overline{BC}^{\,2} + \overline{CD}^{\,2} \ ,$

where these three sides form a right triangle. Using horizontal diagonal BD and the vertical edge AB, the length of diagonal AD then is found by a second application of Pythagoras' theorem as:

$\overline{AD}^{\,2} = \overline{AB}^{\,2} + \overline{BD}^{\,2} \ ,$

or, doing it all in one step:

$\overline{AD}^{\,2} = \overline{AB}^{\,2} + \overline{BC}^{\,2} + \overline{CD}^{\,2} \ .$

This result is the three-dimensional expression for the magnitude of a vector v (the diagonal AD) in terms of its orthogonal components {v_k} (the three mutually perpendicular sides):

$\|\mathbf{v}\|^2 = \sum_{k=1}^3 \|\mathbf{v}_k\|^2.$

This one-step formulation may be viewed as a generalization of Pythagoras' theorem to higher dimensions. However, this result is really just the repeated application of the original Pythagoras' theorem to a succession of right triangles in a sequence of orthogonal planes.

A substantial generalization of the Pythagorean theorem to three dimensions is de Gua's theorem, named for Jean Paul de Gua de Malves: If a tetrahedron has a right angle corner (like a corner of a cube), then the square of the area of the face opposite the right angle corner is the sum of the squares of the areas of the other three faces. This result can be generalized as in the "n-dimensional Pythagorean theorem":^[51]

Let $x_1, x_2, \ldots,x_n \,$ be orthogonal vectors in ℝⁿ. Consider the n-dimensional simplex S with vertices $0,x_1,\ldots, x_n\,$ . (Think of the (n − 1)-dimensional simplex with vertices $x_1,\ldots,x_n\,$ not including the origin as the "hypotenuse" of S and the remaining (n − 1)-dimensional faces of S as its "legs".) Then the square of the volume of the hypotenuse of S is the sum of the squares of the volumes of the n legs.

This statement is illustrated in three dimensions by the tetrahedron in the figure. The "hypotenuse" is the base of the tetrahedron at the back of the figure, and the "legs" are the three sides emanating from the vertex in the foreground. As the depth of the base from the vertex increases, the area of the "legs" increases, while that of the base is fixed. The theorem suggests that when this depth is at the value creating a right vertex, the generalization of Pythagoras' theorem applies. In a different wording:^[52]

Given an n-rectangular n-dimensional simplex, the square of the (n − 1)-content of the facet opposing the right vertex will equal the sum of the squares of the (n − 1)-contents of the remaining facets.

Inner product spaces

Non-Euclidean geometry

Main article: Non-Euclidean geometry

The Pythagorean theorem is derived from the axioms of Euclidean geometry, and in fact, the Pythagorean theorem given above does not hold in a non-Euclidean geometry.^[58] (The Pythagorean theorem has been shown, in fact, to be equivalent to Euclid's Parallel (Fifth) Postulate.^[59]^[60]) In other words, in non-Euclidean geometry, the relation between the sides of a triangle must necessarily take a non-Pythagorean form. For example, in spherical geometry, all three sides of the right triangle (say a, b, and c) bounding an octant of the unit sphere have length equal to π/2, and all its angles are right angles, which violates the Pythagorean theorem because a² + b² ≠ c².

Here two cases of non-Euclidean geometry are considered—spherical geometry and hyperbolic plane geometry; in each case, as in the Euclidean case for non-right triangles, the result replacing the Pythagorean theorem follows from the appropriate law of cosines.

However, the Pythagorean theorem remains true in hyperbolic geometry and elliptic geometry if the condition that the triangle be right is replaced with the condition that two of the angles sum to the third, say A+B = C. The sides are then related as follows: the sum of the areas of the circles with diameters a and b equals the area of the circle with diameter c.^[61]

Spherical geometry

Main article: Spherical geometry

Spherical triangle

For any right triangle on a sphere of radius R (for example, if γ in the figure is a right angle), with sides a, b, c, the relation between the sides takes the form:^[62]

$\cos \left(\frac{c}{R}\right)=\cos \left(\frac{a}{R}\right)\cos \left(\frac{b}{R}\right).$

This equation can be derived as a special case of the spherical law of cosines that applies to all spherical triangles:

$\cos \left(\frac{c}{R}\right)=\cos \left(\frac{a}{R}\right)\cos \left(\frac{b}{R}\right) +\sin\left(\frac{a}{R}\right) \sin\left(\frac{b}{R}\right) \cos \gamma \ .$

By using the Maclaurin series for the cosine function, cos x ≈ 1 − x²/2, it can be shown that as the radius R approaches infinity and the arguments a/R, b/R and c/R tend to zero, the spherical relation between the sides of a right triangle approaches the form of Pythagoras' theorem. Substituting the approximate quadratic for each of the cosines in the spherical relation for a right triangle:

$1-\left(\frac{c}{R}\right)^2= \left[1-\left(\frac{a}{R}\right)^2 \right]\left[1-\left(\frac{b}{R}\right)^2 \right] + \ \mathrm{higher\ order\ terms}$