|
Instructions
|
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 |
Problem 1
Find the number of subsets
of  that are subsets of neither
that are subsets of neither  nor
nor  .
.
Problem 2
Teams  ,
,  ,
,  , and
, and  are in the playoffs. In the semifinal
matches,
are in the playoffs. In the semifinal
matches,  plays
plays  , and
, and  plays
plays  . The winners of those two matches will play each other in
the final match to determine the champion. When
. The winners of those two matches will play each other in
the final match to determine the champion. When  plays
plays  , the probability that
, the probability that  wins is
wins is  , and the outcomes of all the matches are independent. The
probability that
, and the outcomes of all the matches are independent. The
probability that  will be the champion is
will be the champion is  , where
, where  and
and  are relatively prime positive integers.
Find
are relatively prime positive integers.
Find  .
.
Problem 3
A triangle has
vertices  ,
,  , and
, and  . The probability that a randomly chosen point inside the
triangle is closer to vertex
. The probability that a randomly chosen point inside the
triangle is closer to vertex  than to either vertex
than to either vertex  or vertex
or vertex  can be written as
can be written as  , where
, where  and
and  are relatively prime positive integers.
Find
are relatively prime positive integers.
Find  .
.
Problem 4
Find the number of positive
integers less than or equal to  whose base-three representation contains no
digit equal to
whose base-three representation contains no
digit equal to  .
.
Problem 5
A set contains four numbers.
The six pairwise sums of distinct elements of the set, in no particular order,
are  ,
,  ,
,  ,
,  ,
,  , and
, and  . Find the greatest possible value of
. Find the greatest possible value of  .
.
Problem 6
Find the sum of all positive
integers  such that
such that  is an integer.
is an integer.
Problem 7
Find the number of integer
values of  in the closed interval
in the closed interval ![$[-500,500]$](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_vUuAagg56ulQiwSsP80knu1dJH2LxVz46EDdY7x6Bw3wV6AszLn7En8ddTXkPwOggQCx78b5YSGYXYove_TloYFZzKPiYlQnKHDDTKg4oDI4Yy8XpUVQZ_ShZov0WzmcDUHnoc7SBZA-dX4ldVrqK1vlLA_qoOp2V5Cw=s0-d) for which the equation
for which the equation  has exactly one real solution.
has exactly one real solution.
Problem 8
Find the number of positive
integers  less than
less than  such that
such that![\[1+n+\frac{n^2}{2!}+\frac{n^3}{3!}+\frac{n^4}{4!}+\frac{n^5}{5!}+\frac{n^6}{6!}\]](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_vmIvp4G5DLEp0EFYPT_R-YRRzVGU93b2FSnJfToFhw_qk2krHWEdBepuX4z6NP7lH0xX-aeITBQX8s6br-SmXrxezR3vlW2rzxxTlGL8IUwjniuEL6vQZhHCG4TX_WcBvgXQc6tbXMYaB2mGNzzTO7jp6FLL9ESYNslA=s0-d) is an integer.
is an integer.
Problem 9
A special deck of cards
contains  cards, each labeled with a number
from
cards, each labeled with a number
from  to
to  and colored with one of seven colors. Each
number-color combination appears on exactly one card. Sharon will select a set
of eight cards from the deck at random. Given that she gets at least one card of
each color and at least one card with each number, the probability that Sharon
can discard one of her cards and
and colored with one of seven colors. Each
number-color combination appears on exactly one card. Sharon will select a set
of eight cards from the deck at random. Given that she gets at least one card of
each color and at least one card with each number, the probability that Sharon
can discard one of her cards and  have at least one card of each color and at
least one card with each number is
have at least one card of each color and at
least one card with each number is  , where
, where  and
and  are relatively prime positive integers.
Find
are relatively prime positive integers.
Find  .
.
Problem 10
Rectangle  has side lengths
has side lengths  and
and  . Point
. Point  is the midpoint of
is the midpoint of  , point
, point  is the trisection point of
is the trisection point of  closer to
closer to  , and point
, and point  is the intersection of
is the intersection of  and
and  . Point
. Point  lies on the quadrilateral
lies on the quadrilateral 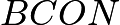 , and
, and  bisects the area of
bisects the area of 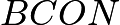 . Find the area of
. Find the area of  .
.
Problem 11
Five towns are connected by a
system of roads. There is exactly one road connecting each pair of towns. Find
the number of ways there are to make all the roads one-way in such a way that it
is still possible to get from any town to any other town using the roads
(possibly passing through other towns on the way).
Problem 12
Circle  has radius
has radius  , and the point
, and the point  is a point on the circle.
Circle
is a point on the circle.
Circle  has radius
has radius  and is internally tangent to
and is internally tangent to  at point
at point  . Point
. Point  lies on circle
lies on circle  so that
so that  is located
is located  counterclockwise from
counterclockwise from  on
on  . Circle
. Circle  has radius
has radius  and is internally tangent to
and is internally tangent to  at point
at point  . In this way a sequence of circles
. In this way a sequence of circles  and a sequence of points on the
circles
and a sequence of points on the
circles  are constructed, where
circle
are constructed, where
circle  has radius
has radius  and is internally tangent to
circle
and is internally tangent to
circle  at point
at point  , and point
, and point  lies on
lies on 
 counterclockwise from point
counterclockwise from point  , as shown in the figure below. There is one
point
, as shown in the figure below. There is one
point  inside all of these circles.
When
inside all of these circles.
When  , the distance from the center
, the distance from the center  to
to  is
is  , where
, where  and
and  are relatively prime positive integers.
Find
are relatively prime positive integers.
Find  .
.
Problem 13
For each
integer  , let
, let  be the number of
be the number of  -element subsets of the vertices of a
regular
-element subsets of the vertices of a
regular  -gon that are the vertices of an isosceles triangle (including
equilateral triangles). Find the sum of all values of
-gon that are the vertices of an isosceles triangle (including
equilateral triangles). Find the sum of all values of  such that
such that  .
.
Problem 14
A  grid of points consists of all points in space
of the form
grid of points consists of all points in space
of the form  , where
, where  ,
,  , and
, and  are integers between
are integers between  and
and  , inclusive. Find the number of different lines that contain
exactly
, inclusive. Find the number of different lines that contain
exactly  of these points.
of these points.
Problem 15
Tetrahedron  has
has  ,
,  , and
, and  . For any point
. For any point  in space, define
in space, define  . The least possible value of
. The least possible value of  can be expressed as
can be expressed as  , where
, where  and
and  are positive integers, and
are positive integers, and  is not divisible by the square of any prime.
Find
is not divisible by the square of any prime.
Find  .
.
AMC 8/10/12
미국수학경시대회
SCAT SSAT PSAT GED SATmath ACT
SCAT SSAT PSAT GED SATmath ACT
국제학교영어원서
강의 수학과학올림피아드
수학과학경시대회 성대
KMC
교육청영재원 교대영재원 경대영재원 준비반 모집
교육청영재원 교대영재원 경대영재원 준비반 모집
상담
환영합니다
053-765-8233 011-549-5206
053-765-8233 011-549-5206
댓글 없음:
댓글 쓰기