녹원학원 수학과학영재교육 010-3549-5206 : 2월 2019

2019년 2월 28일 목요일

삼각수(三角數, triangular number)

삼각수(三角數, triangular number), 또는 "삼각형 수" 는 일정한 물건으로 삼각형 모양을 만들어 늘어 놓았을 때, 그 삼각형을 만들기 위해 사용된 물건의 총 수가 되는 수를 말한다.

예를 들어 아래와 같이 네 줄에 걸쳐 삼각형을 만들었을 때 늘어놓은 물건의 총 수는 10개가 되며, 10은 삼각수의 하나가 된다.

n번째 삼각수 N은 1부터 n까지의 자연수를 모두 합한 것이고, 여기서 삼각수의 정의로 인하여 n은 반드시 자연수여야 한다. 삼각수의 수열은 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78, 91, 105, 120... 과 같고,

n

번째의 삼각수

N

은

N={\frac {n(n+1)}{2}}

으로 나타낼 수 있다. 모든 자연수는 최대 3개의 삼각수의 합으로 표현할 수 있다는 정리가 있으며, 이는 카를 프리드리히 가우스가 1796년 (가우스의 일기에 따르면 7월 10일)에 증명하였다. 이 정리는 모든 자연수는 최대

n

개의

n

각수의 합으로 표현할 수 있다는 페르마의 다각수정리의 한 경우이다.

삼각수의 제곱

$n$ 번째 삼각수의 제곱은 1의 세제곱부터 $n$ 의 세제곱까지의 합과 같다.

사면체수

삼각수의 개념을 공간으로 확장하여, 물체를 사면체를 이루도록 공간에 배치했을 때의 물체의 총 수를 사면체수(四面體數, tertiary number)라고 한다.

제

n

사면체수는 제1 삼각수에서부터 제

n

삼각수까지의 합이고, 그 값

N

은 다시

N={\frac {n(n+1)(n+2)}{6}}

으로 쓸 수 있다.

사면체수를 1항부터 써보면 다음과 같다.

1, 4, 10, 20, 35, 56, 84, 120, 165, 220, 286, 364, 455, 560, 680, 816, 969, 1140, ...

나아가 한번 일반화시키면, 삼각수에서 사면체수를 알아낸 것과 마찬가지로 사면체수의 합으로 4차원 공간에서의 삼각수인 5포체수를 정의할 수 있다. 일반 차원의 공간(여기에서는

r

차원)까지 개념의 확장을 실시했을 때, 제

n

번째의 그 수

T_{r}(n)

은

T_{r}(n)=\prod _{k=1}^{r}\left(1+{\frac {n-1}{k}}\right)={\frac {n(n+1)\cdots (n+r-1)}{r!}}=(-1)^{r-1}{-n \choose r}

이다.

가우스의 계산법]

카를 프리드리히 가우스에 관련된 일화에 의하면, 가우스는 1부터 100까지의 자연수를 모두 더하라는 문제를 듣고(1부터 100까지의 자연수를 모두 더하라는 것은 100번째 삼각수를 구하라는 것과 같다.), 1+100, 2+99 등으로 1~100 사이의 두 수를 더하면 101이 되도록 수를 짝짓고, 합이 101이도록 짝지어진 수들의 갯수가 50쌍이라는 것을 알아낸 뒤 101×50을 계산하여 답이 5050임을 구하였다. 즉, 수식으로 쓰면 (100+1)×(100/2)가 되고, 여기서 100을 n으로 치환하면 n번째 삼각수의 값을 나타내는 식이 도출된다.

위키백과

triangular number 삼각수

A triangular number or triangle number counts objects arranged in an equilateral triangle, as in the diagram on the right. The $n$ th triangular number is the number of dots in the triangular arrangement with $n$ dots on a side, and is equal to the sum of the $n$ natural numbers from 1 to $n$ . The sequence of triangular numbers (sequence A000217 in the OEIS), starting at the 0th triangular number, is

0, 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78, 91, 105, 120, 136, 153, 171, 190, 210, 231, 253, 276, 300, 325, 351, 378, 406, 435, 465, 496, 528, 561, 595, 630, 666...

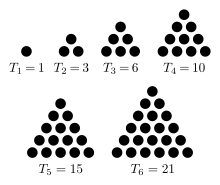
The first six triangular numbers

Formula[edit]

Derivation of triangular numbers from a left-justified Pascal's triangle

The triangle numbers are given by the following explicit formulas:

T_{n}=\sum _{k=1}^{n}k=1+2+3+\dotsb +n={\frac {n(n+1)}{2}}={n+1 \choose 2},

where

\textstyle {n+1 \choose 2}

is a binomial coefficient. It represents the number of distinct pairs that can be selected from

n + 1

objects, and it is read aloud as "

n

plus one choose two".

The first equation can be illustrated using a visual proof.[1] For every triangular number

T_{n}

, imagine a "half-square" arrangement of objects corresponding to the triangular number, as in the figure below. Copying this arrangement and rotating it to create a rectangular figure doubles the number of objects, producing a rectangle with dimensions

n\times (n+1)

, which is also the number of objects in the rectangle. Clearly, the triangular number itself is always exactly half of the number of objects in such a figure, or:

T_{n}={\frac {n(n+1)}{2}}

. The example

T_{4}

follows:

2T_{4}=4(4+1)=20

(green plus yellow) implies that

T_{4}={\frac {4(4+1)}{2}}=10

(green).

Illustration of Triangular Number T 4 Leading to a Rectangle.png

The first equation can also be established using mathematical induction.[2] Since the sum of the first (one) natural number(s) is clearly equal to one, a basis case is established. Assuming the inductive hypothesis for some

n

and adding

n+1

to both sides immediately gives

\sum _{k=1}^{n}k+(n+1)={\frac {n(n+1)}{2}}+(n+1)\rightarrow \sum _{k=1}^{n+1}k={\frac {(n+1)((n+1)+1)}{2}}

In other words, since the proposition

P(n)

(that is, the first equation, or inductive hypothesis itself) is true when

n=1

, and since

P(n)

being true implies that

P(n+1)

is also true, then the first equation is true for all natural numbers. The above argument can be easily modified to start with, and include, zero.

Carl Friedrich Gauss is said to have found this relationship in his early youth, by multiplying

n / 2

pairs of numbers in the sum by the values of each pair

n + 1

.[3] However, regardless of the truth of this story, Gauss was not the first to discover this formula, and some find it likely that its origin goes back to the Pythagoreans 5th century BC.[4] The two formulae were described by the Irish monk Dicuilin about 816 in his Computus.[5]

The triangular number

T n

solves the handshake problem of counting the number of handshakes if each person in a room with

n + 1

people shakes hands once with each person. In other words, the solution to the handshake problem of

n

people is

T n -1

.[6] The function

T

is the additive analog of the factorial function, which is the products of integers from 1 to

n

The number of line segments between closest pairs of dots in the triangle can be represented in terms of the number of dots or with a recurrence relation:

L_{n}=3T_{n-1}=3{n \choose 2};~~~L_{n}=L_{n-1}+3(n-1),~L_{1}=0.

In the limit, the ratio between the two numbers, dots and line segments is

\lim _{n\to \infty }{\frac {T_{n}}{L_{n}}}={\frac {1}{3}}.

Relations to other figurate numbers[edit]

Triangular numbers have a wide variety of relations to other figurate numbers.

Most simply, the sum of two consecutive triangular numbers is a square number, with the sum being the square of the difference between the two (and thus the difference of the two being the square root of the sum). Algebraically,

T_{n}+T_{n-1}=\left({\frac {n^{2}}{2}}+{\frac {n}{2}}\right)+\left({\frac {\left(n-1\right)^{2}}{2}}+{\frac {n-1}{2}}\right)=\left({\frac {n^{2}}{2}}+{\frac {n}{2}}\right)+\left({\frac {n^{2}}{2}}-{\frac {n}{2}}\right)=n^{2}=(T_{n}-T_{n-1})^{2}.

This fact can be demonstrated graphically by positioning the triangles in opposite directions to create a square:

6 + 10 = 16

10 + 15 = 25

There are infinitely many triangular numbers that are also square numbers; e.g., 1, 36, 1225. Some of them can be generated by a simple recursive formula:

S_{n+1}=4S_{n}\left(8S_{n}+1\right)

with

S_{1}=1.

All square triangular numbers are found from the recursion

S_{n}=34S_{n-1}-S_{n-2}+2

with

S_{0}=0

and

S_{1}=1.

A square whose side length is a triangular number can be partitioned into squares and half-squares whose areas add to cubes. This shows that the square of the

n

th triangular number is equal to the sum of the first

n

cube numbers.

Also, the square of the

n

th triangular number is the same as the sum of the cubes of the integers 1 to

n

. This can also be expressed as

\sum _{k=1}^{n}k^{3}=\left(\sum _{k=1}^{n}k\right)^{2}.

The sum of the first

n

triangular numbers is the

n

th tetrahedral number:

\sum _{k=1}^{n}T_{k}=\sum _{k=1}^{n}{\frac {k(k+1)}{2}}={\frac {n(n+1)(n+2)}{6}}.

More generally, the difference between the

n

m

-gonal number and the

n

(m + 1)

-gonal number is the

(n - 1)

th triangular number. For example, the sixth heptagonal number (81) minus the sixth hexagonal number (66) equals the fifth triangular number, 15. Every other triangular number is a hexagonal number. Knowing the triangular numbers, one can reckon any centered polygonal number; the

n

th centered

k

-gonal number is obtained by the formula

Ck_{n}=kT_{n-1}+1

where

T

is a triangular number.

The positive difference of two triangular numbers is a trapezoidal number.

Other properties[edit]

Triangular numbers correspond to the first-degree case of Faulhaber's formula.

Alternating triangular numbers (1, 6, 15, 28, ...) are also hexagonal numbers.

Every even perfect number is triangular (as well as hexagonal), given by the formula

M_{p}2^{p-1}={\frac {M_{p}(M_{p}+1)}{2}}=T_{M_{p}}

where

M p

is a Mersenne prime. No odd perfect numbers are known, hence all known perfect numbers are triangular.

For example, the third triangular number is (3 × 2 =) 6, the seventh is (7 × 4 =) 28, the 31st is (31 × 16 =) 496, and the 127th is (127 × 64 =) 8128.

In base 10, the digital root of a nonzero triangular number is always 1, 3, 6, or 9. Hence every triangular number is either divisible by three or has a remainder of 1 when divided by 9:

0 = 9 × 0

1 = 9 × 0 + 1

3 = 9 × 0 + 3

6 = 9 × 0 + 6

10 = 9 × 1 + 1

15 = 9 × 1 + 6

21 = 9 × 2 + 3

28 = 9 × 3 + 1

36 = 9 × 4

45 = 9 × 5

55 = 9 × 6 + 1

66 = 9 × 7 + 3

78 = 9 × 8 + 6

91 = 9 × 10 + 1

…

There is a more specific property to the triangular numbers that aren't divisible by 3, that is, they either have a remainder 1 or 10 when divided by 27. Those that are equal to 10 mod 27, are also equal to 10 mod 81.

The digital root pattern for triangular numbers, repeating every nine terms, as shown above, is "1, 3, 6, 1, 6, 3, 1, 9, 9".

The converse of the statement above is, however, not always true. For example, the digital root of 12, which is not a triangular number, is 3 and divisible by three.

x

is a triangular number, then

ax + b

is also a triangular number, given

a

is an odd square and

b = a - 1 / 8

b

will always be a triangular number, because

8 T n + 1 = (2 n + 1) 2

, which yields all the odd squares are revealed by multiplying a triangular number by 8 and adding 1, and the process for

b

given

a

is an odd square is the inverse of this operation.

The first several pairs of this form (not counting

1 x + 0

) are:

9 x + 1

25 x + 3

49 x + 6

81 x + 10

121 x + 15

169 x + 21

, … etc. Given

x

is equal to

T n

, these formulas yield

T 3 n + 1

T 5 n + 2

T 7 n + 3

T 9 n + 4

, and so on.

The sum of the reciprocals of all the nonzero triangular numbers is

\!\ \sum _{n=1}^{\infty }{1 \over {{n^{2}+n} \over 2}}=2\sum _{n=1}^{\infty }{1 \over {n^{2}+n}}=2.

This can be shown by using the basic sum of a telescoping series:

\!\ \sum _{n=1}^{\infty }{1 \over {n(n+1)}}=1.

Two other interesting formulas regarding triangular numbers are

T_{a+b}=T_{a}+T_{b}+ab

and

T_{ab}=T_{a}T_{b}+T_{a-1}T_{b-1},

both of which can easily be established either by looking at dot patterns (see above) or with some simple algebra.

In 1796, German mathematician and scientist Carl Friedrich Gauss discovered that every positive integer is representable as a sum of three triangular numbers (possibly including

T 0

= 0), writing in his diary his famous words, "ΕΥΡΗΚΑ! num = Δ + Δ + Δ". Note that this theorem does not imply that the triangular numbers are different (as in the case of 20 = 10 + 10 + 0), nor that a solution with exactly three nonzero triangular numbers must exist. This is a special case of the Fermat polygonal number theorem.

The largest triangular number of the form

2 k - 1

is 4095 (see Ramanujan–Nagell equation).

Wacław Franciszek Sierpiński posed the question as to the existence of four distinct triangular numbers in geometric progression. It was conjectured by Polish mathematician Kazimierz Szymiczek to be impossible and was later proven by Fang and Chen in 2007.[7][8]

Formulas involving expressing an integer as the sum of triangular numbers are connected to theta functions, in particular the Ramanujan theta function.[9][10]

Applications[edit]

A fully connected network of

n

computing devices requires the presence of

T n - 1

cables or other connections; this is equivalent to the handshake problem mentioned above.

In a tournament format that uses a round-robin group stage, the number of matches that need to be played between

n

teams is equal to the triangular number

T n - 1

. For example, a group stage with 4 teams requires 6 matches, and a group stage with 8 teams requires 28 matches. This is also equivalent to the handshake problem and fully connected network problems.

One way of calculating the depreciation of an asset is the sum-of-years' digits method, which involves finding

T n

, where

n

is the length in years of the asset's useful life. Each year, the item loses

(b - s) \times n - y / T n

, where

b

is the item's beginning value (in units of currency),

s

is its final salvage value,

n

is the total number of years the item is usable, and

y

the current year in the depreciation schedule. Under this method, an item with a usable life of

n

= 4 years would lose 4/10 of its "losable" value in the first year, 3/10 in the second, 2/10 in the third, and 1/10 in the fourth, accumulating a total depreciation of 10/10 (the whole) of the losable value.

Triangular roots and tests for triangular numbers[edit]

By analogy with the square root of

x

, one can define the (positive) triangular root of

x

as the number

n

such that

T n = x

:[11]

n={\frac {{\sqrt {8x+1}}-1}{2}}

which follows immediately from the quadratic formula. So an integer

x

is triangular if and only if

8 x + 1

is a square. Equivalently, if the positive triangular root

n

x

is an integer, then

x

is the

n

th triangular number.[11]

Wikipedia