고대 그리스 수학자 에우클레이데스(영어로 유클리드)가 저서 '원론'에서 소개한 수학체계인 ‘유클리드 기하학’은 2000년 동안 서구 문명을 지배했다. 그러나 19세기 초 굳게 믿었던 유클리드 기하학 체계의 토대 중 하나를 의심하자 ‘비유클리드 기하학’이 등장했다. 인문학과 수학의 시선에서 두 기하학을 살펴본다.
Q(수학자). 초중고에서 배우는 기하인 유클리드 기하학의 정수라고 할 수 있는 '원론'은 어떤 책인가요.
A(인문학자). "'안녕원론'은 기원전 3세기에 고대 그리스 (수학자) 에우클레이데스가 그 당시까지 알려져 있던 수학적 지식을 집대성한 기하학 책이에요. 평면기하 입체기하 수론 등 다양한 내용을 총 13권에 담았어요.
이 작품의 그리스어 원제목은 ‘Στοιχεῖα(스토이케이아)’입니다. 이를 그대로 번역하면 요소들이라는 뜻이에요. 다시 말하자면 기하학을 계속 쌓아 나가기 위한 주춧돌 즉 지식의 핵심 요소를 모았다는 것이지요.
에우클레이데스가 많은 명제를 한데 모으려고 했던 배경에는 그가 살았던 알렉산드리아의 도서관에서 실마리를 찾을 수 있습니다. 수많은 학자가 알렉산드리아 대도서관에서 의학 지리학 문학 등 각 분야의 지식을 수집해서 목록화하는 작업을 했지요. 에우클레이데스가 '원론'을 쓴 의도가 담긴 서문은 남아있진 않지만 기하학도 당시 지식의 체계화 작업의 일환으로 볼 수 있어요."
Q (수학자). '원론'이 역사적으로 중요한 책으로 평가받게 된 이유는 뭔가요.
A(인문학자). "두 가지 면에서 '원론'의 중요성을 이야기할 수 있어요. 첫째는 기하학 자체가 중요하기 때문이에요. 고대 그리스 철학자 플라톤의 대화편들에 남아있듯이 고대 그리스에서 기하학은 궁극의 지적 훈련인 철학을 하기 위해 논리적으로 사유하고 성찰하기 위한 가장 필수적 훈련으로 여겨져 왔어요. '원론'은 그런 훈련을 하기 위한 ‘교과서’ 역할을 했다고 볼 수 있습니다.
둘째는 '원론'의 탁월한 구성 체계 때문인데요. '원론'은 연역적 체계로 이뤄진 책입니다. 정의와 공준에서 시작해서 이전 것에서부터 다음 것을 증명해 나가면서 총 465개의 명제를 연역적으로 꿰어낸 논리적 아름다움이 있어요."
Q(수학자). 에우클레이데스가 활동했을 때로부터 무려 2000년이 넘도록 서구 문명에서는 계속해서 '원론'을 공부했나요.
A(인문학자). " 네 맞아요. 에우클레이데스가 기원전 3세기쯤 '원론'을 펴낸 이후 서구 전역에 전승됩니다. 이집트에서 발굴된 기원후 1세기경 파피루스에도 학생들이 '원론'을 공부한 기록이 남아있어요. 9세기에는 이슬람의 학자들에 의해서 아랍어로 번역되었다가 12세기 스페인 톨레도에서 라틴어로 번역됩니다. 1482년 최초의 '원론' 인쇄본이 나온 뒤 이 책이 급격히 퍼지기 시작하면서 16세기에는 여러 개정판과 영어 이탈리아어 등의 번역본도 나오지요.
유럽에서 오래된 대학 중 하나인 프랑스 파리대나 영국 옥스포드대의 학생은 졸업을 위해서 '원론'을 반드시 공부했어야 할 만큼 서구에서는 '원론'의 중요성을 일찍부터 강조했습니다."
Q(인문학자). '원론'에서 시작한 유클리드 기하학의 지위가 영원히 견고할 것 같았는데 19세기 초 균열이 일어나요. 유클리드 기하학의 토대를 이루는 5개의 공준 중 ‘평행선 공준’ 때문인데요 어떤 내용인가요.
A(수학자). "먼저 공준이 무엇인지부터 이야기해볼게요. 바둑을 둘 때 기본적인 규칙이 존재하지요. 바둑판의 격자점 위에 검은 돌과 흰 돌을 하나씩 번갈아 가며 올려야 해요.
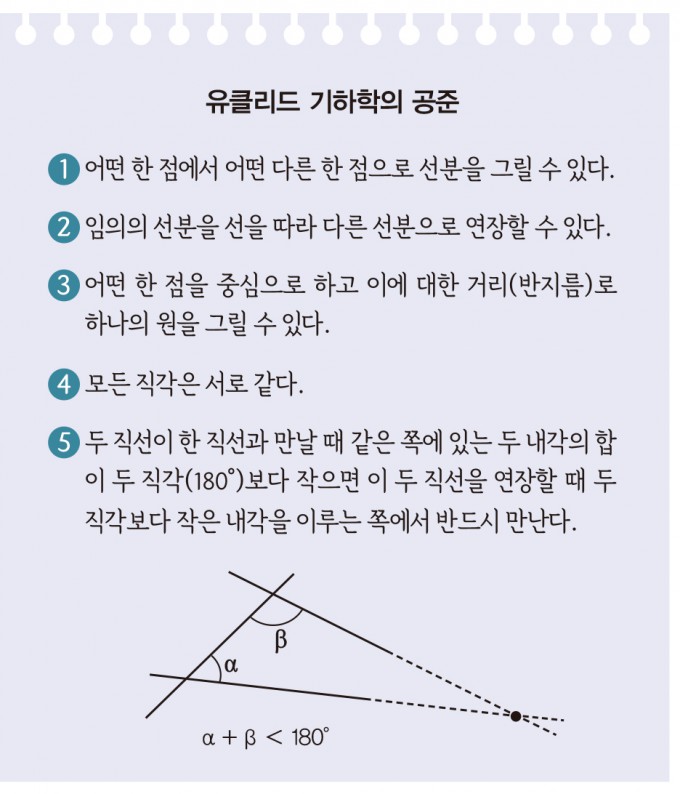
수학에서도 문제를 풀기 위한 규칙을 먼저 정해요 이 규칙을 ‘공준’이라고 부르고 공준이 정해지면 그 안에서 자유롭게 문제를 풀 수 있지요. '원론'을 보면 기하학에서 지켜야 하는 공준이 5개 있어요.
5번째 공준을 다르게 표현하면 ‘임의의 직선이 있고 그 직선 밖에 점이 있을 때 이 점을 지나며 원래의 직선과 평행한 직선은 단 하나만 존재한다’는 거예요. 이를 흔히 평행선 공준이라고 부르지요."
Q(인문학자). 평행선 공준이 왜 문제가 됐던 건가요.
A(수학자). "수학자들은 증명을 하지 않아도 되는 약속인 공준을 최소한으로 사용해 유클리드 기하학 체계를 구축하고 싶었어요. 그래서 나머지 4개의 공준을 이용해 평행선 공준을 증명하려고 노력했어요. 그러나 에우클레이데스가 처음 이 공준을 소개하고 2000년이 지나도록 평행선 공준 은 증명되지 않았어요.
19세기 수학자들은 평행선 공준을 그대로 증명하기 어렵다고 판단하고 명제를 거짓이라고 가정할 때 생기는 모순을 보여 역으로 명제를 증명하는 ‘귀류법’을 활용하기로 했습니다. 그런데 평행선 공준을 거짓이라고 생각해도 전혀 기하학에 모순이 생기지 않았어요. 당시 수학자들은 평행선 공준을 거짓으로 하는 새로운 기하학이 있지 않을까 생각하게 됐고 이것이 바로 ‘비유클리드 기하학’입니다."
Q(인문학자). 그렇게 나온 비유클리드 기하학이 어떻게 기하학을 발전시켰나요.
A(수학자). "간단한 예시를 들어 유클리드 기하학과 비유클리드 기하학을 비교해볼게요. ‘삼각형의 내각의 합은 180’라는 명제가 있어요 우리는 이 명제를 참으로 받아들이고 있는데요. 이를 증명할 때 가장 먼저 삼각형의 한 변을 기준으로 맞은 편 꼭짓점을 지나는 평행선을 그어요. 즉 삼각형의 내각의 합이 180가 되기 위해서는 평행선 공준이 필요합니다. 만약 내각의 합이 180가 아니라면 평행선 공준도 거짓이 되지요.
그런데 우리가 사는 지구를 떠올려 보세요. 지구는 구면이잖아요. 지구 위 북극에서 한 점을 잡고 구면을 따라 90의 각도로 선을 2개 내리고 적도 위에 선을 그어 삼각형을 만들면 이 삼각형의 내각의 합은 180가 아니라 270가 됩니다. 이런 기하학 체계를 ‘구면기하학’ 혹은 ‘타원기하학’이라고 하는데요. 평행선 공준의 표현을 빌리자면 타원 위에서 선 밖의 한 점을 지나 그 직선에 평행한 직선은 존재하지 않습니다.
반대로 선 밖의 한 점을 지나 그 직선에 평행한 직선이 무한히 많이 존재하는 기하학도 있어요. 이를 ‘쌍곡기하학’이라고 하는데요. 말 안장 혹은 감자칩 모양의 공간을 떠올리면 됩니다 이 공간 위에서 삼각형을 그리면 이 삼각형의 내각의 합은 180보다 작지요.
초중고생 때는 유클리드 기하학을 기본에 둔 기하학을 배우기 때문에 유클리드 기하학의 원리가 자명해보일 거예요. 하지만 실제 우리가 사는 세상은 곡면이기 때문에 어떻게 보면 유클리드 기하학이 아니라 비유클리드 기하학이 세상을 더 잘 설명해요. 그러므로 평행선 공준을 증명하기 위해 발상을 전환한 일이 우리의 세계를 더 잘 표현하게 된 놀라운 결과를 이끌어 냈지요."
Q(인문학자). 지금까지 유클리드 기하학이 왜 중요하게 여겨졌는지 그럼에도 불구하고 유클리드 기하학이 아닌 기하학이 어떻게 생겨났는지를 이야기해 왔는데요. 유클리드 기하학이 서구 문명을 지배한 것은 에우클레이데스 덕분만은 아니에요.
2000년간 '원론'에 여러 사람의 생각을 보태서 더 멋진 유클리드 기하학 체계를 만들어 왔습니다. '원론'을 중요하게 여겼던 여러 서구의 지식인이 유클리드 기하학을 더 견고하게 만들었다고 평가할 수 있지요.
다만 19세기 초 비유클리드 기하학의 등장은 학문에서 가져야 할 시사점을 주는 것 같습니다. 왜냐하면 '원론'은 기하학의 훌륭한 교과서 역할을 했지만 어떤 의미에선 마치 전제 군주처럼 2000년 동안 기하학적 공간에 대한 사고를 얽매고 있었다고 할 수 있으니까요.
그래서 비록 우리가 유클리드 기하학이 왜 서구 문명을 지배해왔느냐로 이야기를 시작했지만 그토록 오래 지배했던 기하학이 어떻게 무너졌느냐가 더 생각할 지점이 많지요.
A(수학자). "교수님 말씀처럼 비유클리드 기하학의 등장은 기존 기하학 체계를 무너뜨렸다고 볼 수 있지만 어떻게 보면 기하학의 범위를 넓혔다고도 볼 수 있는데요. 비유클리드 기하학은 수학이라는 학문적 관점에서도 큰 의미를 갖고 있어요.
평행선 공준처럼 너무나도 당연하게 여겼던 공준을 바꿔도 전혀 모순이 발생하지 않는 새로운 기하학을 세울 수 있다는 걸 알게 되면서 일부 수학자는 공준을 쌓아 올려 모든 명제를 증명할 수 있는 완전무결한 수학체계를 만들고자 했어요. 독일 수학자 고틀로프 프레게(1848~1925), 다비트 힐베르트(1862~1943), 영국 수학자 버트런드 러셀(1872~1970)이 대표적이지요.
끝내 미국 수학자 쿠르트 괴델(1906~1978)에 의해 그 시도는 불가능하다고 판별이 났어요. 모순 없는 체계에는 증명하지 못하는 명제가 있다는 거지요. 이는 수학이 계속해서 새롭게 진화할 수 있다는 걸 의미해요. 그렇게 보면 유클리드 기하학에서 비유클리드 기하학으로 넘어가는 과정은 인류 지성사의 발전을 볼 수 있었던 한 단면이 아닐까 하고 생각합니다."
Q(인문학자). 비유클리드 기하학으로 수학이 어떻게 지적인 도약을 했는가를 잘 요약해주신 것 같아요. 그런데 비유클리드 기하학은 수학의 발전뿐 아니라 과학의 발전에도 엄청나게 기여했잖아요. 그 부분도 짚어주세요.
A(수학자). "수학의 발전은 과학 특히 물리와 떼려야 뗄 수 없는데요. 뉴턴의 고전 역학은 유클리드 기하학에 기반해 이뤄져 있어요. 하지만 현대 물리학의 핵심인 알베르트 아인슈타인의 상대성 이론을 설명하기 위해서는 비유클리드 기하학이 필요해요.
대표적인 예로 길을 찾을 때 쓰는 GPS가 있어요. GPS는 지구 밖에 있는 인공위성에서 신호를 주고받아서 위치를 추적해요. 이 인공위성의 시간을 보정하기 위해서는 상대성 이론이 필요하고 그게 비유클리드 기하학을 통해서 계산이 이뤄지지요. 이런 식으로 수학의 발전이 물리학의 발전을 이루고 결국 기술의 발전까지 이뤄져서 현대 사회를 이루는 근간이 된다고도 생각할 수 있습니다."
수학동아 6월



댓글 없음:
댓글 쓰기