Circles O and Q are tangent externally at T (see the figure below).
If AB and CD are common external tangents,
prove that ABCD is a bicentric trapezoid with incenter T and circumcenter O1.
If AB and CD are common external tangents,
prove that ABCD is a bicentric trapezoid with incenter T and circumcenter O1.
Circles O and Q are tangent externally at T (see the figure below).
If AB and CD are common external tangents,
prove that ABCD is a bicentric trapezoid with incenter T and circumcenter O1.
Extend AB, DC to meet at E. Then EBA and ECD are tangents drawn to the 2 circles from an external point E and are hence equal for each circle.
So Tr.s EAD & EBC are isoceles and similar since they share the same angle <E. So BC//AD and < B = < D. Hence ABCD is a cyclic trapezoid with AB = CD.
The circumcentre of ABCD must lie on OQ the perpendicular bisector of both AD and BC. Find O1 on OQ such that AO1 = BO1 and we can see easily thro congruence that these are also equal to DO1 and CO1. Hence O1 is the circumcentre
Now draw the common internal tangent at T which is seen to bisect AB and CD so AT is perpendicular to BT and likewise DT to CT. Hence thro congruence we can show that the perpendiculars from T to ths 4 sides are all equal hence ABCD has an incircle with T as centre
Since EA = ET = EB, FC = FT = FD and AB = CD.
Also AD//BC so ABCD is an isosceles trapezoid.
Then EF = (AD + BC)/2. (see the solution of problem 1008).
EF = AB = CD so AB + CD = AD + BC then ABCD is circumscribed quadrilateral .
Any isosceles trapezoid is a cyclic quadrilateral.
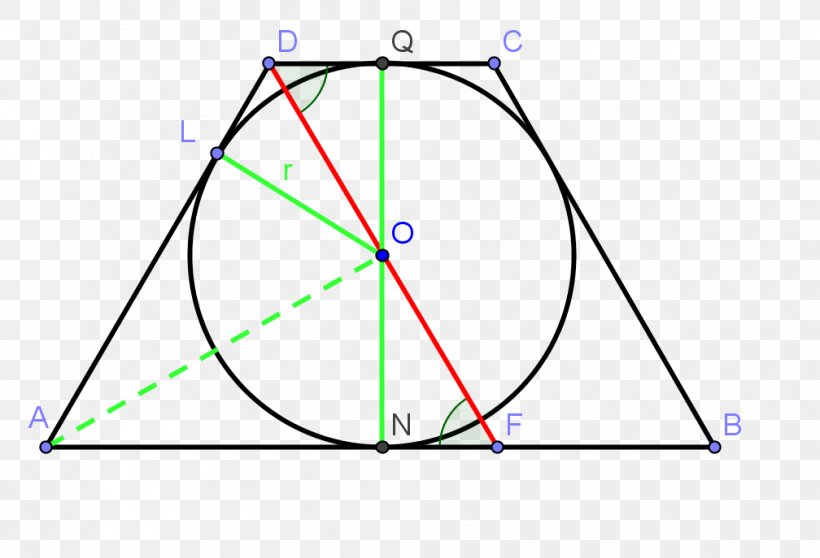
If AB and CD are common external tangents,
prove that ABCD is a bicentric trapezoid with incenter T and circumcenter O1.
Extend AB, DC to meet at E. Then EBA and ECD are tangents drawn to the 2 circles from an external point E and are hence equal for each circle.
So Tr.s EAD & EBC are isoceles and similar since they share the same angle <E. So BC//AD and < B = < D. Hence ABCD is a cyclic trapezoid with AB = CD.
The circumcentre of ABCD must lie on OQ the perpendicular bisector of both AD and BC. Find O1 on OQ such that AO1 = BO1 and we can see easily thro congruence that these are also equal to DO1 and CO1. Hence O1 is the circumcentre
Now draw the common internal tangent at T which is seen to bisect AB and CD so AT is perpendicular to BT and likewise DT to CT. Hence thro congruence we can show that the perpendiculars from T to ths 4 sides are all equal hence ABCD has an incircle with T as centre
Since EA = ET = EB, FC = FT = FD and AB = CD.
Also AD//BC so ABCD is an isosceles trapezoid.
Then EF = (AD + BC)/2. (see the solution of problem 1008).
EF = AB = CD so AB + CD = AD + BC then ABCD is circumscribed quadrilateral .
Any isosceles trapezoid is a cyclic quadrilateral.
Angle - Angle Isosceles Trapezoid Beírt Kör Circle

댓글 없음:
댓글 쓰기