
빅 보이는 1940년대에서 1950년대 사이에 미국에서 사용되었던 증기 기관차이다. 그 무게만 무려 567톤에 달하는데, 3600톤의 화물을 싣고도 100km/h의 속력으로 달릴 수 있는 엄청난 힘을 자랑했다. 이 증기 기관차를 움직이는 힘은 어디에서 기인할까?
학습 목표
- 이상 기체 상태 방정식으로 이상 기체의 특성을 설명할 수 있다.
- 기체의 내부 에너지와 온도, 압력 등을 분자 운동 모형으로 설명할 수 있다.
- 등분배 정리를 이용하여 내부 에너지를 계산할 수 있다.
- 열과 일의 출입과 관련한 열역학 제1법칙을 이해하고 다양한 열역학 과정을 설명할 수 있다.
물리학 전개도

증기 기관은 석탄 등의 연료를 태워 여기서 발생하는 열을 이용해 물을 고온 고압의 수증기로 변화시킨다. 이 수증기가 팽창하여 피스톤을 밀어내고 피스톤이 움직이는 힘과 에너지로 증기 기관이 작동하는 것이다.
이와 같이 열과 온도와 관련된 현상을 다루는 열역학에 대해 공부할 것이며 이상 기체 계를 상정하여 열과 에너지의 관계를 다루는 열역학 제1법칙과 온도와 열 출입에 의해 결정되는 엔트로피와 관련된 열역학 제2법칙을 이해해보자.
1. 이상 기체 상태 방정식
기체의 상태는 부피, 압력, 온도에 의해 특정된다. 이때 기체 분자들끼리 어떠한 상호 작용을 하지 않는 가상의 기체를 '이상 기체'라 하고 이상 기체의 상태, '부피-압력-온도' 는 다음과 같은 관계를 만족한다.


위의 식을 '이상기체의 상태 방정식'이라 한다. 이를 통해서 온도가 일정한 상태에서 부피와 압력의 반비례 관계(=보일의 법칙), 압력이 일정할 때 온도와 부피의 비례 관계(=샤를의 법칙)를 확인할 수 있다.
실온과 대기압 하에서 공기 분자들의 평균 거리는 대략 분자 크기의 열 배쯤 된다. 기체 분자 간의 거리가 충분히 멀면 분자들끼리 상호작용 하는 효과가 미미하기 때문에 일상의 공기를 이상 기체로 간주할 수 있다.
2. 기체 운동론
온도, 압력, 부피는 기체 분자들의 디테일한 움직임을 평균값으로 치환하여 표현한 거시적인 물리량이다.
개별 분자들의 디테일한 운동이 에너지, 온도, 압력에 어떻게 영향을 미치는지 간단한 모형을 이용하여 살펴보자.


케틀레의 통계 이론에 영감을 받은 맥스웰; 낯선 것에서 낯익은 것을 창조하는 융합적 구조 접속
오래전부터 사람들은 공기, 즉 기체가 어떻게 움직이는지 상상해왔다. 그러나 기체에는 너무나 많은 기체 알갱이들이 포함되어 있을 것이기 때문에, 기체 알갱이 몇 개의 운동을 안다고 해도 그 기체들이 어마어마하게 모였을 때 나타나는 효과를 계산하기는 어려웠다. 그렇다면 어떻게 해야 수많은 기체 알갱이들의 운동을 계산할 수 있을까?


맥스웰은 벨기에의 통계학자이자 천문학자인 케틀레가 발전시킨 통계적 방법에서 아이디어를 얻었다. 케틀레는 수많은 인간들의 집단이라 볼 수 있는 사회에서 나타나는 여러 현상들이 매우 복잡해 보이지만, 그 안에 규칙성이 있을 것이라고 생각했다. 그 결과는 정상분포 곡선을 그릴 것이며 그것을 통해 곡선의 평균값에 해당하는 '평균적 인간'의 특성을 포착해낼 수 있을 것이라고 생각했다.

맥스웰은 기체 입자 각각은 0에 가까운 아주 느린 속도부터 엄청 빠른 속도까지 매우 다양한 속도를 갖겠지만 기체 입자들의 속도 전체를 모아놓고 보면 정상분포 곡선을 그릴 것이라는 가정하에 기체 입자들의 속도 분포 곡선으로부터 그 기체의 물리적 특성을 찾아내는 방법을 개척해나갔다. 이를 통해 기체 입자의 운동을 다루는 통계적이고 확률적인 방법을 세운 것이다.
맥스웰이 기체를 다루는 창조적인 방법을 찾아낸 것은 인간과 사회를 대상으로 한 분석을 통해서였다. 케틀레의 통계적 분석 방법 자체는 이미 천문학에서 사용되고 있었던 것이지만 그것으로 집단의 특성을 분석한다는 구상은 케틀레를 통해 얻었다. 한마디로 '맥스웰의 분자'는 '케틀레의 사회'에서 영감을 얻은 것이다. 맥스웰은 정상분포곡선 개념을 차용하여 기체 입자의 운동을 다루는 통계적이고 확률적인 방법을 세운 것이다.
3. 내부 에너지
내부 에너지는 계를 이루는 분자들이 가질 수 있는 총 에너지를 의미한다. 따라서 기체 분자의 운동 에너지 이외에도 기체 분자 간의 화학 결합 에너지나 입자들의 질량에 의한 정지 에너지 등도 따져봐야 한다. 하지만 이상 기체의 내부 에너지는 오로지 기체 분자의 운동 에너지만을 의미한다.
등분배 정리
앞서 구했듯이 단원자 분자 이상 기체의 병진 운동에너지는 K=3/2NkT이다. 이는 계의 내부 에너지 U가 3/2 NkT라는 뜻이다. 이처럼 이상 기체의 내부 에너지는 온도에만 의존하는 함수이다. 한편 한 방향의 병진 운동에 대한 분자당 평균 운동 에너지는 1/2kT이고, 입자는 세 방향(x, y, z)으로 움직이므로 각 방향당 1/2kT만큼의 에너지가 균등하게 분배된다고 볼 수 있다. 이를 '등분배 정리'라고 한다. 운동 에너지처럼 2차 함수 형태로 표현되는 에너지는 회전 운동 에너지, 탄성에 의한 진동 에너지가 있는데 이들도 각각 1/2kT만큼의 에너지 값을 갖는다. 만약 N개의 분자들로 이루어진 계에서 분자들이 2차 함수 형태로 표현되는 f개의 에너지를 갖고 있다면 이 계의 내부 에너지는 등분배 정리에 의해 U= f/2NkT가 된다.
| 운동 상황 | f(자유도) |
| 3차원 병진 운동만 하는 경우 | 3 |
| 3차원 병진 운동 + 회전 | 3+1 |
| 3차원 병진 운동 + 탄성 진동 | 3+1 |
| 3차원 병진 운동 + 회전 + 탄성 진동 | 3+1+1 |
4. 열과 일
물체에 열 Q를 가하면 물체의 온도가 △T 만큼 변화하게 된다. 이것을 정량적으로 표현하면
Q = C △T (= △U + W)
한 물체의 온도를 △T 만큼 변화시키는 데 필요한 열의 양을 Q라 하면 물체에 따라 필요한 열의 양이 다를 것이므로 물체의 특성을 반영한 물리량이 필요하다. 이것을 물체의 열용량 C라 하고, 열용량 C은 물체의 온도 1도 올리는 데 필요한 열의 양으로 정의한다.
열의 일당량

줄은 그림과 같이 회전할 수 있는 날개가 있는 용기에 물을 담고 외부에서 일을 하여 날개를 회전시키는 실험을 하였다. 그 결과 물의 온도가 올라가는 것을 확인하였고 날개를 돌리는 데 해준 일과 물의 온도 증가로부터 열과 일 사이에 정량적으로 1cal = 4.18J의 관계가 성립한다는 것을 알아냈다. 줄은 계에 에너지를 전달한다는 면에서 일(W)과 열(Q)이 동등하다는 사실을 알아냈고, 그 관계를 '열의 일당량'이라 했다.
열역학 제0법칙
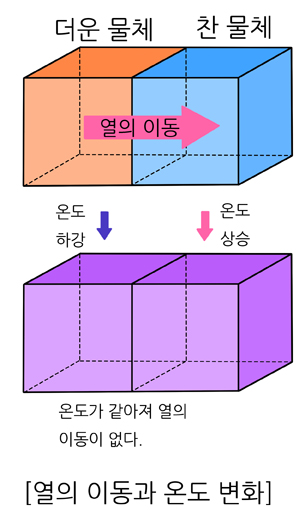
열은 계에 에너지를 전달하는 한 방식으로, 온도가 다른 두 물체를 접촉시키면 자발적으로 온도가 높은 곳에서 낮은 곳으로 전달되는 에너지이며, 두 계의 온도가 같아질 때까지 열 에너지는 이동한다. 이때 두 계는 열평형 상태에 도달한다고 정의한다.
5. 열역학 제 1법칙
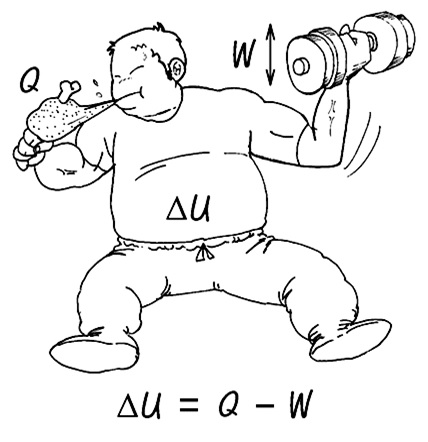
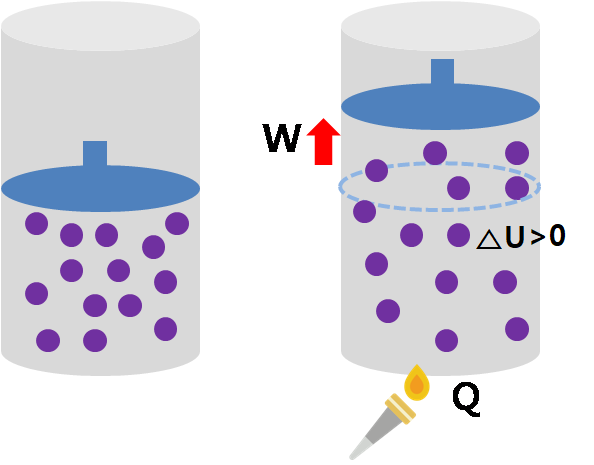
밥을 먹고(Q) 몸을 움직이면(W) 그 차이만큼의 에너지(△U)가 남는다. 그때 세 변수의 관계는 다음과 같다.
△U = Q - W
이제 오른쪽 그림을 보자. 어떤 계의 내부 에너지 변화량(△U)은 외부에서 계에 공급된 열(Q)에서 계가 외부에 한 일(W)을 뺀 양과 일치함을 알 수 있다. 이 관계를 설명하는 법칙이 '열역학 제1법칙'이다.
열역학 제1법칙: Q=△U+W
사실 열역학 제1법칙은 열 에너지와 역학적 에너지를 포함한 보다 일반화된 '에너지 보존 법칙'이다.
부호 규칙
| Q>0 계가 열을 흡수 | Q<0 계의 열이 방출 |
| △U>0 계의 온도 증가 | △U<0 계의 온도 감소 |
| W>0 기체가 외부에 일을 함 | W<0 기체가 외부로부터 일을 받음 |
6. 열역학 과정
기체가 팽창을 하는 경우, 기체가 하는 일은 힘과 이동 거리로 나타내기보다 압력과 부피로 나타내는 것이 편리하다. 기체가 처음 부피에서 나중 부피로 변할 때 기체가 한 일 W는

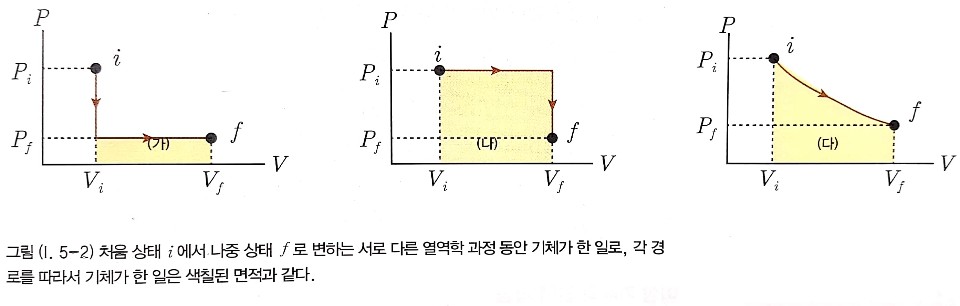
그림을 보면 처음 상태와 나중 상태가 같더라도 다른 열역학 과정을 따르는 경우 기체가 한 일은 달라진다.
1) 등압 과정
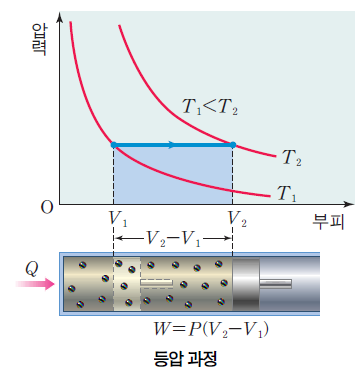
등압 과정시 압력 P가 변하지 않는다. 열역학 제1법칙 Q = △U + W(P△V) 에 의해서 열 출입이 내부 에너지와 부피의 변화에 기여하는 과정이다.

반대의 과정에서는 (압력이 일정하지만 부피가 줄어드는 경우) △V<0 이므로 W<0 이고, 온도가 감소하므로 △U<0이어서 Q<0 이게 된다. 이 경우는 계가 열을 방출한다.
2) 정적 과정
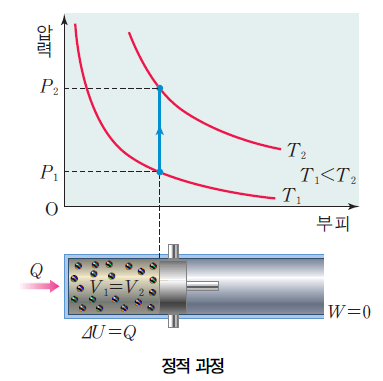
정적 과정시 부피 V가 변하지 않는다. 열역학 제1법칙 Q = △U + W(P△V) , 즉 W=0이 된다.
이 과정에서는 열 출입이 내부 에너지 변화에만 기여한다.

반대의 과정엔 온도가 감소하므로 계가 방출한 열만큼 내부 에너지가 감소한다.
3) 등온 과정
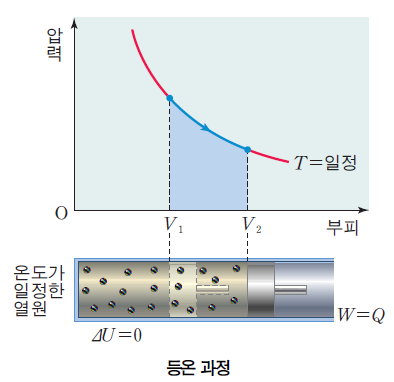
등온 과정시 온도 T가 일정하다. 열역학 제1법칙 Q = △U + W(P△V) 에 의해서 △U=0이 됨을 알 수 있다.
따라서 열 출입이 기체의 일에만 기여한다. 이때 일의 양을 구해보자. 이때는 압력이 부피에 따라 변하므로


4) 단열 과정
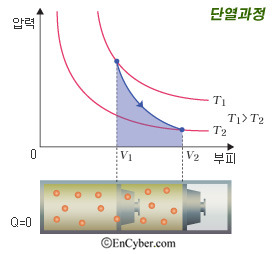
단열 과정은 외부로의 열출입이 없는 열역학 과정이다 따라서 Q=0이다. 열역학 제1법칙 Q = △U + W(P△V) 에 의해서 △U = - W 이다. 즉 기체가 외부에 일을 하면 (부피가 팽창하면) 계의 온도는 낮아지고, 기체가 외부로부터 일을 받으면 (부피가 수축하면) 계의 온도는 높아진다.

그림을 보면 단열선은 등온선보다 훨씬 가파르다. 등온선에 한해서는 PV=NkT(T가 상수)에 의해 PV=상수, 즉 부피와 압력이 반비례한다. 단열선도 얼핏 볼 때, 부피와 압력이 반비례하는 것처럼 보이지만, 부피와 압력의 정량적인 관계는 다음과 같이 정의된다.

단원자 이상 기체의 등적 몰비열, 등압 몰비열을 구해보고 단열선에 적용되는 부피, 압력 관계를 증명하겠다.
이는 카르노 기관에서 열효율을 구하기 위해 알아야 할 선행 개념이므로 꼭 이해하자.
몰비열비

단열선에서 부피와 압력의 관계

댓글 없음:
댓글 쓰기