학습 목표
통계적인 관점에서의 엔트로피를 이해하고, 열역학 제2법칙을 설명할 수 있다.
1. 열역학 제2법칙
엔트로피의 정성적 접근
시간은 변화에 대한 관념이자 변화를 기술하기 위한 가상적 개념에 지나지 않는다. 자연에서 시간의 방향을 정해주는 것이 '엔트로피'이다. 시간은 변화에 있어서 '무질서'를 지향한다. 이처럼 자연의 모든 것은 무질서로 귀결된다는 법칙이 '열역학 제2법칙'이다. '열역학 제2법칙'이 성립하지 않는 것은 운동량이나 에너지 보존 법칙이 성립하지 않는 것보다 더 이상한 일이다.
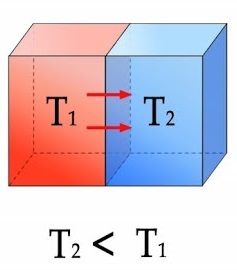
뜨거운 물체가 식어가는 건 열이 고온에서 저온으로 이동하기 때문이며 너무나 자연스러운 반응이다. 그러나 열이 저온에서 고온으로 이동하여 뜨거운 물체가 더 뜨거워지는 것은 너무나 부자연스럽다. 이처럼 엔트로피는 열의 이동 방향을 고온에서 저온으로 결정한다.
2. 열기관
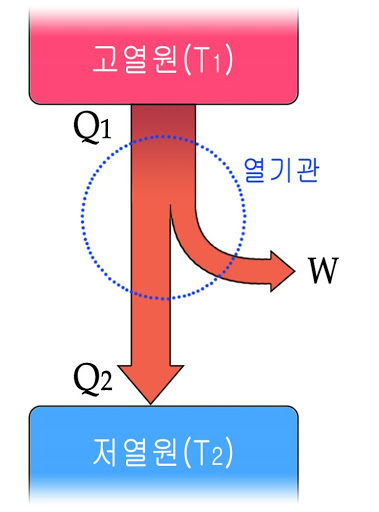
열은 고온에서 저온으로 이동하는 에너지다. 열기관은 이 흐름을 이용해서 열의 일부를 일로 전환한다. 이때 열기관의 열효율은 다음과 같다.
1) 열효율
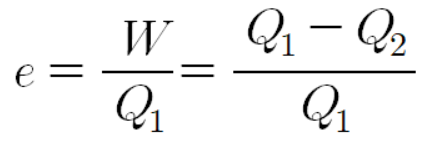
열기관이 한 번의 순환 과정 동안 한 일 W가 Q1-Q2로 정의되는 이유는 다음과 같다.
열기관은 한 번의 순환 과정을 거치면 다시 원래의 상태로 되돌아오므로, 한 번의 순환 과정 동안 열기관의 내부 에너지는 변화가 없다.

열효율 100%와 엔트로피
열효율이 100%인 열기관을 만들 수 있을까? 이론상은 가능하다. 열 Q2를 0으로 만들면 된다. 버려지는 열(Q2)을 0으로 만들어서 투입한 열을 모두 일로 전환하겠다는 건 에너지 보존 법칙에도 위배되지 않는다. 그러나 열기관이 지속적으로 일하기 위해선 순환 과정을 거쳐야 한다. 이를 위해선 버려지는 열이 꼭 있어야 함을 의미한다. P-V그래프를 통해 이를 확인할 수 있다.
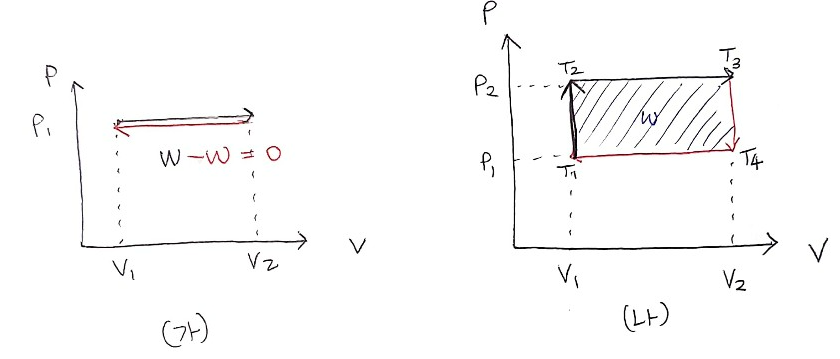
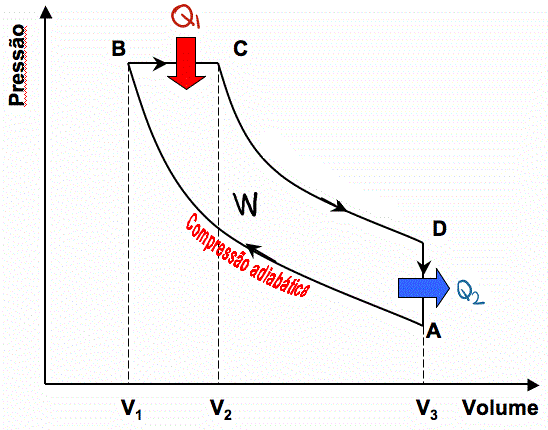
(가) 그래프와 같이 처음 상태로 되돌아오면 한 일의 양이 0이 되어버린다. 그렇기 때문에 (나) 그래프처럼 면적이 생기는 순환 과정을 거쳐야 열기관이 의미 있는 일(W)을 할 수 있다.
검은색 선 과정은 전체적으로 보면 부피도 늘어나고 온도도 증가하고 있으니 열 Q1를 흡수하는 과정이다.
빨간색 선 과정은 전체적으로 보면 부피가 줄어들고 온도가 감소하고 있으니 열 Q2를 방출하는 과정이다.
이처럼 순환 과정을 거쳐 그래프 면적(=열기관이 하는 일)이 생기려면 어쩔 수 없이 열 Q2를 방출해야 한다.
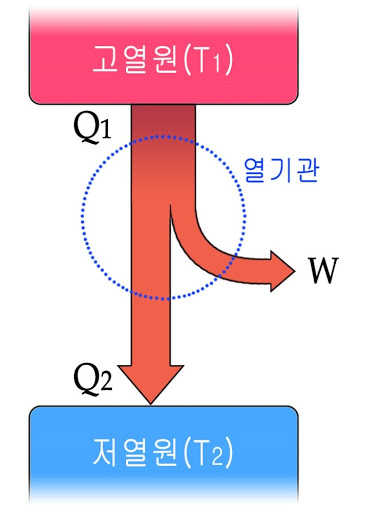
어쨌든 열기관이 순환 과정을 거쳐 일을 하기 위해서는 흡수한 열의 일부가 버려져야만 한다는 사실을 알겠다. 열기관에서는 버려지는 열이 저열원으로 이동한다. 그렇다면 버려지는 열이 저열원으로 가지 않고 자동으로 고열원으로 간다면 어떤가. 하지만 이런 일은 발생하기 어렵다. 열은 스스로 저온에서 고온으로 이동하지 않기 때문이다. 뭔가 추가적인 일을 해준다면 고온에서 저온으로 열이 이동할 수는 있다. 그러나 열효율을 최대화하기 위해 쓸데없는 일을 한다는 것 자체가 효율을 떨어뜨리는 모순이 되어버린다.
즉, 열효율 100%인 열기관은 열역학 제1법칙을 위배하지 않더라도 존재할 수가 없다. 에너지가 보존되는 큰 틀 안에서의 에너지의 흐름에도 일련의 법칙이 정해져 있기 때문이고, '열역학 제2법칙'이 그 흐름 방향을 결정한다.
열기관에서 표현되는 열역학 제2법칙
①열은 자연스러운 이동 방향은 고온에서 저온으로
②열을 모두 일로 바꾸는 것은 불가능하다.
③열효율이 1인 열기관은 없다.
④버려지는 열은 0이 될 수 없다.
2) 카르노기관
카르노기관은 이론적으로 열효율이 제일 높은, 굉장히 이상적인 열기관이다. 열효율은 다음과 같다.
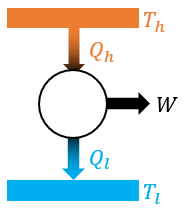
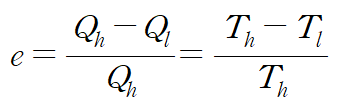
저열원의 절대 온도가 0K 또는 고열원의 절대 온도가 ∞가 될 수 없으므로, 카르노기관의 열효율 역시 100%가 될 수 없다.
카르노기관 열효율 증명
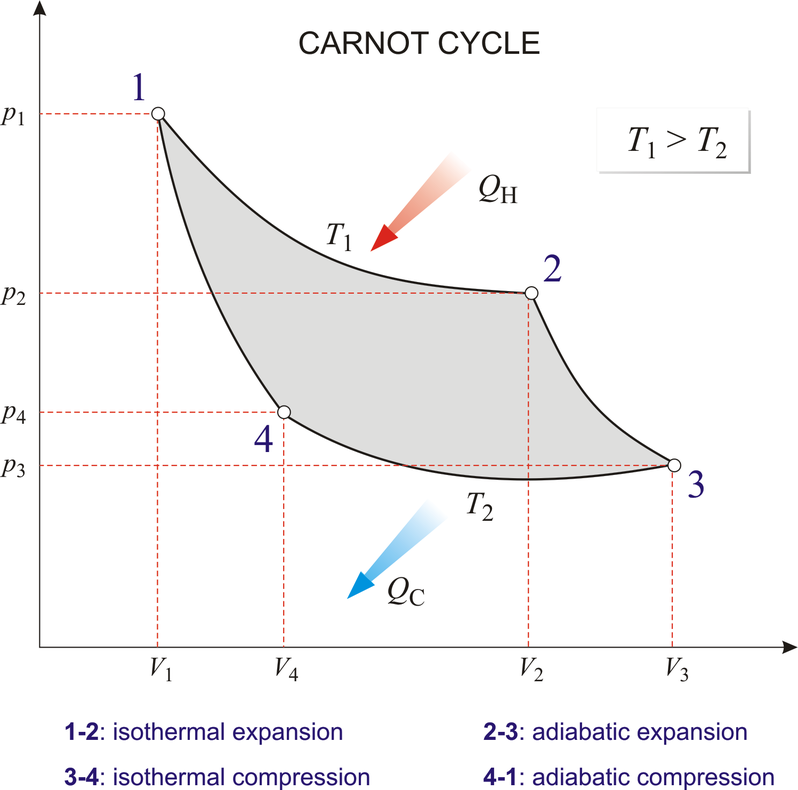
각 단계를 살펴보면 등온 팽창 과정 (1→2) 동안 기체가 팽창하면서 온도가 T1인 고열원으로부터 열 QH를 흡수하고 단열 팽창 과정 (2→3)에서 외부와의 열 접촉이 차단된 상태로 기체의 온도가 T2가 될 때까지 팽창한다. 다음 등온 압축 과정 (3→4)을 통해 온도가 T2인 저열원으로 열 QC를 방출하면서 압축되고 마지막으로 단열 압축 과정 (4→1)을 통해 외부와의 열 접촉이 차단된 상태로 기체의 온도가 T1가 될 때까지 압축되어 처음 1번 상태로 되돌아간다.
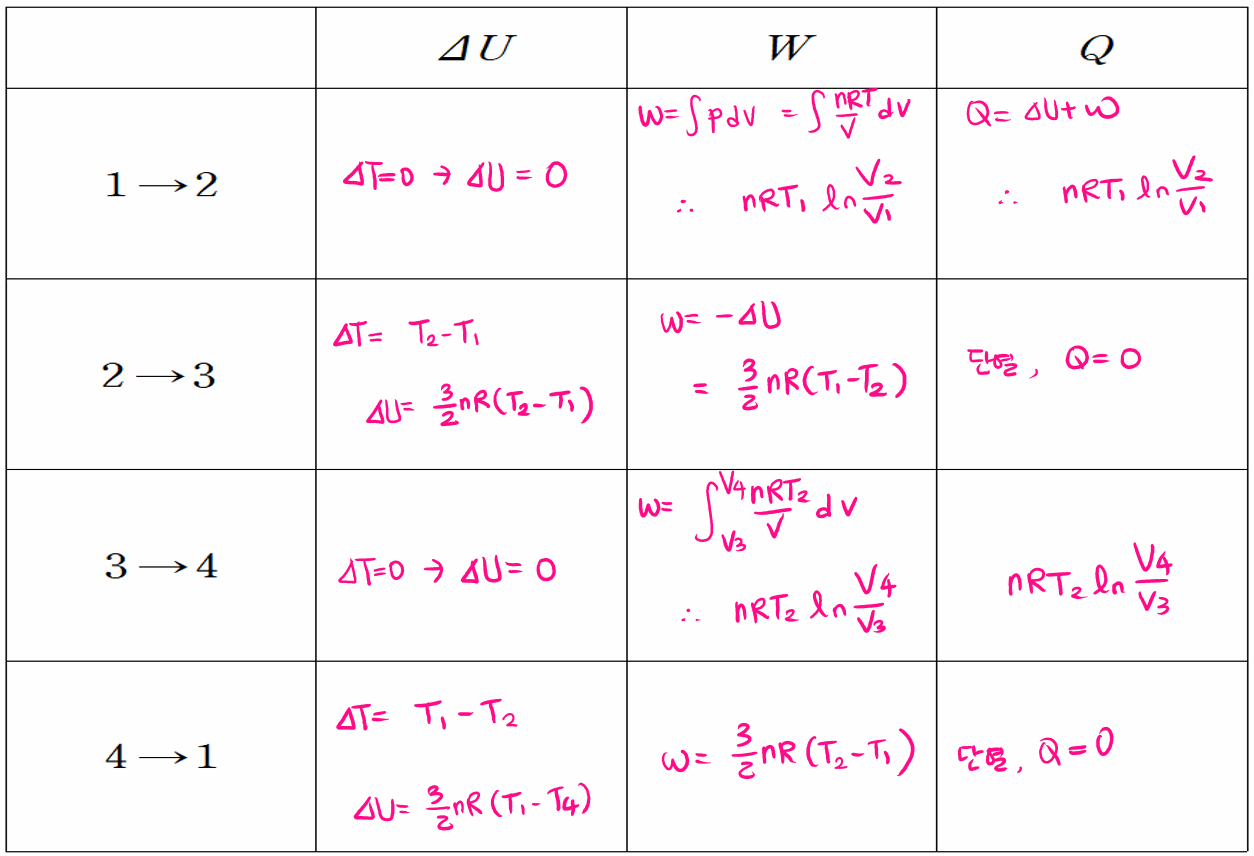
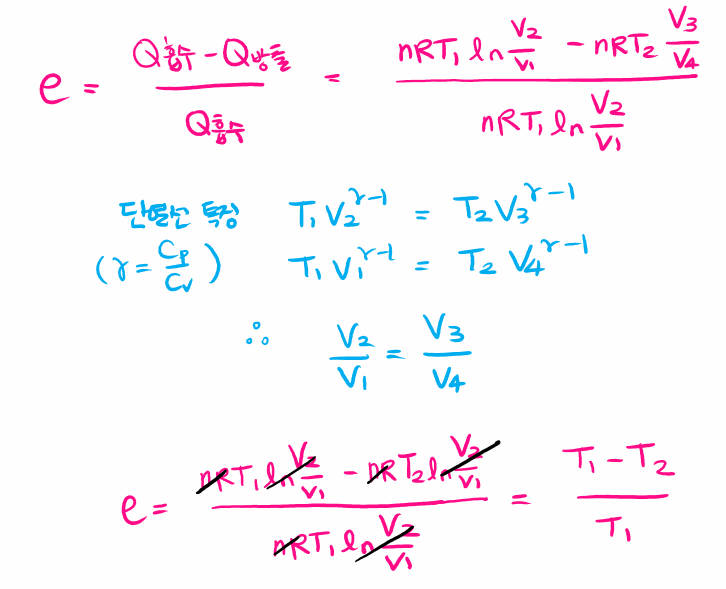
3. 엔트로피의 정량적 접근
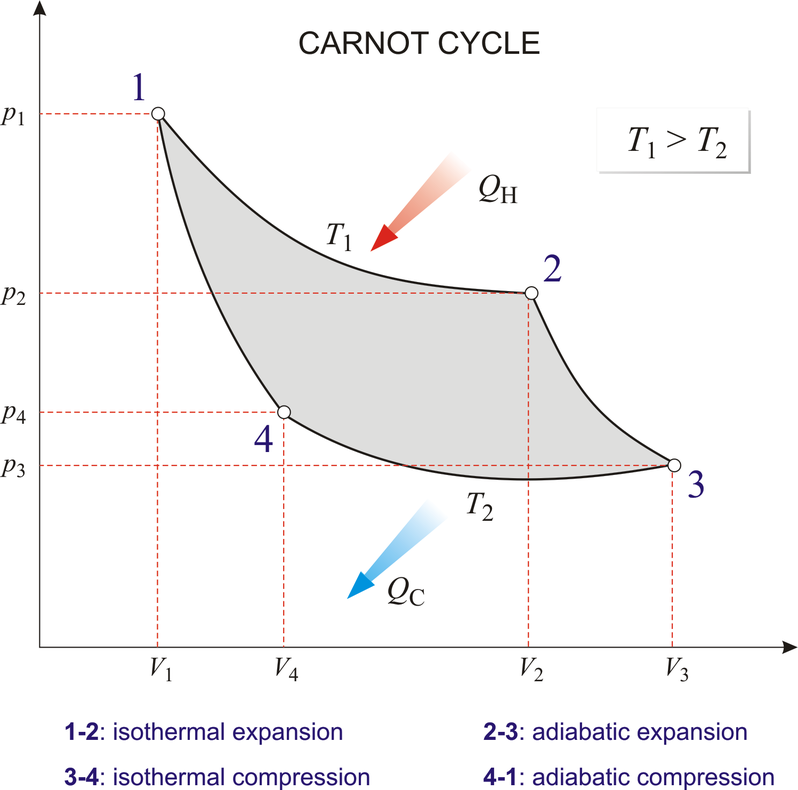
카르노 순환에서 내부 에너지처럼 처음 값과 나중 값이 같게 정의되는 물리량이 있다.
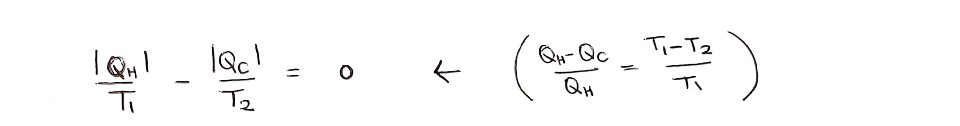
위의 식을 일반화하면
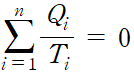
변수를 더욱 미소 단계로 나누면 다음과 같이 적분으로 나타낼 수 있다.
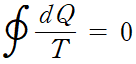
이것은 선 적분이 경로에 무관하다는 것을 나타낸다. 스토크스 정리를 연상하지 않는가?
경로에 상관없는 보존력과 스토크스 정리

따라서 Q/T의 변화량은 어떤 열역학 과정을 거치든 간에 처음 상태와 나중 상태가 같다면 같은 값으로 정의된다. 이 새롭게 정의된 상태함수 Q/T를 '엔트로피'라 한다.
S(엔트로피) = Q/T
엔트로피는 계에 열이 출입함에 따라 수반되는 양으로 계가 열을 흡수하면(Q>0) 증가하고(S>0) 열을 방출하면(Q<0) 감소하는(S<0) 양이다. 엔트로피를 이용하여 온도가 높은 물체에서 낮은 물체로 열이 이동하는 자연적인 현상을 분석해 보자.

높은 온도 TH인 물체에서 낮은 온도 TC인 물체로 열 Q가 이동할 때 엔트로피 변화는
△S = -Q/TH + Q/TC
TH > TC 이므로 위 식에 의거하면 항상 계의 엔트로피 변화량은 양수값이고 이는 엔트로피는 증가하는 방향으로 전개됨을 뜻한다.
이 세상 모든 시스템은 총 엔트로피가 증가하는 방향으로 작동한다.
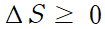
엔트로피 변화가 0인 것은 카르노 기관과 같은 이상적인 상황에 해당된다.
열기관에서 버려지는 열이 있어야 함을 엔트로피로 설명하기
열효율이 1인 열기관은 열역학 제1법칙을 만족하지만, 열역학 제2법칙을 만족하지 못한다. 버려지는 열이 0이 되면 열효율이 1이 될 수 있지만, 그렇게 돼버리면 전체 계의 엔트로피가 음의 값을 가져버린다. 전체 계 엔트로피의 변화는 항상 양의 값을 가져야만 하므로 버려지는 열은 0이 되어선 안된다.
카르노기관보다 높은 열효율을 갖는 열기관을 만들 수 없는 이유
2023.04.25 - [대학물리학 조각] - [열역학] 카르노기관보다 높은 열효율을 갖는 열기관의 모순
gooseskin.tistory.com
4. 기체의 자유 팽창
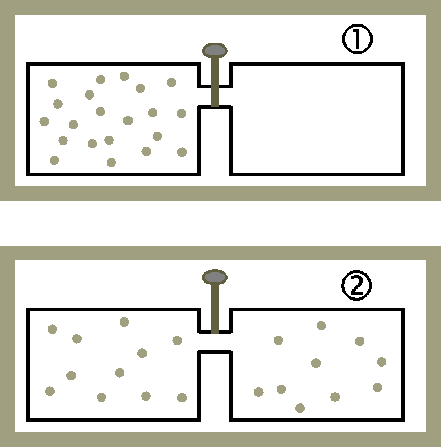
잠금장치가 열리면 왼쪽 기체가 오른쪽으로 퍼지며 고루 분포하게 된다. 이때 엔트로피 변화를 알아보자.
이때 전체 계가 단열되어 있다고 하자. 그렇다면 계에 출입한 열 Q = 0이고, 기체가 일을 하지 않으므로 W = 0 이어서(기체 분자가 밀어낼만한 물체, 가령 피스톤 같은 것이 없는 상황) 열역학 제1법칙에 의해 내부 에너지 변화도 없다.(△U=0)
자유 팽창하는 기체의 엔트로피 변화를 구해보도록 하자.
자유 팽창 과정은 처음 상태와 나중 상태는 알 수 있으나 그 중간에 어떠한 상태들을 거치는지 알 수 없다.
그러나 엔트로피는 열역학 과정이 어떠한 경로를 거치든 상관없이 같은 상태에 도달하면 같은 값을 가지므로 자유 팽창과 비슷한 열역학적 과정을 이용하면 전체 엔트로피를 구할 수 있다.
기체의 처음과 나중의 온도가 같으므로 등온 과정을 이용하여 n몰의 이상 기체가 자유 팽창을 통해 계의 부피가 2배가 되었을 때의 엔트로피 변화량을 구할 수 있다.

기체가 자유 팽창 시 엔트로피가 증가함(△S(nRln2)>0)을 확인할 수 있다.
5. 통계적 엔트로피

앞에서는 열의 출입과 관련된 형태로 엔트로피의 변화를 정의하였다. 그런데 엔트로피를 열의 출입과 무관한 형태인 통계적 관점으로 정의하기도 한다. 자연 현상의 방향성을 상태수와 겹침수와 같은 확률적인 문제로 접근하여 열역학 제2법칙을 설명하기도 한다.
S = klnΩ (Ω=계의 겹침수)
통계적 엔트로피 정의와 열역학적 엔트로피 정의는 표현 형태가 다를 뿐 동일한 양을 뜻한다.
댓글 없음:
댓글 쓰기