수학 기호 이야기 원래는 뺄셈을 뜻했던 나눗셈 기호÷

출처 : GIB

더하기에 빼기가 있다면, 곱하기에는 나누기가 있다. 사칙연산 중에서 어렵기로 따지자면 가장 어려운 게 바로 이 나눗셈이다. 곱셈이 똑같은 수를 몇 번 더하느냐를 간단히 나타낸 것이라면, 나눗셈은 어떤 수에서 똑같은 수를 몇 번 뺄 수 있느냐를 말한다.

나눗셈을 나타내는 방법은 다양하다. 일단 분수가 바로 나눗셈을 뜻한다. 가로로 길쭉한 선 위와 아래에 각각 숫자나 문자를 쓰면, 위의 것을 아래의 것으로 나누라는 뜻이 된다. 혹은 a/b와 같이 쓰는데, 경우에 따라서는 /의 방향이 좌우로 바뀌기도 한다. 두 수의 비를 나타내는 : 역시 나눗셈을 나타내는 기호다. 4:5라는 비의 값은 4를 5로 나눈 값을 말한다.

뭐니 뭐니 해도 나눗셈을 나타내는 기호로 가장 대표적인 건 ÷다. 학년이 높아질수록 거의 쓰지 않지만, 가장 먼저 산수를 배울 때 주로 사용하는 기호다 보니 나눗셈이라고 하면 으레 이 기호가 떠오른다. 과연 어떤 과정을 거쳐 ÷가 나눗셈을 나타내는 대표적인 기호가 됐는지 알아보자.

세로로 계산하는 나누기의 등장

초등학교에서 기호를 이용한 나눗셈 풀이법을 배운다. 세로로 숫자를 써 가면서 나눗셈의 답을 구하는 것이다. 예를 들어 24 나누기 8은 다음과 같다.

나누는 과정이 분명히 드러나 처음 나누기를 배울 때 편리하게 셈을 익힐 수 있다.

이런 나누기 기호 는 언제 처음 사용됐을까? 이 기호의 원조는 독일의 수학자 마이클 슈티펠의 책에서 처음 등장한다. 슈티펠은 1544년 나온 <산술백과>에서 24 나누기 8을 ‘8)24’ 또는 ‘8)24(’로 나타냈다.

나누기 기호 를 처음 사용한 독일의 수학자 마이클 슈티펠의 책 <산술백과>(1544)

슈티펠의 나누기 기호는 ‘ )’로, 기호 의 일부에 해당한다. 그렇다면 나뉘는 수 위에 쓰이는 선은 어떻게 생긴 걸까? 그 기원은 분명히 드러나 있지 않지만, 나뉘는 수를 분명하게 표시하기 위해 훗날 슈티펠의 기호 )위에 선 을 덧붙여 기호가 만들어진 것으로 추정되고 있다. 만약 슈티펠의 기호를 그냥 사용할 경우 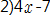이라는 식이 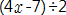를 말하는 건지, 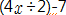을 말하는 건지 정확히 알 수가 없기 때문이다.

유럽에서는 빼기로 쓰이던 ÷

재미있게도 현재 가장 많이 쓰이고 있는 기호 ÷는 나누기 기호로 정착되기 전, 이미 많은 수학자들에 의해 다른 뜻으로 사용되고 있었다. 특히 유럽 대륙과 유럽 북단에 있는 반도 스칸디나비아의 수학자들은 ÷를 뺄셈 기호로 오랫동안 사용했다. 심지어 스칸디나비아의 몇몇 국가에서는 이 기호를 20세기까지 빼기로 사용했다. 하지만 영어를 사용하는 국가에서는 이 기호를 항상 나누기를 나타내는 것으로 사용해 왔다.

기호를 비율과 나누기를 나타내기 위해 사용한 독일의 수학자 라이프니츠 출처 : 위키미디어

÷는 1659년 스위스의 수학자 존 란의 책 <대수학>에서 처음 나누기 기호로 사용됐다. 란은 나누기 기호뿐만 아니라 ‘그러므로’를 뜻하는 수학 기호 ∴도 처음 사용한 것으로 잘 알려져 있다. 일부에서는 이 책을 편집한 존 펠이 ÷를 나눗셈 기호로 사용한 장본인이라고 생각하기도 한다.

스위스의 수학자 존 란이 자신의 책 <대수학>에서 처음으로 나누기 기호를 사용한 페이지
출처 : 위키미디어

그렇다면 ÷는 왜 나누기를 나타내는 데 쓰였을까? 한 가지 주장에 따르면, 여기에는 상형문자의 원리가 반영돼 있다. 상형문자는 대상의 모양을 본떠 나타내는 문자다. 말하고자 하는 대상의 모양과 최대한 비슷하게 보여줘서 이해하기 쉽게 만드는 것이다. 아마 처음에는 그림문자로 시작됐다가 점차 기호로 바뀌었을 것이다. 예를 들어 ‘해’를 뜻하는 한자 日(날일)은 해의 모양을 본떠 만들어졌다.

÷ 기호에서 가로막대 ─ 위아래의 두 점 ·은 수를 나타낸다. 예를 들어 35÷23은 과 같은 분수 형태로 나타낼 수 있는데, 기호 ÷는 이 분수의 모양을 나타낸 것으로 볼 수 있다는 것이다. 가로막대 ─ 위에 있는 35와 아래에 있는 23을 각각 ·으로 바꾸어 쓰면 바로 나누기 기호 ÷가 된다.

하마터면 빼기로 사용할 뻔한 ÷ 기호가 오늘날 나눗셈을 나타내는 기호로 자리 잡기까지는 이런 흥미로운 역사가 있다.

사이언스올