세상에서
가장 큰 수는 무엇일까? 생각해 보면 가장 큰 수는 있을 수가 없다. 아무리 큰 수를 생각해도 거기에 1만 더하면 더 큰 수가 되기 때문이다.
이처럼 수가 커지는 데는 한계가 없다. 그래서 수학에서는 무한대라는 개념을 만들었다. 말 그대로 한계가 없이 영원히 커지는 상태를 말한다.
상상하기 어려운 개념이지만, 이 개념을 나타내는 기호 역시 있다. 일반적인 숫자로는 나타낼 수 없기 때문에 따로 기호를 만든 것이다.
뒤늦게 나타난 무한대 기호
무한대라는
개념은 오래 전부터 희미하게 있었다. ‘제논의 역설’로 유명한 그리스 철학자 제논도 무한대라는 수학적인 개념을 언급한 바 있다. 고대 인도의
수학에도 무한대라는 개념이 등장한다.
무한대를
나타내는 기호 ∞는 그로부터 약 2000년 뒤에야 등장했다. 1655년 영국의 수학자 존 월리스가 쓴 책에 처음 등장한 것이다. 월리스는 원래
영국 케임브리지대에서 신학을 공부한 성직자였지만, 수학과 물리학에 관심을 갖고 다시 공부해 1649년 영국 옥스퍼드대의 기하학 교수가 된
인물이다. 결과적으로 그가 수학으로 전공을 바꾼 일은 굉장히 잘한 일이었다. 이탈리아의 수학자 카발리에리나 프랑스의 수학자이자 철학자인
데카르트의 생각을 이어 극한 개념을 수학적으로 발전시켰기 때문이다.

우주의 크기처럼 무한대를 나타낼 때는 어떤 기호를 쓸까? 무한대를 나타내는 기호 ∞는 1655년 영국의 수학자 존 월리스의 책에 처음 등장했다. 출처: GIB
이뿐만
아니라 월리스는 천문학, 식물학, 음악 등 다방면에 재능을 보였는데, 그중에서도 암호 해독에 두각을 나타냈다. 월리스는 ∞를 무한대 기호로
선택한 이유를 따로 설명하지 않았지만, 사람들은 1000을 나타내는 옛 로마 숫자 CI 또는 C 에서 유래했을 것으로 추측하고 있다. 이는
1000이 옛 로마뿐만 아니라 당시 영국에서도 무한대를 의미할 만큼 매우 큰 수였기 때문이다.
CI
나 C 의 모양도 ∞와 매우 비슷하다. 한편, ∞가 그리스의 알파벳 가장 마지막 글자인 오메가 ‘ω’에서 유래했다는 설도 있다. 이는 오메가가
흔히 ‘끝’을 상징하는 알파벳으로 사용되고, ∞와도 그 모습이 닮아서다.

무한대 기호는 디자인 요소로도 많이 쓰인다. 출처 GIB
무한의 개념을 수학적으로 증명한 칸토어
무한대
기호가 등장했음에도, 문제는 있었다. 그때까지도 무한이라는 개념이 수학적으로 엄밀하게 완성되지 않았던 것이다. 보통은 수학 개념이 먼저 정립된
뒤에야 이를 나타내는 기호가 여러 변천 과정을 거쳐 오늘날과 같은 모양에 이른다. 그러나 무한의 경우에는 그 순서가 정반대다. 기호 ∞가 먼저
자리를 잡은 다음, 약 200년이 지난 뒤에야 무한의 개념을 수학적으로 엄밀하게 정의할 수 있었던 것이다.
기호가
등장한 뒤에도 무한은 그저 인간이 셀 수 있는 한계를 넘어선 매우 큰 수 정도로 여겨질 뿐이었다. 예를 들어 18세기 스위스의 수학자 레온하르트
오일러는 무한이 수의 하나라고 했지만, 무한의 개념이 무엇인지, 어떤 성질을 갖고 있는지 확실히 설명하지 못했다. 자신의 책
<대수학>에서는 아무 설명도 없이 10을 무한이라고 썼다.
당시
무한은 인간의 한계를 초월한 신의 영역으로 여겨지기도 했다. 무한을 분석하거나 규명하는 게 수학계의 금기로 여겨질 정도였다. 심지어 ‘수학의
황제’라 불리는 독일의 수학자 가우스조차 ‘무한이란 수학적으로 가치가 없다’고 말하기도 했다.
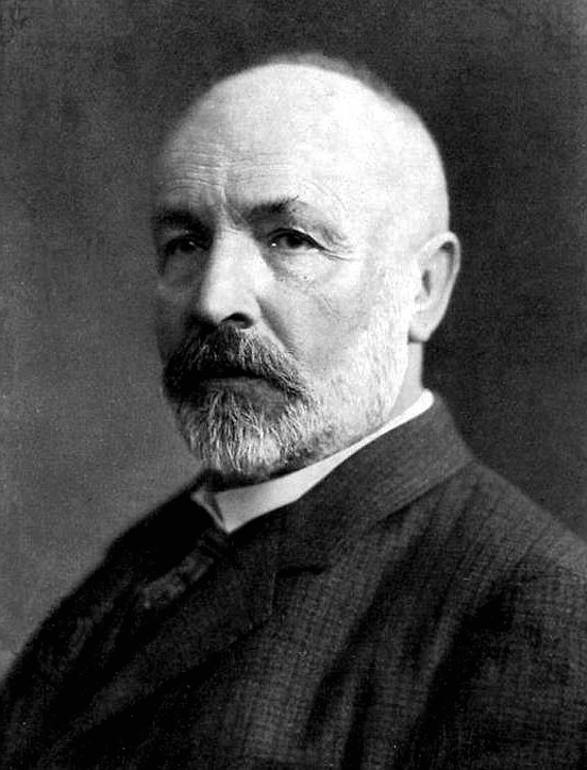
게오르그 칸토어 출처 : 위키미디어
19세에
이르러서야 수학의 금기에 도전한 수학자가 등장한다. 바로 독일의 수학자 게오르그 칸토어다. 그는 1878년 집합론을 창시하며 ‘무한’이란 난제의
돌파구를 찾는다. 칸토어는 집합론을 이용해 무한의 개념을 수학적으로 정의하며, a1, a2, a3, …과 같은 수열에서 아무리 큰 수 x를
골라도 이 수보다 큰 수는 반드시 존재한다고 발표했다. 하지만 이런 주장은 당시 수학자들에게 쉽게 받아들여지지 못했다. 스승인 크로네커조차
새로운 생각을 받아들이지 못하고 칸토어가 수학계에 도전한다며 독설을 퍼부었다.
칸토어는
홀로 수많은 비판자와 맞서 외로운 투쟁을 벌였지만, 결국 정신적 압박을 이기지 못하고 정신병원을 오가는 생활을 하게 된다. 그러다 1918년,
한 정신병원에서 숨을 거두고 말았다. 그래도 다행히 죽기 전에 스승인 크로네커와 화해하고, 업적을 인정받았다.
“수학의
본질은 자유에 있다”고 주장한 칸토어의 말처럼, 상식을 뒤집어 생각을 전환할 때 위대한 발견을 할 수 있다는 사실을 기억하길 바란다.
사이언스올
댓글 없음:
댓글 쓰기