수학 기호 이야기 딱 보면 아는 삼각형 기호 △

건물을 지을 때 무엇이 가장 중요할까? 아름다움이나 기능도 중요하지만, 아무래도 안전이 가장 중요하다. 교량과 같은 구조물도 마찬가지다. 지진과 같은 자연재해가 와도 건물이 무사히 서 있어야 인명 피해를 줄일 수 있다.

그러기 위해서는 외부의 힘에 가장 잘 견디는 구조로 건물을 지어야 한다. 재미있게도 수학에서 가장 기본적인 도형이 바로 그런 성질을 지니고 있다. 삼각형이다. 삼각형은 선 3개로만 만들 수 있는 간단한 도형이지만, 외부에서 받는 힘에 가장 잘 버틴다.

그래서 건축물에는 삼각형 구조가 많이 쓰인다. 대표적인 게 트러스 구조다. 직선 부재를 여러 개 연결해 삼각형 구조가 계속 이어지게 만들어 구조물의 무게를 지탱한다. 지진에 대비해 건물을 보강할 때도 삼각형 구조물을 덧댄다.

미국 UC버클리의 한 건물은 외벽에 덧댄 삼각형 골조로 지진에 대비했다. 출처 위키미디어

수학을 좋아하는 사람이라면 이런 건물이 보일 때 삼각형을 떠올릴 것이다. 혹은 삼각형과 관련된 다른 개념까지 생각의 폭을 넓힐 수도 있다. 삼각형 모양의 구조를 보고 삼각형을 떠올리는 게 너무나 당연한 것처럼 수학에서 삼각형을 나타내는 기호도 너무나 당연해 보인다. 바로 △다. 굳이 누가 만들었어야 했나 하는 생각이 드는 기호지만, 처음 쓴 사람은 있다. 함께 알아보자.

피에르 헤리곤의 책 <수학 강좌> 출처 : 위키피디아

삼각형을 보면 떠오르는 기호들

삼각형의 생김새를 본뜬 △의 원조는 프랑스의 수학자 피에르 헤리곤이다. 꼭짓점이 A, B, C인 삼각형을 간단히 △ABC라고 나타낸다. 그는 1644년 삼각형을 표기하기 위해 △abc를 사용했다. 꼭짓점을 나타내는 영어 알파벳이 소문자라는 점이 지금과 다르지만, 오늘날도 여전히 똑같은 기호를 가지고 삼각형을 나타낸다.

삼각형을 공부하면서 나오는 다른 기호도 헤리곤의 만든 게 많다. 우리는 각도를 표기할 때 ∠를 사용한다. 이 기호는 도형의 각을 의미하는 동시에 ∠AOB=60˚처럼 각의 크기를 나타낼 때도 쓰인다. 한눈에 봐도 각의 모양을 형상화한 이 기호는 헤리곤이 1644년 자신의 책 <수학 강좌>에서 처음 사용했다. 그는 10년 전인 1634년에 동일한 책 <수학 강좌>에서는 각을 표현하기 위해 ‘<’라는 기호를 썼었다.

그런데 왜 기호 ∠를 새로 만든 것일까? 17, 18세기에 ‘<’는 각을 표현하는 기호로 종종 사용됐다. 하지만 영국의 수학자 토마스 해리엇이 세상을 떠난 뒤 <대수방정식 풀이에 응용되는 해석학적 기술>(1631)이 출간되면서 문제가 생긴다. 이 책에서 각을 표현하는 기호와 꼭 닮은 부등호(<,>)가 사용되면서 혼동을 일으켰기 때문이다.

이런 이유로 각을 표현하는 기호 <가 점차 사라지게 되자, 1644년 피에르 헤리곤이 각을 표현하기 위해 ∠를 처음 사용한 것이다. ∠가 각을 표현하는 기호로 정착되기 전에는 ∠를 두 개 겹친 기호(∠∠)나 ∠를 180˚회전시킨 기호 ⦣ 또는 ∧, ∡가 사용되기도 했다. 그러다가 1657년 영국의 수학자 윌리엄 오트레드가 기호 ∠를 사용하면서 지금까지 쓰이고 있다.

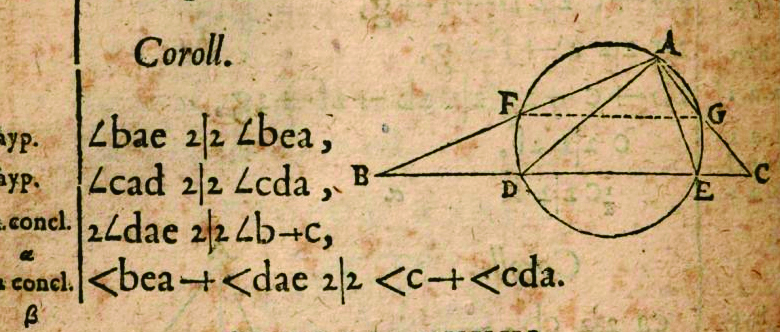
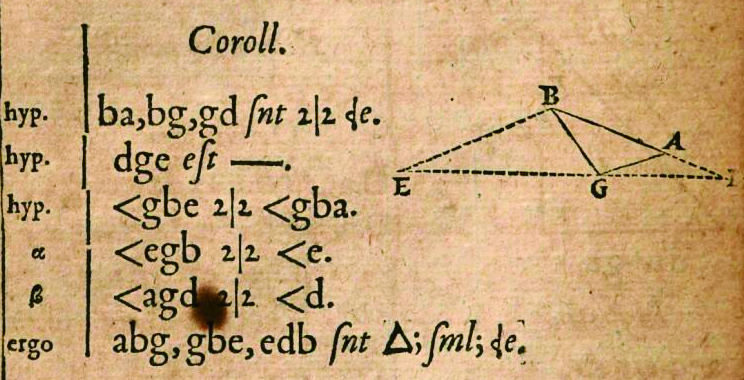
∠, △가 등장한 <수학 강좌>의 일부. 출처 : 위키피디아

헤리곤이 처음 만들어 현재까지 쓰이고 있는 기호는 또 있다. 헤리곤은 1634년 <수학 강좌> 책에서 두 직선이 서로 수직임을 나타내는 기호 ‘⊥’를 처음으로 사용하기도 했다. 각도, 삼각형, 수직을 표기하기 위해 여러 수학자들이 기호를 만들었지만, 현재까지 살아남은 건 헤리곤의 기호다.

백과사전식 수학 교과서를 펴낸 피에르 헤리곤

사실 피에르 헤리곤은 우리에게는 좀 생소한 수학자다. 그런데 알고 보면 <수학 강좌>라는 6권의 수학 교과서 시리즈를 통해 수학 기호의 발달에 중요한 역할을 한 사람이다. <수학 강좌> 시리즈는 대수학이나 기하학과 같은 순수수학은 물론 군사, 기계, 지리, 항해술 등에 쓰이는 수학도 다루고 있다. 즉, 17세기의 백과사전식 수학 교과서였던 셈이다.

이 책은 1634년에 처음 세상에 나온 뒤, 1644년에는 두 번째 판이 출간될 정도로 큰 인기를 모았다. 수학 논문이나 수학자끼리 주고받은 편지에도 이 책이 언급됐을 정도로 널리 읽혔다.

독일의 수학자 라이프니츠는 한 편지에서 <수학 강좌>를 언급하며 수학기호의 중요성에 대해 썼다. 출처 : 위키피디아

헤리곤은 ∠, △, ⊥ 외에도 <수학 강좌> 시리즈를 통해 여러 수학 기호를 선보이며 기호를 쓰는 것이 얼마나 유용하고 중요한지 강조했다.

그 결과 헤리곤은 누구보다 수학 기호의 중요성을 일찍 깨닫고 이를 알리기 위해 노력한 수학자로 손꼽히고 있다. 만약 헤리곤이 아니었다면, 우리는 삼각형이나 각도 같은 간단한 개념도 번거롭게 말로 나타내야 했을지도 모른다.

사이언스올