수학 기호 이야기 간단하고 다재다능한, 점(․)

유럽 여행을 가보면 헷갈리는 경험을 할 수 있다. 숫자 읽기 때문이다. 1.234라고 씌어 있어서, 1점234인 줄 알았는데, 알고 보면 1234를 나타내고 있다. 우리나라와 대부분의 영어권 국가에서는 소수점을 ‘.’으로 나타내고, ‘,’로 자릿수를 구분한다. 유럽이나 남아메리카에서는 그 반대로 쓰는 나라가 많다.

오늘날 우리는 글을 읽을 때마다 마침표 기호를 접한다. 출처: 동아사이언스

연필로 종이에 한 번 콕 찍어주기만 하면 되는 기호인 점은 쓰기가 편해서인지 용도가 매우 다양하다. 일단 글을 쓸 때는 마침표(.)와 가운뎃점(․)로 쓰인다. 마침표는 문장을 끝맺는 기호고, 가운뎃점은 단어를 여러 개 나열할 때 사이에 넣는 점이다. 점 세 개를 연달아 쓰면 줄임표(…)가 된다.

수학에서도 점은 여러 가지 기호로 쓰인다. 앞서 언급한 소수점을 시작으로 점이 어떻게 수학 기호에 들어왔는지 살펴보자.

혁신적인 소수 표현법

16세기 네덜란드의 수학자이자 기술자였던 시몬 스테빈(1548~1620)은 군대에서 군자금을 관리했다. 그의 업무 중 하나는 은행에서 빌린 돈을 이자와 함께 갚는 일이었는데, 이자 계산에 늘 골치를 썩었다. 그가 이자 계산 때문에 유독 힘들어 했던 이유는 당시에는 소수가 없어서 이자율을 분수로 계산해야 했기 때문이다. 이자가 1/10일 때에는 계산이 간단했지만 1/11 , 1/12 일 때는 계산이 복잡했다.

네덜란드의 수학자 시몬 스테빈.
출처: 위키미디어

이자를 간단히 계산할 수 있는 방법이 없을까 밤낮으로 궁리하던 스테빈은 어느 날 좋은 생각이 떠올랐다. 바로 이자의 분모를 10, 100, 1000 등 10의 거듭제곱 꼴로 생각하고 계산하는 것이었다. 예를 들어 이자율이 1/11인 경우 거의 비슷한 9/100로 계산하고, 1/12인 경우 거의 비슷한 8/100로 대신 계산을 하면 훨씬 간단하게 이자를 계산할 수 있다.

스테빈의 발견은 복잡한 분수 계산에 속 썩지 않고도 누구나 간단히 이자를 계산할 수 있는 결과를 가져왔다. 그래서 그는 1584년, 이자가 1/10에서부터 5/100까지의 여러 가지 경우를 계산한 표를 만들어 책을 내기도 했다.

스테빈은 여기에서 그치지 않고 두 소수의 크기를 쉽게 비교하는 방법은 없을지 고민했다. 사실 그의 이자율 표에는 56789/100000처럼 분모와 분자가 모두 큰 수인 경우가 많았다. 이런 분수 꼴은 어느 쪽이 더 큰지 한눈에 알아보기 어렵다는 단점이 있었다. 이를 해결하기 위해 스테빈은 분모에 0이 몇 개 있는지, 분자가 몇 자리 수인지 동시에 알아볼 수 있는 방법을 고안했다. 그리고 1585년 <소수에 관하여>란 자신의 책에 최초로 소수 개념과 표기법에 대해 설명했다. 그는 이 책에서 소수의 각 자릿수를 ⓪ , ①, ②, ③, …과 같은 원문자의 형태로 나타냈다.

⓪ ① ② ③

12.345 → 12⓪ 3① 4② 5③ 또는 12 3 4 5

또한 스테빈은 두 소수의 곱도 오른쪽과 같이 구했다. 이 식은 0.000378과 0.54를 곱해 0.00020412가 나온 것을 의미한다. 지금 보면 굉장히 독특하고 복잡해 보이지만 당시로서는 혁신적인 표기법으로 주목을 받았다.

하지만 사실 스테빈의 원문자 표기법은 쓰기에 불편하다는 단점이 있었다. 이에 스위스의 수학자인 요스트 뷔르기가 최초로 점을 사용해 수의 자리를 표기했다. 현재 사용하는 ‘12.345’를 12.3.4.5와 같이 여러 개의 점을 사용해 나타낸 것이다.

현재와 같은 소수점을 최초로 쓴 사람은 독일의 수학자 크리스토퍼 클라비우스다. 하지만 당시 그의 표기는 널리 쓰이지 못하다가 1617년이 되어서야 영국의 수학자 존 네이피어 덕분에 본격적으로 사용되기 시작했다. 네이피어는 자신의 책 <막대 계산술>에서 소수에 대해 설명하면서 소수점을 사용했다.

무한을 나타내는 점

이번에는 점의 위치를 살짝 바꿔 보자. 소수점처럼 아래쪽이 아니라 조금 올려서 가운데에 점을 찍으면 뜻이 달라진다. 이때는 점이 곱하기를 나타내는 기호가 된다. a․b는 a×b라는 뜻이다. 문자를 쓸 때는 생략해서 그냥 붙여 쓰는 일이 많지만, 엄연히 곱셈 기호로 쓰인다고 할 수 있다.

점의 위치를 더 위로 올려보자. 그러면 점은 소수점 아래에서 계속 반복되는 수를 줄여서 나타내는 용도가 된다. 0.333…, 1.23232323…과 같은 소수는 소수점 아래 어딘가에서부터 계속 똑같은 수가 반복된다. 이런 소수를 순환소수라고 한다.

순환소수를 나타내기 위해서는 순환마디의 양끝 숫자 위에 점을 찍는다. 0.33333…은 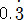으로 간단히 나타낼 수 있고, 1.23232323…은 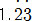과 같이 간단히 표시한다. 순환하는 마디가 길어져도 양 끝에만 두 개 찍으면 된다. 예를 들어, 0.12356435643564…는 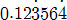가 된다.

출처: GIB

점을 찍어 순환소수를 나타낸 건 18세기 영국의 수학자 존 마쉬다. 하지만 그가 순환소수 표기법을 독창적으로 만들었다기보다는 여러 사람이 만든 기호를 점차 개량해 온 것으로 보인다. 예를 들어 18세기 존 로버트슨은 0.785785…를 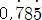로 표기하며 오늘날과 비슷하게 순환소수를 표기했다. 하지만 소수점에 쉼표(,)를 사용했다는 차이가 있다. 또한 헨리 클라크 역시 비슷한 시기에 0.641641…을 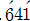로 표기했고, 이후 19세기의 수학자 로버트 포트와 재임스 프라이드 등은 0.333…을 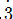으로, 샤를 데이비스와 윌리엄 펙은 0.222…를 .`2로 썼다.

이렇듯 처음에는 다양한 방식의 순환소수 표기 방법이 있었다. 이들 방법이 점차 개량되고 통합되면서 오늘날의 순환소수 표기법이 자리를 잡은 것이다.

사이언스올