녹원학원 수학과학영재교육 010-3549-5206 : 2020 AMC10A-12 문제 해설 무게중심 닮음꼴 이용

Triangle $AMC$ is isosceles with $AM = AC$ . Medians $\overline{MV}$ and $\overline{CU}$ are perpendicular to each other, and $MV=CU=12$ . What is the area of $\triangle AMC?$

$[asy] draw((-4,0)--(4,0)--(0,12)--cycle); draw((-2,6)--(4,0)); draw((2,6)--(-4,0)); label("M", (-4,0), W); label("C", (4,0), E); label("A", (0, 12), N); label("V", (2, 6), NE); label("U", (-2, 6), NW); label("P", (0, 3.6), S); [/asy]$

$\textbf{(A) } 48 \qquad \textbf{(B) } 72 \qquad \textbf{(C) } 96 \qquad \textbf{(D) } 144 \qquad \textbf{(E) } 192$

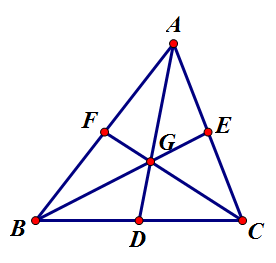
삼각형 AMC 는 AM = AC 인 이등변 삭각형 이다.
중선 MV 와 CU 는 서로 직교 한다.
MV = CU = 12 이다.
AMC 의 넓이는 ?

풀이는 보지말고 , 풀릴때 까지 혼자 풀어 보세요.

자기방식 데로 풀어보고 , 더 쉬운 방법이나 더 좋은 방법이 있으면 찾아보세요.

삼각형의 무게중심centroid 의 성질

삼각형의 무게중심 center of gravity,은 '삼각형의 세 중선이 만나는 점'이다.

삼각형의 세 중선은 반드시 한 점에서 만난다.
세 중선은 무게중심에 의해 2:1로 나눠진다.
세 중선에 의해 생기는 6개의 삼각형은 넓이가 같다.

Solution 1

Since quadrilateral $UVCM$ has perpendicular diagonals, its area can be found as half of the product of the length of the diagonals. Also note that $\triangle AUV$ has $\frac 14$ the area of triangle $AMC$ by similarity, so $[UVCM]=\frac 34\cdot [AMC].$ Thus, $\frac 12 \cdot 12\cdot 12=\frac 34 \cdot [AMC]$ $72=\frac 34\cdot [AMC]$ $[AMC]=96\rightarrow \boxed{\textbf{(C)}}.$

Solution 2 (Trapezoid)

$[asy] draw((-4,0)--(4,0)--(0,12)--cycle); draw((-2,6)--(4,0)); draw((2,6)--(-4,0)); draw((-2,6)--(2,6)); label("M", (-4,0), W); label("C", (4,0), E); label("A", (0, 12), N); label("V", (2, 6), NE); label("U", (-2, 6), NW); label("P", (0, 3.6), S); [/asy]$

We know that $\triangle AUV \sim \triangle AMC$ , and since the ratios of its sides are $\frac{1}{2}$ , the ratio of of their areas is $(\frac{1}{2})^2=\frac{1}{4}$ .

If $\triangle AUV$ is $\frac{1}{4}$ the area of $\triangle AMC$ , then trapezoid $MUVC$ is $\frac{3}{4}$ the area of $\triangle AMC$ .

Let's call the intersection of $\overline{UC}$ and $\overline{MV}$ $P$ . Let $\overline{UP}=x$ . Then $\overline{PC}=12-x$ . Since $\overline{UC} \perp \overline{MV}$ , $\overline{UP}$ and $\overline{CP}$ are heights of triangles $\triangle MUV$ and $\triangle MCV$ , respectively. Both of these triangles have base $12$ .

Area of $\triangle MUV = \frac{x\cdot12}{2}=6x$

Area of $\triangle MCV = \frac{(12-x)\cdot12}{2}=72-6x$

Adding these two gives us the area of trapezoid $MUVC$ , which is $6x+(72-6x)=72$ .

This is $\frac{3}{4}$ of the triangle, so the area of the triangle is $\frac{4}{3}\cdot{72}=\boxed{\textbf{(C) } 96}$ ~quacker88, diagram by programjames1

Solution 3 (Medians)

Draw median $\overline{AB}$ . $[asy] draw((-4,0)--(4,0)--(0,12)--cycle); draw((-2,6)--(4,0)); draw((2,6)--(-4,0)); draw((0,12)--(0,0)); label("M", (-4,0), W); label("C", (4,0), E); label("A", (0, 12), N); label("V", (2, 6), NE); label("U", (-2, 6), NW); label("P", (0.5, 4), E); label("B", (0, 0), S); [/asy]$

Since we know that all medians of a triangle intersect at the incenter, we know that $\overline{AB}$ passes through point $P$ . We also know that medians of a triangle divide each other into segments of ratio $2:1$ . Knowing this, we can see that $\overline{PC}:\overline{UP}=2:1$ , and since the two segments sum to $12$ , $\overline{PC}$ and $\overline{UP}$ are $8$ and $4$ , respectively.

Finally knowing that the medians divide the triangle into $6$ sections of equal area, finding the area of $\triangle PUM$ is enough. $\overline{PC} = \overline{MP} = 8$ .

The area of $\triangle PUM = \frac{4\cdot8}{2}=16$ . Multiplying this by $6$ gives us $6\cdot16=\boxed{\textbf{(C) }96}$

~quacker88

Solution 4 (Triangles)

As $\angle UPM = \angle VPC = 90$ , we can see that $\triangle UPM \cong \triangle VPC$ and $\triangle UVP \sim \triangle MPC$ with a side ratio of $1 : 2$ .

So $UP = VP = 4$ , $MP = PC = 8$ .

With that, we can see that $[\triangle UPM] = 16$ , and the area of trapezoid $MUVC$ is 72.

As said in solution 1, $[\triangle AMC] = 72 / \frac{3}{4} = \boxed{\textbf{(C) } 96}$ .

-QuadraticFunctions, solution 1 by ???

Solution 5 (Only Pythagorean Theorem)

$[asy] draw((-4,0)--(4,0)--(0,12)--cycle); draw((-2,6)--(4,0)); draw((2,6)--(-4,0)); draw((0,12)--(0,0)); label("M", (-4,0), W); label("C", (4,0), E); label("A", (0, 12), N); label("V", (2, 6), NE); label("U", (-2, 6), NW); label("P", (0.5, 4), E); label("B", (0, 0), S); [/asy]$

Let $AB$ be the height. Since medians divide each other into a $2:1$ ratio, and the medians have length 12, we have $PC=MP=8$ and $UP=UV=4$ . From right triangle $\triangle{MUP}$ , $MU^2=MP^2+UP^2=8^2+4^2=80,$ so $MU=\sqrt{80}=4\sqrt{5}$ . Since $CU$ is a median, $AM=8\sqrt{5}$ . From right triangle $\triangle{MPC}$ , $MC^2=MP^2+PC^2=8^2+8^2=128,$ which implies $MC=\sqrt{128}=8\sqrt{2}$ . By symmetry $MB=\dfrac{8\sqrt{2}}{2}=4\sqrt{2}$ .

Applying the Pythagorean Theorem to right triangle $\triangle{MAB}$ gives $AB^2=AM^2-MB^2=8\sqrt{5}^2-4\sqrt{2}^2=288$ , so $AB=\sqrt{288}=12\sqrt{2}$ . Then the area of $\triangle{AMC}$ is $\dfrac{AB \cdot MC}{2}=\dfrac{8\sqrt{2} \cdot 12\sqrt{2}}{2}=\dfrac{96 \cdot 2}{2}=\boxed{\textbf{(C) }96}$

Solution 6 (Drawing)

(NOT recommended) Transfer the given diagram, which happens to be to scale, onto a piece of a graph paper. Counting the boxes should give a reliable result since the answer choices are relatively far apart. -Lingjun

Solution 7

Given a triangle with perpendicular medians with lengths $x$ and $y$ , the area will be $\frac{2xy}{3}=\boxed{\textbf{(C) }96}$ .

Solution 8 (Fastest)

Connect the line segment $UV$ and it's easy to see quadrilateral $UVMC$ has an area of the product of its diagonals divided by $2$ which is $72$ . Now, solving for triangle $AUV$ could be an option, but the drawing shows the area of $AUV$ will be less than the quadrilateral meaning the the area of $AMC$ is less than $72*2$ but greater than $72$ , leaving only one possible answer choice, $\boxed{\textbf{(C) } 96}$ .

여러풀이 방식이 있군요.
자세 하게는 010-3549-5206

녹원학원 수학과학영재교육 010-3549-5206

2020년 2월 7일 금요일

2020 AMC10A-12 문제 해설 무게중심 닮음꼴 이용