그림으로 보는 수학 공식 ③ 쌓기 나무로 배우는 자연수의 합

복잡한 수학 공식도 그림으로 이해하면 머리에 쏙쏙 들어온다. 수학 공식을 알려주는 그림과 그에 얽힌 이야기를 소개한다!

자연수의 합은 ‘배열’과 ‘쌓기 나무’로!

만약 누군가 ‘홀수의 합을 구하는 공식을 설명해 보라’고 한다면 어떨까?

1부터 (2n-1)까지 홀수의 합을 구하는 공식은 n²으로 간단하지만, 그것을 설명하는 것은 쉽지 않다. 게다가 직접 증명을 하려면 수학에서 합을 나타내는 ‘시그마(Σ)’의 성질을 이용해야 하기 때문에 더 어렵다.

니코마쿠스의 그림.

하지만 위의 그림과 같은 그림 하나면 홀수의 합을 구하는 공식을 쉽게 이해할 수 있다. 이 그림은 100년 경 고대 그리스의 수학자 니코마쿠스의 그림으로, 초록색 돌과 파란색 돌을 정사각형 모양으로 배열한 간단한 그림이다. 이 그림에는 어떠한 수식도 없지만 흰 돌과 검은 돌이 각각 1, 3, 5, …(2n-1)로 홀수를 나타내고 있어, 그 합이 n²인 것을 쉽게 알 수 있다.

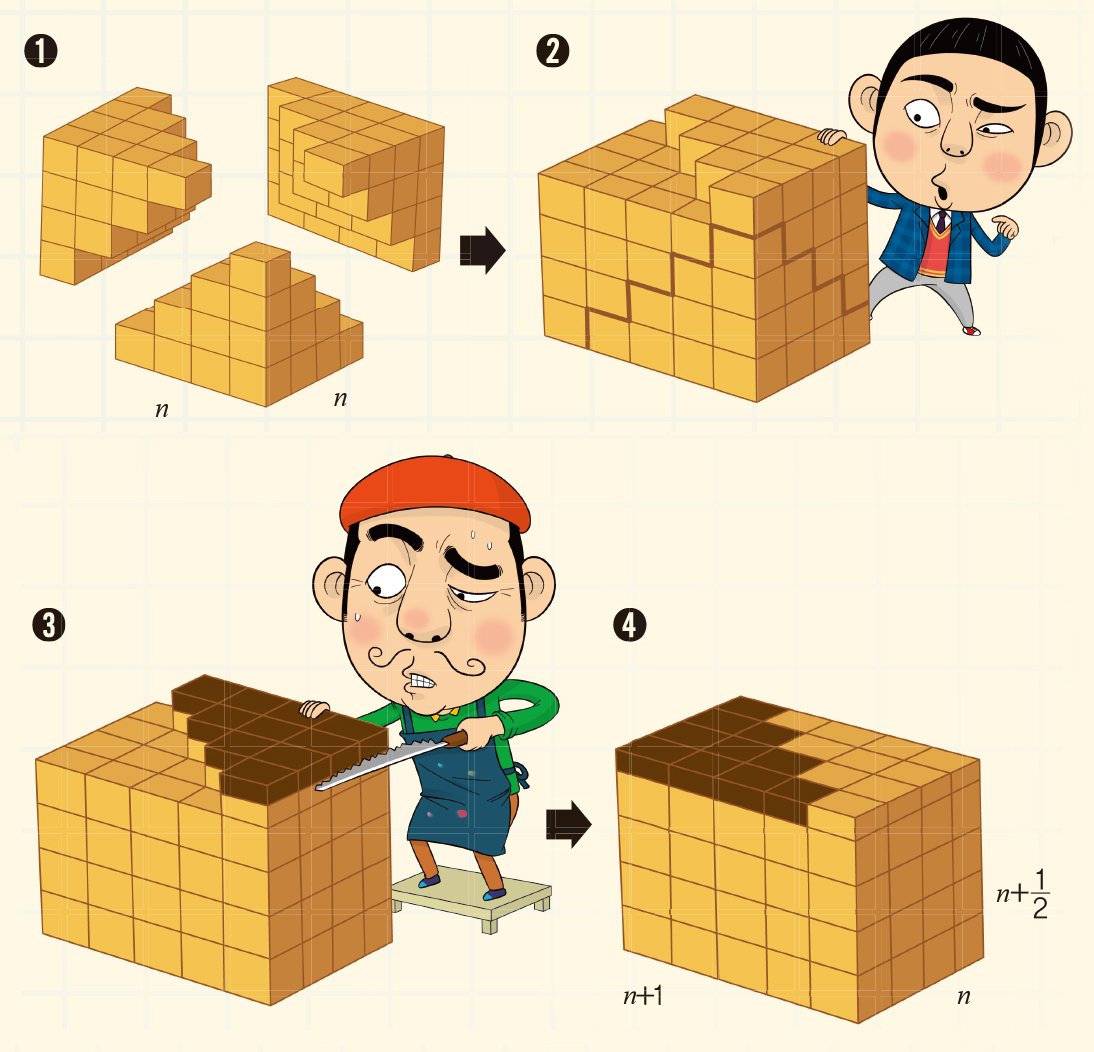
홀수의 합뿐만 아니라, 자연수의 제곱의 합을 구하는 것도 그림 한 장이면 충분하다. 위의 그림은 중국의 수학자 만 긍 쉬우의 그림이다. 그림➊과 같이 피라미드와 비슷한 모양의 쌓기 나무는 n²의 합을 뜻한다. n²의 합에 해당하는 쌓기 나무 3개를 합치면 직육면체와 비슷하지만, 윗부분이 매끄럽지 않은 입체 도형이 된다(그림➋).

이 도형을 직육면체가 되도록 하려면 윗부분에 튀어나온 입체를 반으로 잘라(그림➌) 나머지 오목한 부분에 넣어 그림➍와 같이 만들면 된다. 이 직육면체는 가로, 세로, 높이가 각각 n, n+1, n+(1/2)이므로 직육면체의 부피는 n(n+1)(n+(1/2))이다. 따라서 자연수의 제곱의 합은 (1/3)n(n+1)(n+(1/2))임을 알 수 있다.

수학동아