그림으로 보는 수학 공식 ① 피타고라스의 정리

복잡한 수학 공식도 그림으로 이해하면 머리에 쏙쏙 들어온다. 수학 공식을 알려주는 그림과 그에 얽힌 이야기를 소개한다!

고대 중국의 수학자부터 미국의 대통령까지!

고대 그리스의 수학자 피타고라스는 기원전 500년 경의 사람으로 추정되고 있다. 그런데 서양에서 발견됐다고 알려진 피타고라스의 정리 증명이 기원전 1000년으로 추정되는 고대 중국의 한 수학책에서 이미 소개되었다면 믿을 수 있을까?

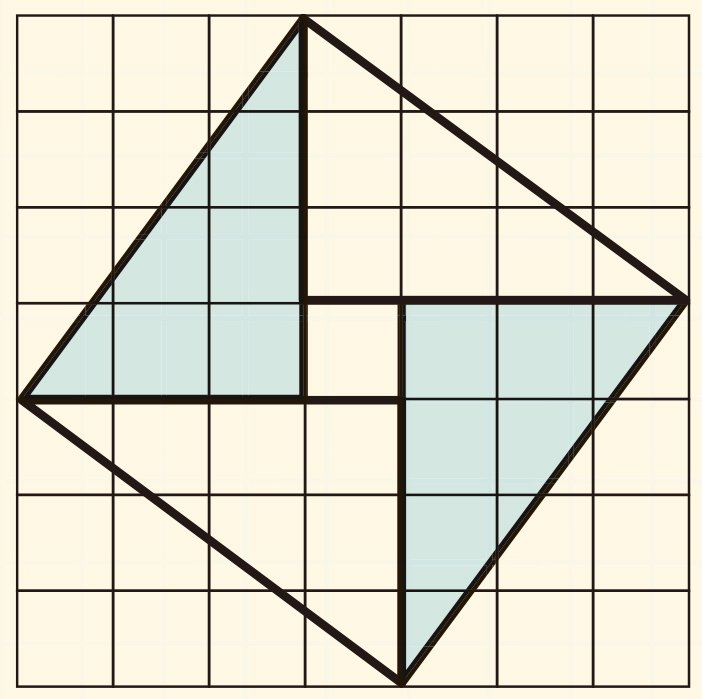
실제로 중국의 고전 수학책으로 가장 오래된 책 중 하나인 ‘주비산경’에는 ‘구고현의 정리’란 이름으로 아래쪽과 같은 한 장의 그림이 소개돼 있다. 정사각형 내부에 작은 정사각형이 내접해 있는 이 그림을 유심히 살펴보자. 빗변을 제외한 한 변의 길이가 3과 4인 직각삼각형을 찾을 수 있다. 그리고 이 직각삼각형의 빗변은 내부에 있는 정사각형의 한 변의 길이기도 하다.

주비산경에 소개된 그림(작자 미상).

그렇다면 내부에 있는 작은 정사각형의 넓이는 얼마일까?

정사각형의 넓이는 한 변의 길이가 3과 4인 직각삼각형 4개와, 한 변의 길이가 1인 정사각형 1개의 넓이의 합으로 나타낼 수 있다. 즉 (3×4)×1/2×4+1=25=5²가 되어, 피타고라스의 정리인 3²+4²=5²를 만족한다. 직관을 중요하게 여긴 이름 모를 동양의 수학자는 어떠한 수식이 없이 한 장의 그림으로 완벽하게 피타고라스의 정리를 표현한 것이다.

헨리 페리갈의 저서 표지.

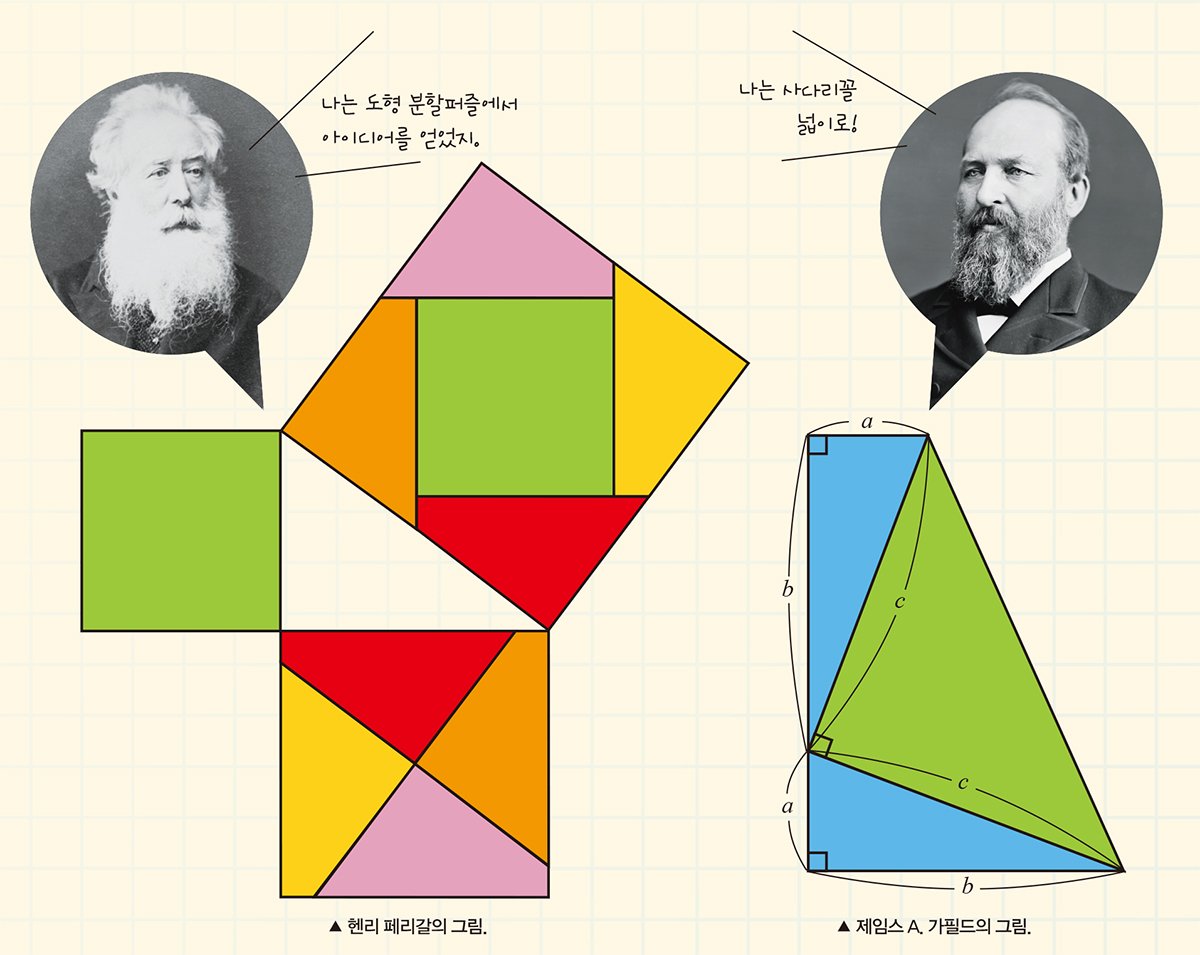
피타고라스의 정리를 쉽게 이해할 수 있는 두 번째 그림은 영국의 증권 중개인이자 아마추어 수학자인 헨리 페리갈의 작품이다. 페리갈은 두 개의 작은 정사각형을 이루는 퍼즐 조각 5개로 큰 정사각형을 만들었다. 피타고라스의 정리를 정사각형의 넓이로 생각해 도형 퍼즐과 같이 표현한 것이다.

이 그림은 영국의 퍼즐왕 헨리 듀드니의 작품으로 알려져 있기도 한데, 페리갈의 작품으로 보는 것이 옳다. 도형 분할로 유명한 퍼즐가 그렉 프레데릭슨의 책에 따르면 페리갈이 이 그림을 발표한 것은 1873년, 듀드니는 1917년이기 때문이다. 그림의 주인으로 혼동되는 두 사람의 이름이 공교롭게도 헨리로 똑같다는 점도 묘한 일이다.

세 번째 작품의 주인은 놀랍게도 대통령이다. 미국의 제 20대 대통령인 제임스 A. 가필드는 위의 오른쪽 그림과 같이 사다리꼴 안에 직각삼각형이 그려진 그림을 그렸는데, 사다리꼴의 넓이를 구하는 과정을 통해 피타고라스의 정리를 쉽게 이해할 수 있다.

사다리꼴의 윗변과 밑변의 길이를 각각 a, b라고 하고, 사다리꼴 내부에 있는 직각이등변삼각형의 한 변의 길이를 c라고 하자. 사다리꼴의 넓이는 (윗변+아랫변)×높이÷2인데, 이는(직각이등변삼각형의 넓이)+2×(나머지 직각삼각형의 넓이)와 같다. 따라서 식으로 나타내면 S=1/2(a+b)² = 2 ×1/2ab+ 1/2c²이므로, 정리하면 c²=a²+b²가 된다.

수학동아