철교는 폭이 넓은 강, 심지어는 바다도 건널 수 있도록 해 준다. 기차나 대형버스가 다녀도 무너지지 않는 이유는 철교가 삼각형으로 이뤄진 ‘트러스’로 이뤄져 있기 때문이다. 높은 빌딩을 세울 때도 쓰이는 이 트러스는 피타고라스 정리를 이용해 간단히 만들 수 있다.
영종대교를 지탱하는 힘!
과거에는 배를 타지 않고 육지에서 섬으로 갈 수 있으리라고 상상도 못 했다. 하지만 이제는 출렁이는 배를 타고 멀미할 걱정이 없다. 육지와 섬을 잇는 다리가 있기 때문이다. 우리는 자동차나 기차를 타고 그 위를 쌩쌩 달릴 수 있다. 사람들은 어떻게 바다 위에 다리를 놓을 수 있었을까?
인천의 육지와 바다 위의 영종도를 잇는 영종대교는 길이 4420m, 너비 41m에 이르는 대형 다리다. 연간 수천만 명이 이 다리를 건너 인천국제공항을 오간다. 영종대교는 상부에 6차선 도로, 하부에 2차선 도로 2개와 철도로 총 2층으로 구성돼 있다.
인천의 육지와 바다 위의 영종도를 잇는 영종대교는 길이 4420m, 너비 41m에 이르는 대형 다리다. 연간 수천만 명이 이 다리를 건너 인천국제공항을 오간다. 영종대교는 상부에 6차선 도로, 하부에 2차선 도로 2개와 철도로 총 2층으로 구성돼 있다.
영종대교는 길이 4420m의 자정식 현수교다. 사진/ⓒmageba
2000년 11월에 완공한 영종대교는 콘크리트의 도움 없이 스스로 모든 하중을 버텨내는 ‘자정식’으로, 3차원 자정식 현수교로는 세계 최초다.
현수교는 다리를 받치는 기둥인 ‘교각’ 외에 케이블을 이용해 다리 양쪽을 당기는 방식으로 지지하는 다리를 말한다.
하지만 케이블만으로 무려 4km가 넘는 긴 다리를 지탱할 수는 없다. 영종대교를 지탱하는 진짜 힘은 바로 ‘트러스’다. 트러스란 직선으로 된 여러 개의 뼈대 재료를 삼각형 모양으로 이은 구조를 말한다. 세 직선이 모인 삼각형으로 이뤄진 영종대교의 트러스는 다리의 무게를 여러 군데로 분산시킨다. 덕분에 케이블에 들어가는 힘은 줄면서 현수교는 더욱 안정하고 튼튼해진다.
하지만 케이블만으로 무려 4km가 넘는 긴 다리를 지탱할 수는 없다. 영종대교를 지탱하는 진짜 힘은 바로 ‘트러스’다. 트러스란 직선으로 된 여러 개의 뼈대 재료를 삼각형 모양으로 이은 구조를 말한다. 세 직선이 모인 삼각형으로 이뤄진 영종대교의 트러스는 다리의 무게를 여러 군데로 분산시킨다. 덕분에 케이블에 들어가는 힘은 줄면서 현수교는 더욱 안정하고 튼튼해진다.
트러스는 왜 삼각형으로 이뤄져 있을까? 그것은 삼각형이 사각형 같은 다른 도형보다 훨씬 안정적이기 때문이다.
사각형은 좌우로 미는 힘이나 위아래로 누르는 힘에 금세 모양이 변형되기 쉬운 반면에 삼각형은 외부에서 힘을 받아도 모양이 잘 흐트러지지 않는다. 대각선의 뼈대 재료가 한 번 더 구조를 안정적으로 받쳐 주기 때문이다. 그렇다면 이런 트러스는 어떻게 만들까?
수많은 삼각형으로 이뤄진 트러스교. 사진/Hugues(f)
대각선 뼈대의 길이 구하기
트러스로 튼튼한 다리를 직접 설계해 보자. 먼저 교각의 개수를 결정해야 한다. 교각을 촘촘히 설치하면 더 튼튼하고 안전한 다리가 된다. 그러나 비용도 많이 들고 오래 걸리기 때문에 무조건 교각을 많이 설치할 수는 없다. 무엇보다 다리 밑 공간을 효과적으로 활용할 수 없다. 교각이 너무 촘촘하면 교각 사이로 또 다른 도로를 놓거나 강이나 바다 위에서 배가 지나다닐 수 없기 때문이다.
그래서 교각과 교각 사이는 다리 상판에 작용하는 하중을 교각으로 충분히 전달할 수 있는 최대의 거리만큼 띤다. 그 다음이 트러스다. 교각의 수를 최소로 하려면, 트러스가 튼튼해야 한다. 삼각형이 많을수록 튼튼하겠지만, 트러스 자체의 무게가 너무 무거워지거나 비용이 너무 많이 들면 비효율적이다. 그래서 적당한 크기의 삼각형으로 구성해야 한다.
그래서 교각과 교각 사이는 다리 상판에 작용하는 하중을 교각으로 충분히 전달할 수 있는 최대의 거리만큼 띤다. 그 다음이 트러스다. 교각의 수를 최소로 하려면, 트러스가 튼튼해야 한다. 삼각형이 많을수록 튼튼하겠지만, 트러스 자체의 무게가 너무 무거워지거나 비용이 너무 많이 들면 비효율적이다. 그래서 적당한 크기의 삼각형으로 구성해야 한다.
트러스 자체가 무거우면 비효율적이기 때문에 삼각형 크기를 적당히 조절해야 한다. 사진/Nv8200pa(w)
삼각형의 크기를 결정하는 방법 중 하나는 두 변의 길이와 그 사잇각을 정하는 것이다. 그러면 나머지 한 변은 두 변의 끝을 잇는 선분이 된다.
트러스를 이루는 직각삼각형에서는 밑변과 높이를 정하면, 빗변이 자동으로 결정된다. 이때 피타고라스 정리를 이용하면, 이 빗변의 길이를 구할 수 있다.
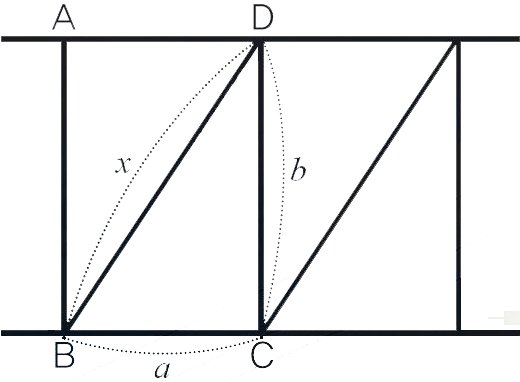
피타고라스 정리는 직각삼각형에서 빗변이 아닌 두 변의 길이를 각각 제곱해 더하면 빗변의 길이를 제곱한 값이 된다는 것이다. 오른쪽 그림과 같은 트러스의 가로, 세로의 길이가 각각 a, b인 직사각형 ABCD에서 직각삼각형 BCD의 빗변 BD의 길이를 x라고 하면 피타고라스 정리에 의해 x2=a2+b2이다. 그런데 x는 변의 길이로 x>0이므로, x=√(a2+b2)가 된다.
밑변 BC의 길이 a가 3m, 높이 CD의 길이 b가 4m가 되도록 하려면, 빗변 BD의 길이 x는 몇 m가 돼야 할까? 피타고라스 정리에 따라 x2=32+42이므로, x2=25임을 알 수 있다. 이때 x= √25=√52=5이므로, 트러스를 만들려면 대각선 뼈대는 5m가 돼야 한다.
수학동아
댓글 없음:
댓글 쓰기