동양과 서양의 방정식 ③ 천원술과 산대로 푸는 동양의 방정식

17세기 비슷한 시기를 산 동·서양의 두 수학자 데카르트와 홍정하. 두 사람은 모두 방정식에 일가견이 있는 수학자들이다. 데카르트는 오늘날 전세계 사람들이 쓰고 있는 문자 를 처음 도입했고, 조선 최고의 수학자로 손꼽히는 홍정하는 자신의 저서 <구일집>에 방정식의 산대 표기를 처음으로 쓴 수학자다. 그러나 오늘날, 우리가 접하고 있는 방정식은 모두 서양의 수학을 따르고 있다. 방정식은 정말 서양에만 있었던 걸까?

‘천원술’과 ‘산대’만 있으면 방정식 OK!

아라비아 숫자와 문자가 없던 동양에서도 방정식을 풀 수 있었을까?

결론부터 말하면 우리나라를 포함한 동양에도 방정식이 있었고, 방정식을 풀 수 있었다.
동양에서는 방정식을 ‘천원술’이라는 방법을 통해 표현했다. 천원술에서 ‘천원’은 미지수, 오늘날로 말하면 x를 뜻한다. 방정식 표기는 계산할 때 쓰는 도구인 나무 막대 ‘산대’를 이용했다. 천원술에서는 미지수의 거듭제곱을 기호나 문자로 쓰지 않고, 정해진 자리에 계수만 세로로 나열했다.

예를 들어 오늘날 문자로 나타낸 방정식 -7x³+243x²+2187x+6561=0을 천원술로 나타내면 왼쪽 아래 그림과 같다. (단, 계수가 음수일 때에는 산대에 대각선 막대를 덧붙여 표기한다.) 그렇다면 방정식은 어떻게 풀 수 있었을까? 홍정하의 저서 <구일집> 제4권에 나오는 간단한 문제와 풀이를 살펴보자.

이러한 풀이 방법은 오늘날 각 미지수에 문자를 두고, 계수를 소거해 연립방정식을 푸는 ‘가우스-요르단 소거법’과 그 원리가 같다. 다만 동양에서는 문자를 쓰지 않고 계수만 쓴다는 점이 다를 뿐이다.

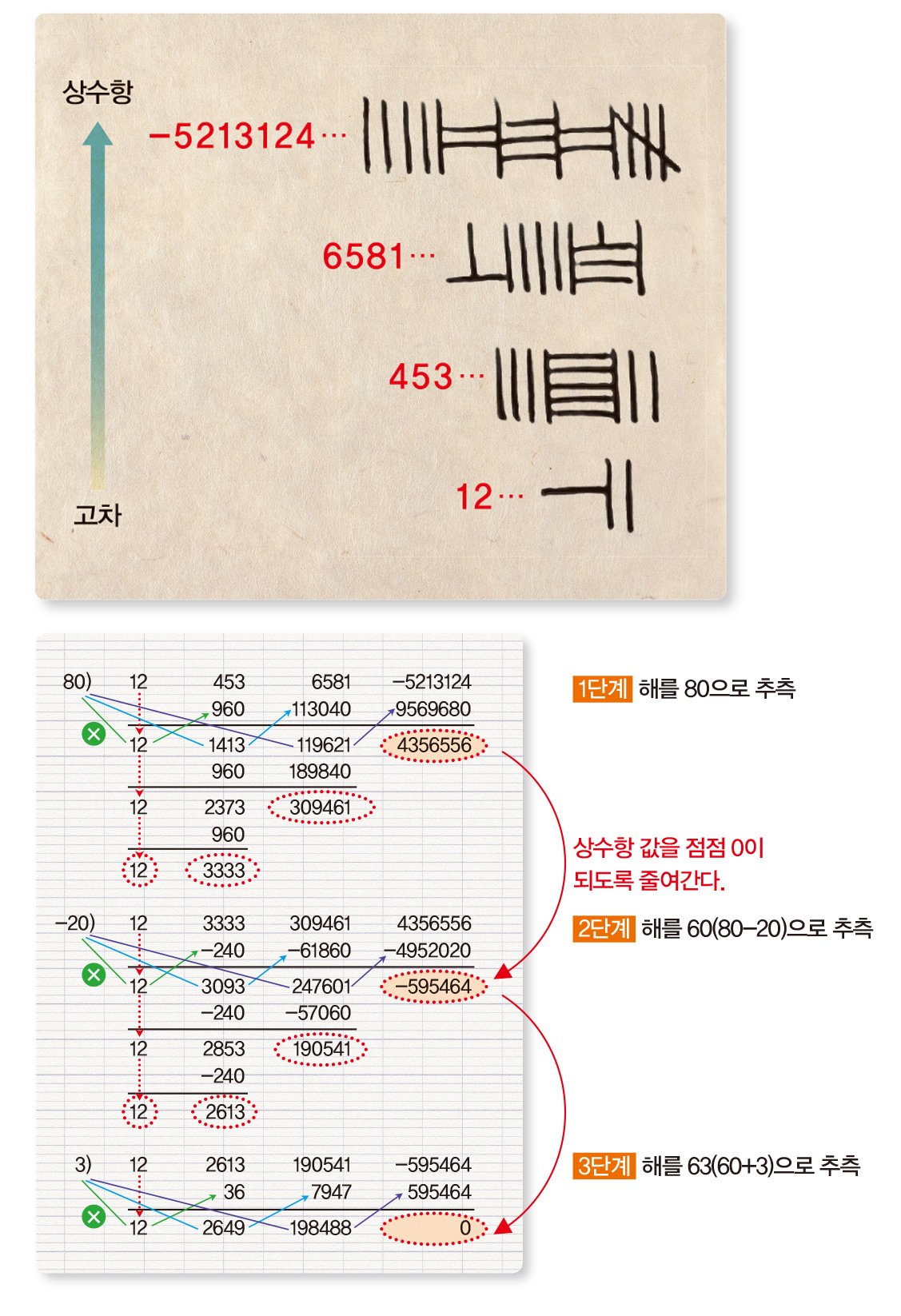
고차방정식 문제 하나를 더 살펴보자. 왼쪽 아래와 같이 산대로 표기한 방정식은 간단해 보이지만, 이 식을 문자로 나타내면 12x³+453x²+6581x-5213124=0이란 계수가 복잡한 3차 방정식이다. 자연수 해는 63인데, 풀이 방법은 아래와 같다.

해를 구하는 방법은 처음에 대략 해가 될 것 같은 수를 추측해 상수항의 값을 본 다음, 적절하게 더하고 빼는 과정을 반복하는 것이다. 오늘날의 고차방정식의 정수해를 구할 때 쓰는 ‘조립제법’과 비슷하다. 이 방법은 19세기 영국의 수학자 호너가 제안한 방법과도 같다. 동양에서는 서양보다 300년이나 앞서 이 방법을 알고 있었던 셈이다.

그런데 사실 동양에서 이런 방법으로 해를 구한 데에는 나름의 이유가 있다. 동양의 방정식은 대부분 실생활 문제와 관련이 있어서 위와 같이 복잡한 계수의 방정식이 많았다. 이 때문에 무리수나복소수와 같은 해나, 일반적인 해를 구하는 방법보다는 근사해를 구하는 것에 더 관심을 두었던 것이다.

지금까지 살펴보았듯이 서양과 동양의 방정식은 당시 상황과 문화를 토대로 방정식을 바라본 관점도 모양도 조금씩 다르다. 그러나 오랜 시간 동안 방정식을 풀고자 했던 수학자들의 열정만은 동, 서양에 관계없이 같지 않았을까.

수학동아