우리가 알고 있는 구구단이 곱셈법의 전부는 아니다. 과거 조상들은 저마다 독특한 곱셈법을 개발해서 사용했다. 어떤 것들이 있는지 알아보자!
선만 잘 그으면 곱셈이 된다?!
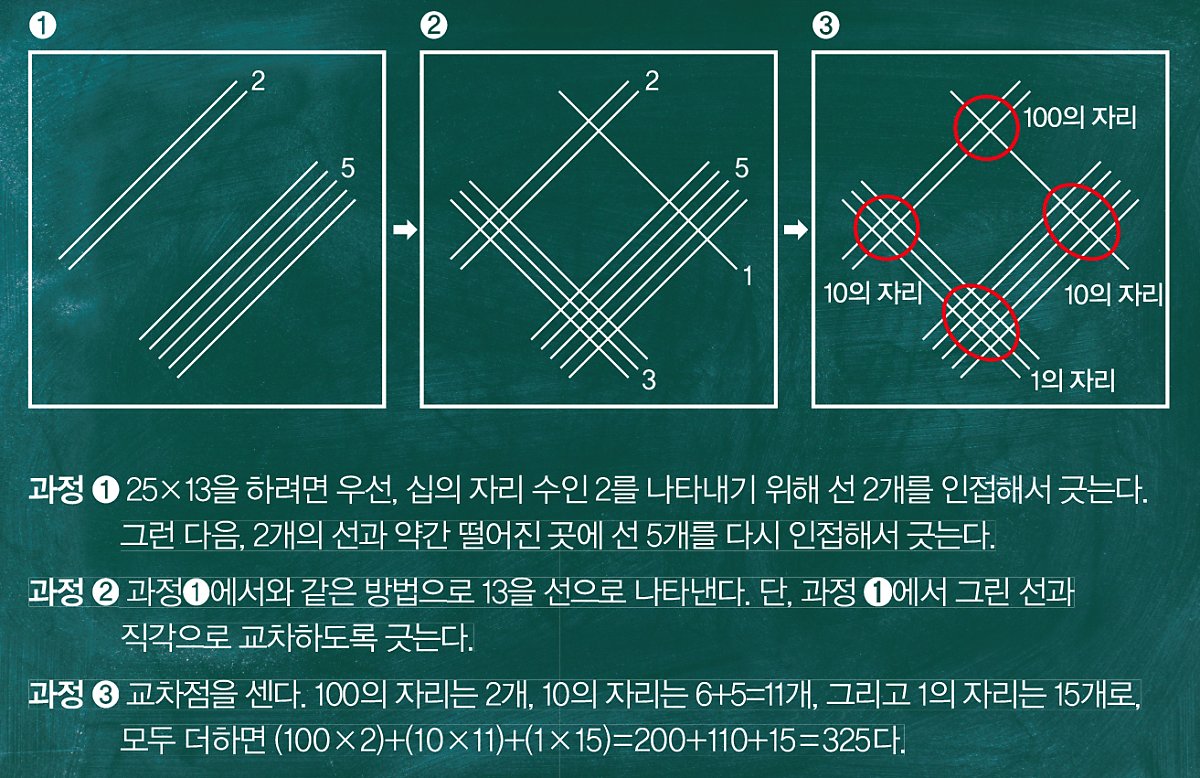
선 긋기 곱셈법은 자연수의 곱셈 원리를 잘 활용한 방법이다.
자연수의 곱셈은 덧셈으로 바꿔 나타낼 수 있다. 예를 들어 3 곱하기 5는 3을 5번 더하면 된다. 선긋기에서 교차점의 개수는 자연수를 연속으로 더한 값이 된다.
예를 들어 아래 그림과 같이 그은 선에서 교차점은 3+3(또는 2+2+2)으로, 3×2를 나타낸다. 따라서 교차점이 의미하는 자릿수만 알면, 교차점의 개수를 묶은 다음 더하는 것으로 곱셈 값을 쉽게 구할 수 있다.
겔로시아 곱셈법과 존 네이피어의 계산막대
표를 사용해 곱셈을 하는 방법에는 겔로시아 곱셈법과, 존 네이피어의 계산막대를 사용한 곱셈법이 있다. 먼저 겔로시아 곱셈법의 ‘겔로시아’는 ‘격자’를 뜻하는 말로, 이 곱셈법은 인도에서 처음 시작된 것으로 추정되고 있다.
인도의 수학자 바스카라가 지은 수학책인 <릴라바티>에 등장했고, 또 다른 인도의 수학책에서도 겔로시아 곱셈법이 나타나 있기 때문이다. 겔로시아 곱셈법은 현재 많은 사람들이 사용하는 세로 곱셈법과 원리가 같으며, 사선으로 배열해 수를 더하는 방식이다.
반면 네이피어의 곱셈법은 구구단을 막대로 만들어 곱셈을 쉽게 하도록 만든 것이다. 구구단 계산막대가 있기 때문에 당연히 구구단을 외울 필요가 없지만, 항상 계산막대가 있어야 한다. 네이피어는 계산의 혁명이라고 부르는 ‘로그(log)’를 발명한 수학자로도 잘 알려져 있다.
수학동아



댓글 없음:
댓글 쓰기