수리논리학에서, 괴델의 불완전성 정리(영어: Gödel’s incompleteness theorems)는 페아노 공리계를 포함하는 모든 무모순적 공리계는 참인 일부 명제를 증명할 수 없으며, 특히 스스로의 무모순성을 증명할 수 없다는 정리다.
19세기에 카를 프리드리히 가우스, 보여이 야노시, 니콜라이 로바쳅스키, 베른하르트 리만 등의 연구를 통해서, 유클리드 기하학의 다른 공준으로부터 평행선 공준을 유도하는 것은 불가능하다는 사실이 증명되었다.[1] 유클리드 공리체계의 1번~4번 공준을 그대로 사용하면서 5번 공준의 부정을 택한 비유클리드 기하학이 유클리드 기하학과 동등하게 성립했던 것이다. 비유클리드 기하학의 성장으로 인해 사람들은 주어진 체계 내에서 어떤 명제의 증명 불가능을 증명할 수 있다는 메타-증명에 관심을 갖기 시작했다. 괴델의 논문도 산술학에서 몇 가지 중요한 명제의 증명 불가능을 증명한 것이다. 또한 기하학의 공리가 자명성을 가지는 전통적인 믿음이 흔들리게 되면서 수학의 목표는 실제 세계의 표상이라기보다는 공준화된 최초의 가정에서 결론을 필연적으로 도출할 수 있는지를 따지는 추상적이고 형식적인 학문으로 인식되게 되었다. 이렇게 수학이 직관과 상식을 벗어나 형식화, 추상화되면서, 체계의 근거로 사용되는 공준의 집합체가 내적으로 모순되지 않고, 따라서 "공준에서 서로 모순되는 정리가 추론되는 경우는 없는가"라는 무모순성의 문제가 제기되었다. 형식적인 수학에서는 '진리'와 '증명가능성'의 개념이 구별되어 쓰인다. 즉, 한 공리 체계에서 연역적으로 어떤 정리를 도출할 수 있으면 그 정리는 증명가능한 것인데, 그 체계 내에서 거짓임을 증명할 수 없는 어떤 진술이 항상 참임을 증명할 수 있다는 보장은 없는 것이다.
논리학에서 무모순성은 의미론적 또는 구문론적으로 정의될 수 있다. 의미론적인 정의는 어떤 이론이 모형을 가질 때 무모순이라는 것이며, 구문론적인 정의는 그 연역체계의 공리로부터 공식 P와 공식의 부정 ~P가 동시에 증명 가능한 P가 존재하지 않을 때 무모순이라는 것이다.
어떤 체계의 추상적 공준들을 위한 모형을 찾아낸다면 무모순성을 해결할 수 있다. 모형에 포함된 모든 원소가 공준을 실제로 만족시키는지, 그리고 모든 공준이 참값이어서 서로 모순되지 않는지 실제의 관찰을 통해 판별하는 것이다. 유클리드 기하학의 경우 모형은 일상적 공간이다. 유클리드의 공리는 일상적 공간에서 언제나 참값이며, 따라서 서로 모순되지 않는다. 리만 평면 기하학의 무모순성도 유클리드 기하학 모형을 사용함으로써 입증할 수 있다. 리만의 공리에서 ‘평면’이란 용어는 유클리드 구면의 표면을, ‘점’이란 용어는 그 표면 위의 한쌍의 대척점을, ‘직선’이란 용어는 그 표면 위의 대원의 호를 의미하는 것으로 해석할 수 있고 리만 기하학의 정리들은 모두 유클리드의 정리로 변환될 수 있다. 그러나 이러한 상대적인 무모순성의 해결은 여기서 가정한 유클리드 체계의 공리들이 서로 모순되지 않는다는 보장이 필요한데, 무모순성의 해결 기준이 엄격해짐에 따라 유클리드 기하학의 모형이 되는 ‘일상적인 공간’ 에 대한 실제 경험 또한 절대적 무모순성을 보장해주지 못하게 되었다. 관찰된 모든 현상이 공리와 일치하더라도, 지금까지 관찰되지 않은 새로운 현상이 공리에 모순될 가능성이 있기 때문이다. 귀납적 증거는 공리가 타당성 있고 참값일 가능성이 크다고 말할 수 있을 뿐이다.
다비트 힐베르트는 유클리드의 공준을 데카르트 해석기하학의 대수적 참값으로 변환함으로써 유클리드 공준이 대수적 모형로 만족됨을 증명하였지만, 이는 여전히 다른 체계의 무모순성을 근거로 한 상대적 증명에 해당한다. 대수에 모순이 없다면 유클리드 기하학의 무모순성이 입증될 수 있을 것이므로, 산술체계의 무모순성을 확립하는 문제가 중요해진다.
다비트 힐베르트는 한 쪽 끝에 어떤 진술을 집어넣든지 간에, 크랭크를 돌리고 뒤로 물러앉아 있기만 하면 다른 쪽 끝에서 참/거짓이라는 대답이 나오는 진리기계(형식화된 공식체계)를 구상했다. 이는 수학을 형식화된 공식체계로 한 다음 그 체계의 무모순성을 ‘유한한 초수학적 방법’으로 증명함으로써 가능하다. 모든 산술적 진술의 참과 거짓을 결정할 수 있게 해주는 어떤 유한한 기계적 절차가 존재하느냐 하는 힐베르트의 결정문제에 대해, 형식화의 방법은 무한하게 많을 것이다. 괴델의 정리에 따르면 힐베르트 연구 계획의 모든 요구조건을 만족시키는 형식체계는 무한한 형식화의 모든 경우에 대해 존재하지도 않으며, 존재할 수도 없다.
힐베르트는 연역적인 체계를 형식화하려고 했다. 여기서 "형식화"란 체계 내의 표현식들의 '의미'를 제거하고 기호들의 연쇄체로 표시하는 것이다. 이 작업을 위해 힐베르트는 "수학"과 "초수학"을 구분했다. "초수학적 진술"이란, 메타 수학, 즉, 수학에 대한, 수학을 설명하는 언어에 속하는 것이다. 체계 안에서 사용된 부호에 대한 진술일 수도 있고, 체계 그 자체에 대한 진술일 수도 있다. 예를 들어 "1+1=2"는 수학에 속하는 것이지만, "'1+1=2'는 산술 공식이다."는 초수학에 속한다. "산술에 대한 이론 체계가 무모순이다." 또는 괴델의 불완전성 정리의 함축 같은 것도 모두 초수학에 속하는 것들이다.
 이 부분의 본문은 수학 원리입니다.
러셀의 역설 등에서의 역설적인 요소는 그 역설의 진술이 지닌 의미론적인 내용에 기인한다고 믿었던 힐베르트는 본질적으로 무의미한 형식 체계를 정의하였고, 그 안에서 수학적 진술들의 참 또는 거짓에 대해 말하고자 했다. 공준과 공리를 비롯한 모든 식은 의미 없는 부호 체계, 형식화된 표시들의 기호열로 여겨진다. 공준에서 정리를 유도하는 것은 어떤 기호열의 집합을 다른 기호열의 집합으로 전환하는 것이다. 이렇게 형식화는 체계의 모든 정리들을 공리로부터 유도될 수 있도록 부호 체계를 구축하는 것이고, 여기서 모순되는 두 공식은 정해진 추론 법칙으로 공리에서 동시에 유도될 수 없음을 보이면 무모순성이 증명된다.
이 부분의 본문은 수학 원리입니다.
러셀의 역설 등에서의 역설적인 요소는 그 역설의 진술이 지닌 의미론적인 내용에 기인한다고 믿었던 힐베르트는 본질적으로 무의미한 형식 체계를 정의하였고, 그 안에서 수학적 진술들의 참 또는 거짓에 대해 말하고자 했다. 공준과 공리를 비롯한 모든 식은 의미 없는 부호 체계, 형식화된 표시들의 기호열로 여겨진다. 공준에서 정리를 유도하는 것은 어떤 기호열의 집합을 다른 기호열의 집합으로 전환하는 것이다. 이렇게 형식화는 체계의 모든 정리들을 공리로부터 유도될 수 있도록 부호 체계를 구축하는 것이고, 여기서 모순되는 두 공식은 정해진 추론 법칙으로 공리에서 동시에 유도될 수 없음을 보이면 무모순성이 증명된다.
형식화의 과정은 다음과 같다.
유클리드 기하학 뿐만 아니라 일반적인 수학 체계는 주세페 페아노 등에 의해 산술화되었고, 고틀로프 프레게, 버트런드 러셀 등 논리주의자들에 의해 산술체계가 논리학 명제로 표현될 수 있었다. 따라서 수학의 무모순성 문제는 형식논리학 자체의 무모순성 문제로 귀결되었고, 논리주의 진영의 앨프리드 노스 화이트헤드와 버트런드 러셀이 《수학 원리》에서 순수 수학(산술)의 모든 진술을 형식화하는 방법을 제공하였다. 《수학 원리》에 제시된 포괄적인 표기 체계에 따라 순수 수학에 속하는 모든 명제를 표준적인 방법에 맞추어 코드할 수 있다.
이 정리는 수학의 체계를 완전하고 모순이 없는 공리계로 형식화하려는 힐베르트의 계획의 실패를 알리는 것으로 인식된다. 보다 구체적으로는, 이는 힐베르트의 두 번째 문제에 대한 부정적인 해답으로 볼 수도 있다.
 은 다음 네 성질들을 동시에 만족시킬 수 없다.
은 다음 네 성질들을 동시에 만족시킬 수 없다.
 은 부호수
은 부호수 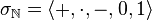 의 1차 논리 구조를 이룬다. 이 경우,
의 1차 논리 구조를 이룬다. 이 경우,  에서 참인 1차 논리
에서 참인 1차 논리  -명제들의 집합
-명제들의 집합  은 재귀 열거 집합이 아니다. (1차 논리의 경우, 괴델의 완전성 정리에 의하여 모형 이론적인 진리는 증명 이론적 진리와 일치한다.)
은 재귀 열거 집합이 아니다. (1차 논리의 경우, 괴델의 완전성 정리에 의하여 모형 이론적인 진리는 증명 이론적 진리와 일치한다.)
마찬가지로, 이를 2차 논리의 증명 이론으로도 서술할 수 있다. 2차 논리에서는 페아노 공리계가 자연수 체계의 완전한 공리화를 이룬다. (즉, 페아노 공리계의 표준 모형(영어: standard model)은 자연수 집합밖에 없다.) 이 경우, 괴델의 제1 불완전성 정리에 따르면 페아노 공리의 2차 논리 체계는 (2차 논리의 표준 모형에서) 괴델 완전성 정리를 만족시키지 못한다. 즉, 2차 논리의 임의의 재귀 열거 가능 증명 이론에 대하여, 항상 페아노 공리로부터 증명할 수 없지만 참인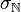 -명제가 존재한다. (물론, 2차 논리에서 헹킨 모형(영어: Henkin model)을 사용하면 적절한 증명 이론이 존재하지만, 헹킨 모형을 부여한 2차 논리는 사실상 1차 논리와 같으므로 이 경우 페아노 공리로부터 증명할 수 없지만 자연수에 대하여 참인 명제가 존재한다.)
-명제가 존재한다. (물론, 2차 논리에서 헹킨 모형(영어: Henkin model)을 사용하면 적절한 증명 이론이 존재하지만, 헹킨 모형을 부여한 2차 논리는 사실상 1차 논리와 같으므로 이 경우 페아노 공리로부터 증명할 수 없지만 자연수에 대하여 참인 명제가 존재한다.)
 은 다음 다섯 성질들을 동시에 만족시킬 수 없다.
은 다음 다섯 성질들을 동시에 만족시킬 수 없다.
 의 명제들은 가산 무한 알파벳
의 명제들은 가산 무한 알파벳  로 기술된다고 하자. 예를 들어, 체르멜로-프렝켈 집합론의 경우 논리적 기호
로 기술된다고 하자. 예를 들어, 체르멜로-프렝켈 집합론의 경우 논리적 기호 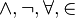 및 변수
및 변수 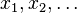 의 집합으로 삼을 수 있다. 즉, 모든 명제들은
의 집합으로 삼을 수 있다. 즉, 모든 명제들은  의 클레이니 스타
의 클레이니 스타 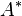 의 원소이다. (물론
의 원소이다. (물론 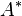 는 문법에 맞지 않는 기호열들을 포함하므로, 명제의 집합은
는 문법에 맞지 않는 기호열들을 포함하므로, 명제의 집합은 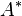 의 부분집합이다.) 그렇다면 명제의 괴델 수(영어: Gödel number)
의 부분집합이다.) 그렇다면 명제의 괴델 수(영어: Gödel number)
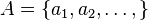 라고 하고,
라고 하고,  번째 소수를
번째 소수를 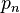 이라고 하면,
이라고 하면,
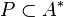 가
가  에서 증명 가능한 명제들의 집합이라고 하자. 그렇다면 그 상
에서 증명 가능한 명제들의 집합이라고 하자. 그렇다면 그 상 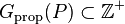 은 양의 정수의 부분집합이다.
은 양의 정수의 부분집합이다.
또한, 가 유효 생성 이론이라고 가정하였으므로, 모든 가능한 증명 또한 괴델 수를 부여할 수 있다. 즉, 증명의 집합을
가 유효 생성 이론이라고 가정하였으므로, 모든 가능한 증명 또한 괴델 수를 부여할 수 있다. 즉, 증명의 집합을 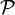 라고 한다면,
라고 한다면,  가 존재한다.
가 존재한다.
페아노 공리계만을 사용하여, 다음과 같은 이항 관계 를 정의하자.
를 정의하자.  는 다음을 의미한다.
는 다음을 의미한다.
 를 갖는 명제를 생각할 수 있다.
를 갖는 명제를 생각할 수 있다.
 가 이 명제를 증명할 수 있다면,
가 이 명제를 증명할 수 있다면,  는 모순적이다.
는 모순적이다.
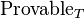 는
는  에서 증명할 수 있다는 뜻이다.
에서 증명할 수 있다는 뜻이다.
 속의 한 명제로 나타낼 수 있다. 이 명제를
속의 한 명제로 나타낼 수 있다. 이 명제를 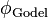 라고 쓰자. 또한,
라고 쓰자. 또한,  속에서
속에서  스스로가 무모순적이라는 명제를
스스로가 무모순적이라는 명제를 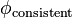 라고 쓰자. 그렇다면
라고 쓰자. 그렇다면
정의에 따라서 다음과 같은 동치가 성립한다.
 속에서 증명할 수 있다. 제1 불가능성 정리의 증명을
속에서 증명할 수 있다. 제1 불가능성 정리의 증명을  속에서 재현하여, 함의
속에서 재현하여, 함의
 속에서 증명할 수 있다. 따라서, 만약
속에서 증명할 수 있다. 따라서, 만약  속에서
속에서 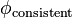 를 증명할 수 있다면
를 증명할 수 있다면  을
을  속에서 증명할 수 있다. 그러나 이는 제1 불완전성 정리에 의하여
속에서 증명할 수 있다. 그러나 이는 제1 불완전성 정리에 의하여  속에서 증명할 수 없다. 이는 모순이므로,
속에서 증명할 수 없다. 이는 모순이므로,  속에서
속에서 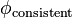 를 증명할 수 없다.
를 증명할 수 없다.
목차
[숨기기]역사와 배경[편집]
무모순성 문제의 제기[편집]
수학은 공리적 방법을 통해 확실성과 엄밀성이 특징인 학문으로 발전해왔다. 수학은 19세기 초에 상식과 동떨어진 새로운 형태의 기하학과 대수학이 출현하면서 스스로의 진리 여부를 검토하게 되었다. 19세기 후반 수학의 엄밀화를 위한 운동이 진행되지만, 새로 구성한 수학에서 역설이 발견되었고 이 모순을 해결하기 위해 수학기초론의 세 가지 접근방식이 발전하였다. 수학적 존재에 대한 인간의 직관에 의해 수학이 도출된다고 하는 직관주의, 수학을 내용이나 의미가 없는 하나의 형식적 조작으로 귀착시키려는 형식주의, 수학의 개념과 정리가 논리학의 공리계에서 연역될 수 있다고 보는 논리주의가 그것이다.19세기에 카를 프리드리히 가우스, 보여이 야노시, 니콜라이 로바쳅스키, 베른하르트 리만 등의 연구를 통해서, 유클리드 기하학의 다른 공준으로부터 평행선 공준을 유도하는 것은 불가능하다는 사실이 증명되었다.[1] 유클리드 공리체계의 1번~4번 공준을 그대로 사용하면서 5번 공준의 부정을 택한 비유클리드 기하학이 유클리드 기하학과 동등하게 성립했던 것이다. 비유클리드 기하학의 성장으로 인해 사람들은 주어진 체계 내에서 어떤 명제의 증명 불가능을 증명할 수 있다는 메타-증명에 관심을 갖기 시작했다. 괴델의 논문도 산술학에서 몇 가지 중요한 명제의 증명 불가능을 증명한 것이다. 또한 기하학의 공리가 자명성을 가지는 전통적인 믿음이 흔들리게 되면서 수학의 목표는 실제 세계의 표상이라기보다는 공준화된 최초의 가정에서 결론을 필연적으로 도출할 수 있는지를 따지는 추상적이고 형식적인 학문으로 인식되게 되었다. 이렇게 수학이 직관과 상식을 벗어나 형식화, 추상화되면서, 체계의 근거로 사용되는 공준의 집합체가 내적으로 모순되지 않고, 따라서 "공준에서 서로 모순되는 정리가 추론되는 경우는 없는가"라는 무모순성의 문제가 제기되었다. 형식적인 수학에서는 '진리'와 '증명가능성'의 개념이 구별되어 쓰인다. 즉, 한 공리 체계에서 연역적으로 어떤 정리를 도출할 수 있으면 그 정리는 증명가능한 것인데, 그 체계 내에서 거짓임을 증명할 수 없는 어떤 진술이 항상 참임을 증명할 수 있다는 보장은 없는 것이다.
논리학에서 무모순성은 의미론적 또는 구문론적으로 정의될 수 있다. 의미론적인 정의는 어떤 이론이 모형을 가질 때 무모순이라는 것이며, 구문론적인 정의는 그 연역체계의 공리로부터 공식 P와 공식의 부정 ~P가 동시에 증명 가능한 P가 존재하지 않을 때 무모순이라는 것이다.
어떤 체계의 추상적 공준들을 위한 모형을 찾아낸다면 무모순성을 해결할 수 있다. 모형에 포함된 모든 원소가 공준을 실제로 만족시키는지, 그리고 모든 공준이 참값이어서 서로 모순되지 않는지 실제의 관찰을 통해 판별하는 것이다. 유클리드 기하학의 경우 모형은 일상적 공간이다. 유클리드의 공리는 일상적 공간에서 언제나 참값이며, 따라서 서로 모순되지 않는다. 리만 평면 기하학의 무모순성도 유클리드 기하학 모형을 사용함으로써 입증할 수 있다. 리만의 공리에서 ‘평면’이란 용어는 유클리드 구면의 표면을, ‘점’이란 용어는 그 표면 위의 한쌍의 대척점을, ‘직선’이란 용어는 그 표면 위의 대원의 호를 의미하는 것으로 해석할 수 있고 리만 기하학의 정리들은 모두 유클리드의 정리로 변환될 수 있다. 그러나 이러한 상대적인 무모순성의 해결은 여기서 가정한 유클리드 체계의 공리들이 서로 모순되지 않는다는 보장이 필요한데, 무모순성의 해결 기준이 엄격해짐에 따라 유클리드 기하학의 모형이 되는 ‘일상적인 공간’ 에 대한 실제 경험 또한 절대적 무모순성을 보장해주지 못하게 되었다. 관찰된 모든 현상이 공리와 일치하더라도, 지금까지 관찰되지 않은 새로운 현상이 공리에 모순될 가능성이 있기 때문이다. 귀납적 증거는 공리가 타당성 있고 참값일 가능성이 크다고 말할 수 있을 뿐이다.
집합론의 발달[편집]
유한 모형은 직접 관찰을 통해 무모순성을 입증할 수 있지만, 수학에서 중요한 분야의 기초를 이루는 공준 체계의 대부분은 무한 모형이다. 가령 “모든 정수는 바로 다음에 오는 정수가 있으며, 그 정수는 앞에서 사용된 어떤 정수와도 다르다”는 초등산술의 공준은 무한수의 원소를 포함한 집합에 속할 것이 요구된다. 그런데 수학적으로 중요한 위치를 차지하는 대부분의 공준 체계를 해석하는 데 필요한 무한 모형은 직관에 의존하는 개략적 용어로 표현될 따름이며, 무한 모형의 표현 자체에 모순이 숨어있을 수 있다. 실제로 19세기 게오르크 칸토어가 발전시킨 기수와 순서수의 이론에서 칸토어 역설 및 부랄리포르티 역설의 발견으로 인하여, 군 혹은 집합과 같이 가장 명백한 것으로 여겨졌던 기초 개념에서 출발한 체계까지도 무모순성을 보장할 수 없었다. 버트런드 러셀은 기초 논리학을 구축하는 과정에서 칸토어의 무한 집합론에서 발견된 모순과 매우 유사한 러셀의 역설을 발견하였다.힐베르트의 연구 프로그램[편집]
형식주의자였던 다비트 힐베르트는 1925년의 논문 〈무한에 관하여〉(독일어: Über das Unendliche)[2] 에서 내용이나 의미가 명확한 수학문제는 언젠가는 반드시 풀릴 것이라고 했고, 이어서 1930년에 출판된 책 《수학의 기초》(독일어: Grundlagen der Mathematik)에서도 초수학적인 방법으로 무모순성과 완전성에 관한 문제가 증명될 것이라고 진술했다 (힐베르트의 두 번째 문제).다비트 힐베르트는 유클리드의 공준을 데카르트 해석기하학의 대수적 참값으로 변환함으로써 유클리드 공준이 대수적 모형로 만족됨을 증명하였지만, 이는 여전히 다른 체계의 무모순성을 근거로 한 상대적 증명에 해당한다. 대수에 모순이 없다면 유클리드 기하학의 무모순성이 입증될 수 있을 것이므로, 산술체계의 무모순성을 확립하는 문제가 중요해진다.
다비트 힐베르트는 한 쪽 끝에 어떤 진술을 집어넣든지 간에, 크랭크를 돌리고 뒤로 물러앉아 있기만 하면 다른 쪽 끝에서 참/거짓이라는 대답이 나오는 진리기계(형식화된 공식체계)를 구상했다. 이는 수학을 형식화된 공식체계로 한 다음 그 체계의 무모순성을 ‘유한한 초수학적 방법’으로 증명함으로써 가능하다. 모든 산술적 진술의 참과 거짓을 결정할 수 있게 해주는 어떤 유한한 기계적 절차가 존재하느냐 하는 힐베르트의 결정문제에 대해, 형식화의 방법은 무한하게 많을 것이다. 괴델의 정리에 따르면 힐베르트 연구 계획의 모든 요구조건을 만족시키는 형식체계는 무한한 형식화의 모든 경우에 대해 존재하지도 않으며, 존재할 수도 없다.
힐베르트는 연역적인 체계를 형식화하려고 했다. 여기서 "형식화"란 체계 내의 표현식들의 '의미'를 제거하고 기호들의 연쇄체로 표시하는 것이다. 이 작업을 위해 힐베르트는 "수학"과 "초수학"을 구분했다. "초수학적 진술"이란, 메타 수학, 즉, 수학에 대한, 수학을 설명하는 언어에 속하는 것이다. 체계 안에서 사용된 부호에 대한 진술일 수도 있고, 체계 그 자체에 대한 진술일 수도 있다. 예를 들어 "1+1=2"는 수학에 속하는 것이지만, "'1+1=2'는 산술 공식이다."는 초수학에 속한다. "산술에 대한 이론 체계가 무모순이다." 또는 괴델의 불완전성 정리의 함축 같은 것도 모두 초수학에 속하는 것들이다.
《수학 원리》 및 수학의 형식화의 완성[편집]
형식화의 과정은 다음과 같다.
- 계산식에서 사용할 부호의 완전한 목록을 만든다(어휘에 해당).
- ‘공식’(문장)으로 용인 가능한 구성 규칙을 정한다(문법에 해당).
- 공식에서 다른 공식으로 변형시키는 추론규칙을 정한다.
- 어떤 공식을 그 체계의 기초, 토대가 되는 공리(원시공식)로 선별한다.
유클리드 기하학 뿐만 아니라 일반적인 수학 체계는 주세페 페아노 등에 의해 산술화되었고, 고틀로프 프레게, 버트런드 러셀 등 논리주의자들에 의해 산술체계가 논리학 명제로 표현될 수 있었다. 따라서 수학의 무모순성 문제는 형식논리학 자체의 무모순성 문제로 귀결되었고, 논리주의 진영의 앨프리드 노스 화이트헤드와 버트런드 러셀이 《수학 원리》에서 순수 수학(산술)의 모든 진술을 형식화하는 방법을 제공하였다. 《수학 원리》에 제시된 포괄적인 표기 체계에 따라 순수 수학에 속하는 모든 명제를 표준적인 방법에 맞추어 코드할 수 있다.
괴델의 증명[편집]
쿠르트 괴델은 1931년에 논문 〈《수학 원리》 및 관련 체계에서 형식적으로 결정될 수 없는 명제에 관하여 1〉(독일어: Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme I)[3] 에서 제1·제2 불완전성 정리를 증명하였고, 힐베르트 프로그램이 불가능하다는 것을 증명하였다. (제목과 달리, 2편은 출판되지 않았다.)이 정리는 수학의 체계를 완전하고 모순이 없는 공리계로 형식화하려는 힐베르트의 계획의 실패를 알리는 것으로 인식된다. 보다 구체적으로는, 이는 힐베르트의 두 번째 문제에 대한 부정적인 해답으로 볼 수도 있다.
괴델 이후의 증명[편집]
1943년에 스티븐 클레이니는 계산 가능성 이론을 사용하여, 정지 문제의 계산 불가능성으로부터 불완전성 정리를 재증명하였다.[4] 그레고리 차이틴(스페인어: Gregory J. Chaitin)은 1974년에 정보 이론에서의 차이틴 불완전성 정리를 증명하였으며,[5] 괴델의 불완전성 정리는 차이틴 불완전성 정리의 딸림정리로 쉽게 증명된다. 토르셸 프란센(스웨덴어: Torkel Franzén)은 힐베르트의 10번 문제의 부정적 해로부터 괴델의 불완전성 정리가 유도된다는 것을 보였다.[6]정의[편집]
제1 불완전성 정리[편집]
괴델의 제1 불완전성 정리의 내용은 다음과 같다. 공리계 및 추론 규칙으로 구성된 형식적 이론 은 다음 네 성질들을 동시에 만족시킬 수 없다.
은 다음 네 성질들을 동시에 만족시킬 수 없다.- (유효 생성성)
 의 공리계와 추론 규칙들은 재귀 열거 집합을 이룬다. 즉, 공리계가 유한하거나, 아니면 튜링 기계로 공리꼴로부터 생성되는 공리들을 열거할 수 있다.
의 공리계와 추론 규칙들은 재귀 열거 집합을 이룬다. 즉, 공리계가 유한하거나, 아니면 튜링 기계로 공리꼴로부터 생성되는 공리들을 열거할 수 있다. - (일관성)
 의 공리계로부터 거짓
의 공리계로부터 거짓  을 증명할 수 없다.
을 증명할 수 없다. - (산술의 표현 가능성)
 의 공리계로부터, 페아노 공리계와 동치인 공리들을 증명할 수 있다.
의 공리계로부터, 페아노 공리계와 동치인 공리들을 증명할 수 있다. - (산술에 대한 완전성) 자연수에 대한 모든 참인 명제는
 로부터 증명할 수 있다.
로부터 증명할 수 있다.
 은 부호수
은 부호수 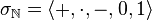 의 1차 논리 구조를 이룬다. 이 경우,
의 1차 논리 구조를 이룬다. 이 경우,  에서 참인 1차 논리
에서 참인 1차 논리  -명제들의 집합
-명제들의 집합  은 재귀 열거 집합이 아니다. (1차 논리의 경우, 괴델의 완전성 정리에 의하여 모형 이론적인 진리는 증명 이론적 진리와 일치한다.)
은 재귀 열거 집합이 아니다. (1차 논리의 경우, 괴델의 완전성 정리에 의하여 모형 이론적인 진리는 증명 이론적 진리와 일치한다.)마찬가지로, 이를 2차 논리의 증명 이론으로도 서술할 수 있다. 2차 논리에서는 페아노 공리계가 자연수 체계의 완전한 공리화를 이룬다. (즉, 페아노 공리계의 표준 모형(영어: standard model)은 자연수 집합밖에 없다.) 이 경우, 괴델의 제1 불완전성 정리에 따르면 페아노 공리의 2차 논리 체계는 (2차 논리의 표준 모형에서) 괴델 완전성 정리를 만족시키지 못한다. 즉, 2차 논리의 임의의 재귀 열거 가능 증명 이론에 대하여, 항상 페아노 공리로부터 증명할 수 없지만 참인
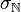 -명제가 존재한다. (물론, 2차 논리에서 헹킨 모형(영어: Henkin model)을 사용하면 적절한 증명 이론이 존재하지만, 헹킨 모형을 부여한 2차 논리는 사실상 1차 논리와 같으므로 이 경우 페아노 공리로부터 증명할 수 없지만 자연수에 대하여 참인 명제가 존재한다.)
-명제가 존재한다. (물론, 2차 논리에서 헹킨 모형(영어: Henkin model)을 사용하면 적절한 증명 이론이 존재하지만, 헹킨 모형을 부여한 2차 논리는 사실상 1차 논리와 같으므로 이 경우 페아노 공리로부터 증명할 수 없지만 자연수에 대하여 참인 명제가 존재한다.)제2 불완전성 정리[편집]
괴델의 제2 불완전성 정리의 내용은 다음과 같다. 공리계 및 추론 규칙으로 구성된 형식적 이론 은 다음 다섯 성질들을 동시에 만족시킬 수 없다.
은 다음 다섯 성질들을 동시에 만족시킬 수 없다.- (유효 생성성)
 의 공리계와 추론 규칙들은 재귀 열거 집합을 이룬다. 즉, 공리계가 유한하거나, 아니면 튜링 기계로 공리꼴로부터 생성되는 공리들을 열거할 수 있다.
의 공리계와 추론 규칙들은 재귀 열거 집합을 이룬다. 즉, 공리계가 유한하거나, 아니면 튜링 기계로 공리꼴로부터 생성되는 공리들을 열거할 수 있다. - (무모순성)
 의 공리계로부터 거짓
의 공리계로부터 거짓  을 증명할 수 없다.
을 증명할 수 없다. - (산술의 표현 가능성)
 의 공리계로부터, 페아노 공리계와 동치인 공리들을 증명할 수 있다.
의 공리계로부터, 페아노 공리계와 동치인 공리들을 증명할 수 있다. - (제1 정리의 표현 가능성)
 는 제1 불완전성 정리의 증명을 형식화할 수 있다.
는 제1 불완전성 정리의 증명을 형식화할 수 있다. - (무모순성의 증명 가능성)
 속에서,
속에서,  가 무모순적이라는 사실을 증명할 수 있다.
가 무모순적이라는 사실을 증명할 수 있다.
증명[편집]
제1 불완전성 정리의 증명[편집]
이론 의 명제들은 가산 무한 알파벳
의 명제들은 가산 무한 알파벳  로 기술된다고 하자. 예를 들어, 체르멜로-프렝켈 집합론의 경우 논리적 기호
로 기술된다고 하자. 예를 들어, 체르멜로-프렝켈 집합론의 경우 논리적 기호 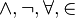 및 변수
및 변수 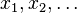 의 집합으로 삼을 수 있다. 즉, 모든 명제들은
의 집합으로 삼을 수 있다. 즉, 모든 명제들은  의 클레이니 스타
의 클레이니 스타 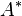 의 원소이다. (물론
의 원소이다. (물론 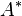 는 문법에 맞지 않는 기호열들을 포함하므로, 명제의 집합은
는 문법에 맞지 않는 기호열들을 포함하므로, 명제의 집합은 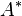 의 부분집합이다.) 그렇다면 명제의 괴델 수(영어: Gödel number)
의 부분집합이다.) 그렇다면 명제의 괴델 수(영어: Gödel number)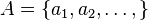 라고 하고,
라고 하고,  번째 소수를
번째 소수를 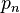 이라고 하면,
이라고 하면,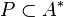 가
가  에서 증명 가능한 명제들의 집합이라고 하자. 그렇다면 그 상
에서 증명 가능한 명제들의 집합이라고 하자. 그렇다면 그 상 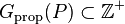 은 양의 정수의 부분집합이다.
은 양의 정수의 부분집합이다.또한,
 가 유효 생성 이론이라고 가정하였으므로, 모든 가능한 증명 또한 괴델 수를 부여할 수 있다. 즉, 증명의 집합을
가 유효 생성 이론이라고 가정하였으므로, 모든 가능한 증명 또한 괴델 수를 부여할 수 있다. 즉, 증명의 집합을 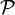 라고 한다면,
라고 한다면,  가 존재한다.
가 존재한다.페아노 공리계만을 사용하여, 다음과 같은 이항 관계
 를 정의하자.
를 정의하자.  는 다음을 의미한다.
는 다음을 의미한다. 는 어떤 자유 변수
는 어떤 자유 변수 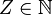 를 갖는 명제
를 갖는 명제 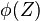 의 괴델 수이다. 즉,
의 괴델 수이다. 즉,  이다.
이다. 는 어떤 증명
는 어떤 증명  의 괴델 수이다. 즉,
의 괴델 수이다. 즉,  이다.
이다. 는
는 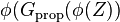 의 증명이다.
의 증명이다.
 를 갖는 명제를 생각할 수 있다.
를 갖는 명제를 생각할 수 있다. 가 이 명제를 증명할 수 있다면,
가 이 명제를 증명할 수 있다면,  는 모순적이다.
는 모순적이다. 가
가  를 증명할 수 있다고 가정하자. 그렇다면
를 증명할 수 있다고 가정하자. 그렇다면  의 증명
의 증명  가 존재한다. 이 증명
가 존재한다. 이 증명  의 괴델 수
의 괴델 수  에 대하여,
에 대하여,  가 성립한다. 따라서
가 성립한다. 따라서  는 거짓이다. 즉,
는 거짓이다. 즉,  는 거짓인 명제를 증명할 수 있으며,
는 거짓인 명제를 증명할 수 있으며,  는 모순된다.
는 모순된다. 가
가  를 증명할 수 없다고 가정하자. 그렇다면 정의에 따라
를 증명할 수 없다고 가정하자. 그렇다면 정의에 따라 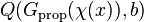 인
인  가 존재하지 않는다. 그렇다면 정의에 따라
가 존재하지 않는다. 그렇다면 정의에 따라  는 참이다. 따라서
는 참이다. 따라서  는 참인 명제를 증명할 수 없으며,
는 참인 명제를 증명할 수 없으며,  는 불완전하다.
는 불완전하다.
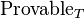 는
는  에서 증명할 수 있다는 뜻이다.
에서 증명할 수 있다는 뜻이다.제2 불가능성 정리의 증명[편집]
제1 불가능성 정리는 자연수에 대한 산술 명제이므로, 속의 한 명제로 나타낼 수 있다. 이 명제를
속의 한 명제로 나타낼 수 있다. 이 명제를 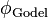 라고 쓰자. 또한,
라고 쓰자. 또한,  속에서
속에서  스스로가 무모순적이라는 명제를
스스로가 무모순적이라는 명제를 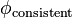 라고 쓰자. 그렇다면
라고 쓰자. 그렇다면정의에 따라서 다음과 같은 동치가 성립한다.
 속에서 증명할 수 있다. 제1 불가능성 정리의 증명을
속에서 증명할 수 있다. 제1 불가능성 정리의 증명을  속에서 재현하여, 함의
속에서 재현하여, 함의 속에서 증명할 수 있다. 따라서, 만약
속에서 증명할 수 있다. 따라서, 만약  속에서
속에서 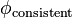 를 증명할 수 있다면
를 증명할 수 있다면  을
을  속에서 증명할 수 있다. 그러나 이는 제1 불완전성 정리에 의하여
속에서 증명할 수 있다. 그러나 이는 제1 불완전성 정리에 의하여  속에서 증명할 수 없다. 이는 모순이므로,
속에서 증명할 수 없다. 이는 모순이므로,  속에서
속에서 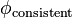 를 증명할 수 없다.
를 증명할 수 없다.참고 문헌[편집]
- 이동 ↑ Lewis, Florence P. (1920년 1월). “History of the parallel postulate” (영어). 《The American Mathematical Monthly》 27 (1): 16–23. doi:10.2307/2973238. JSTOR 2973238.
- 이동 ↑ Hilbert, David (1926). “Über das Unendliche” (독일어). 《Mathematische Annalen》 95: 161-90. doi:10.1007/BF01206605. ISSN 0025-5831. JFM 51.0044.02.
- 이동 ↑ Gödel, Kurt (1931). “Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme I” (독일어). 《Monatshefte für Mathematik und Physik》 38: 173-98. doi:10.1007/BF01700692. JFM 57.0054.02. Zbl 0002.00101.
- 이동 ↑ Kleene, Stephen Cole (1943). “Recursive predicates and quantifiers” (영어). 《Transactions of the American Mathematical Society》 53 (1): 41–73. doi:10.1090/S0002-9947-1943-0007371-8. ISSN 0002-9947. MR 0007371. Zbl 0063.03259.
- 이동 ↑ Chaitin, Gregory J. (1974년 7월). “Information-theoretic limitations of formal systems” (영어). 《Journal of the Association for Computing Machinery》 21: 403–424. doi:10.1145/321832.321839. ISSN 0004-5411. Zbl 0287.68027.
- 이동 ↑ Franzén, Torkel (2005). 《Gödel’s theorem: an incomplete guide to its use and abuse》 (영어). A.K. Peters. ISBN 1-56881-238-8. MR 2146326. Zbl 1081.03002.
- 네이글, 어니스트; 고중숙, 곽강제 역 (2010). 《호프스태터가 서문을 쓰고 개정한 괴델의 증명》 (한국어). 승산. ISBN 978-89-6139034-7.
- Nagel, Ernest; James R. Newman (2001년 10월). 《Gödel’s proof》 (영어) 2판. New York University Press. ISBN 978-081475816-8. Zbl 1101.03300.
- 클라인, 모리스 (2007). 《수학의 확실성》 (한국어). 사이언스 클래식 7. 심재관 역. 사이언스북스. ISBN 978-89-8371188-5.
- Kline, Morris (1980). 《Mathematics: the loss of certainty》 (영어). Oxford University Press. ISBN 0-19-502754-X. OCLC 6042956.
- 캐스티, 존; 베르너 드파울리 (2002). 《괴델》 (한국어). 박정일 역. 몸과마음. ISBN 978-89-8941819-4
|isbn=값 확인 필요 (도움말).- Casti, John L.; Werner DePauli (2001). 《Gödel: a life of logic, the mind, and mathematics》 (영어). Basic Books. ISBN 978-073820518-2.
- Goldstein, Rebecca (2005). 《Incompleteness: the proof and paradox of Kurt Gödel》 (영어). Great Discoveries. W. W. Norton & Company. ISBN 978-039305169-8.
- Davis, Martin (2006년 4월). “The incompleteness theorem” (영어). 《Notices of the American Mathematical Society》 53 (4): 414–418. Zbl 1100.03003.
- Hellman, Geoffrey (1981년 11월). “How to Gödel a Frege–Russell: Gödel’s incompleteness theorems and logicism” (영어). 《Noûs》 15 (4): 451–468. doi:10.2307/2214847. JSTOR 2214847.
- Berto, Francesco (2009년 11월). 《There’s something about Gödel: the complete guide to the incompleteness theorem》 (영어). Wiley-Blackwell. doi:10.1002/9781444315028. ISBN 978-1-4051-9766-3. Zbl 1183.03001.
- Smith, Peter (2013). 《An introduction to Gödel’s theorems》 (영어). Cambridge Introductions to Philosophy 2판. Cambridge University Press. doi:10.1017/CBO9781139149105. ISBN 978-1-107-02284-3. MR 3059012. Zbl 1270.03002.
바깥 고리[편집]
- Raatikainen, Panu (2013년 11월 11일). “Gödel's incompleteness theorems” (영어). 《Stanford Encyclopedia of Philosophy》.
- “Gödel incompleteness theorem” (영어). 《Encyclopedia of Mathematics》. Springer. 2001. ISBN 978-1-55608-010-4.
- Eric Wolfgang Weisstein. “Gödel's incompleteness theorem” (영어). 《Wolfram MathWorld》. Wolfram Research.
- Eric Wolfgang Weisstein. “Gödel's first incompleteness theorem” (영어). 《Wolfram MathWorld》. Wolfram Research.
- Eric Wolfgang Weisstein. “Gödel's second incompleteness theorem” (영어). 《Wolfram MathWorld》. Wolfram Research.
- Eric Wolfgang Weisstein. “Gödel number” (영어). 《Wolfram MathWorld》. Wolfram Research.



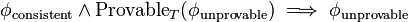
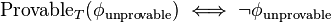

댓글 없음:
댓글 쓰기