2022년 7월 5일 한국 시간으로 오후 4시 20분경, 수학자로서 최고 권위의 상이자 최고의 영예라 할 수 있는 이른바 ‘수학 노벨상’, ‘필즈상(Fields Medal)’의 수상자가 발표되었다. 현재 미국 프린스턴 대 수학 교수와 한국고등과학원의 석학 교수를 겸하고 있는 허준이 교수가 이 영예의 수상을 받는 모습이 전 세계에 생중계되었다. 한국계 수학자가 필즈상을 받는 것은 이번이 최초이다.
노벨상보다 빛나는 필즈상의 영예
국제수학연맹(International Mathematical Union, IMU)에서는 수학 분야에 관한 토론과 강연 등의 교류가 이루어지는 국제 행사, 세계수학자대회(International Congress of Mathematicians, ICM)를 개최한다. 세계수학자대회는 올림픽과 마찬가지로 4년마다 열리며, 수학계에 중대한 공헌을 한 만 40세 미만의 수학자에게 필즈상을 수여한다.

필즈상의 전면에는 고대 그리스의 위대한 수학자인 아르키메데스의 두상이, 측면에는 허준이 교수의 영문 이름이 새겨져 있다. ©Wikipedia, International Mathematical Union 유튜브 캡처
필즈상이 ‘수학계의 노벨상’이라는 이명이 있다고는 하나, 실제로는 노벨상보다 더욱 받기 어렵다. 우선은 나이 제한이 큰 요인이다. 만 40세 미만이라는 나이 제한이 있는 이유는 ‘이룬 업적을 기리기 위해서’ 뿐만 아니라 동시에 ‘장래에도 계속해서 좋은 성과를 내도록 장려’하는 것이 필즈상 수여의 의미이기 때문이다. 허준이 교수는 1983년 6월생으로, 만 39세 나이로 필즈상을 수상했다.
또한 여러 분야에서 다수가 수상하는 노벨상과는 달리 필즈상은 최대 4명까지만 동시 수상할 수 있기 때문이다. 실제로도 1901년부터 시상한 역대 노벨상 수상자는 947명인 데 비해, 필즈상 수상자는 1936년부터 올해 2022년 수상자를 포함해도 64명에 불과한 극히 적은 수이다.
역사상 위대한 수학자 64인 안에 든 허준이 교수의 업적은 그 자체로도 대단하지만, 한국에서 자라 한국에서 교육받은 최초의 한국계 수학자 수상자라는 것과, 역대 아시아계 필즈상 수상자가 6명에 불과했으며 1990년 이후로는 전무했다는 점을 고려하면 그 의의가 크다고 할 수 있다. 이는 특히 올해 2월 한국의 수학국가등급이 상향되어 최고등급(5그룹) 12개국 안에 든 것에 연이은 희소식으로 한국 수학계에는 큰 기쁨이 되었다.
11개의 난제를 해결하다
서울대 물리천문학부에 재학하던 허준이 교수는 동대학원에서 수학 석사 학위를, 이후 미국 미시건 대에서 수학 박사 학위를 취득했다. 수학자들은 ‘난제(conjecture)’를 추측의 형태로 제시하는데, 대부분의 수학자들은 평생 하나의 난제를 해결하기도 힘들다. 그러나 허준이 교수는 40세가 되기도 전에 무려 11개의 난제를 증명하고 해결했다.
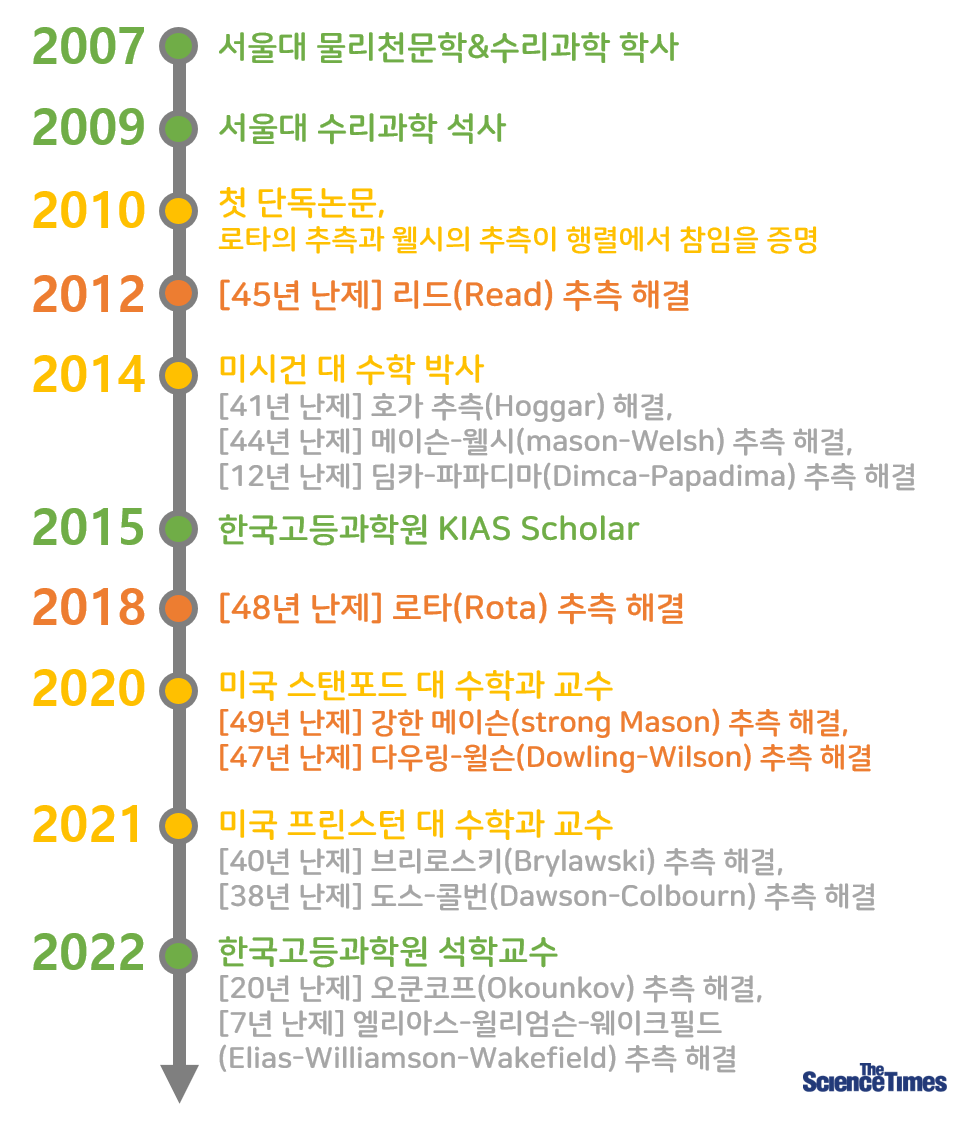
허준이 교수의 약력과 난제 해결 이력을 나타낸 도표이다. 박사학위를 취득하기 전에 오랜 수학 난제를 해결하며 수학계의 ‘스타’가 되었다. 서울대 수리과학부 김영훈 교수 출처 ©사이언스타임즈 김미경
박사 1년차에 불과한 2010년 첫 단독논문으로 수학계의 오랜 난제인 로타의 추측과 웰시의 추측이 행렬에서 참임을 증명한 것을 기점으로, 허준이 교수는 일약 수학계의 ‘스타’로 떠올랐다. 특히 박사학위를 받기도 전인 2012년에 수학계의 45년 난제인 ‘리드 추측’을 증명한 것은 허준이 교수의 천재성을 명확히 보여주었다. 리드 추측의 선행 연구(밀너 수 연구)는 서울대학교 석사과정에서부터 이미 시작했으며, 2015년부터 2021년까지 고등과학원의 방문교수(KIAS Scholar)로 있는 동안에도 많은 연구가 이루어진 것으로 알려져 있다.
허준이 교수의 연구 분야, 조합 대수 기하학이란?
허준이 교수의 연구 분야는 ‘조합 대수기하학(Combinatorial Algebraic Geometry)’으로 수학에서도 비교적 새로운 분야이다. 동시에 매우 어려운 분야이기도 한데, 서로 다른 두 분야를 자유롭게 넘나들려면 둘 모두에 정통해야 하기 때문이다.
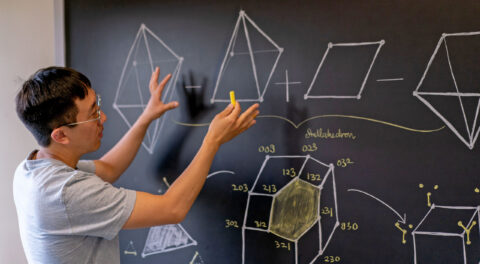
허준이 교수의 연구분야는 ‘조합 대수기하학’이다. 서로 다른 두 분야의 융합과 직관을 통해 많은 난제를 해결했다. ©International Mathematical Union 유튜브 캡처
조합론(Combinatorics)이란 간단히 말해 ‘경우의 수’를 탐구하는 것이다. 중‧고등학교 교육과정에서 배우는 경우의 수와 같은 맥락이다. 조합론의 주요 대상은 정수뿐 아니라 다각형과 각종 논리연산까지 포함된다. 특히, 각각의 객체들이 서로가 서로와 어떤 관계를 갖고 있는지를 표시함으로써 객체들의 ‘연결의 구조’를 다루는 ‘그래프 이론(graph theory)’는 컴퓨터 공학 및 구글 등 인터넷 검색 기술의 핵심 기반이 된다.
대수기하학(Algebraic Geometry)는 쉽게 말해 ‘도형’을 다루는 수학 분야이다. ‘대수’, 즉 식과 연산을 통해 ‘기하’, 도형, 곡선, 곡면 등을 연구한다. 역으로 도형 및 기하를 통해 식과 연산을 연구하기도 하며 그 사이의 관계를 탐구한다. 해석기하학의 심화라고도 할 수 있으며, 교육과정에서는 고등학교 과정의 ‘원의 방정식’을 예시로 들 수 있다.
허준이 교수는 대수기하학에 대한 강력한 직관을 바탕으로 조합론의 많은 난제들을 해결했다. 조합론 내부에서는 해결하지 못했던 문제들을 대수기하학과 접목시킴으로써 획기적인 해결을 보여주었다. 허준이 교수는 이에 대해 “조합된 객체들에서 공간을 상상하고 만들어내면, 기하학적 직관을 이용해서 원래 결합되어 있는 구조에 숨어있는 정보를 알아낼 수 있다”고 표현했다.
허준이 교수의 성과는 이후로도 많은 난제들을 이와 같은 방식으로 해결할 수 있다는 가능성을 보여줌은 물론, 조합론을 포괄하는 대수기하학의 구조가 존재할 수 있다는 것과 대수기하학의 토대가 더욱 확대될 수 있다는 것을 암시한다. 조합론과 대수기하학 두 분야에서 모두 새 지평을 연 것이다.
수학적 이론을 가볍게 살펴보면? 채색 다항식과 리드 추측
허준이 교수가 박사과정 중 해결한 난제 ‘리드 추측’과 조합 대수기하학은 조합론의 고전적인 문제인 ‘4색 문제’를 통해 살펴볼 수 있다. 4색 문제란 특정 여러 부분으로 나눈 평면에서 4개의 색깔을 서로 같은 색깔끼리 맞닿지 않게 색칠할 수 있느냐에 관한 것이다. 지도를 생각하면 각 나라를 4가지의 색깔로 이웃 나라와 겹치지 않게 색칠하는 것이다.
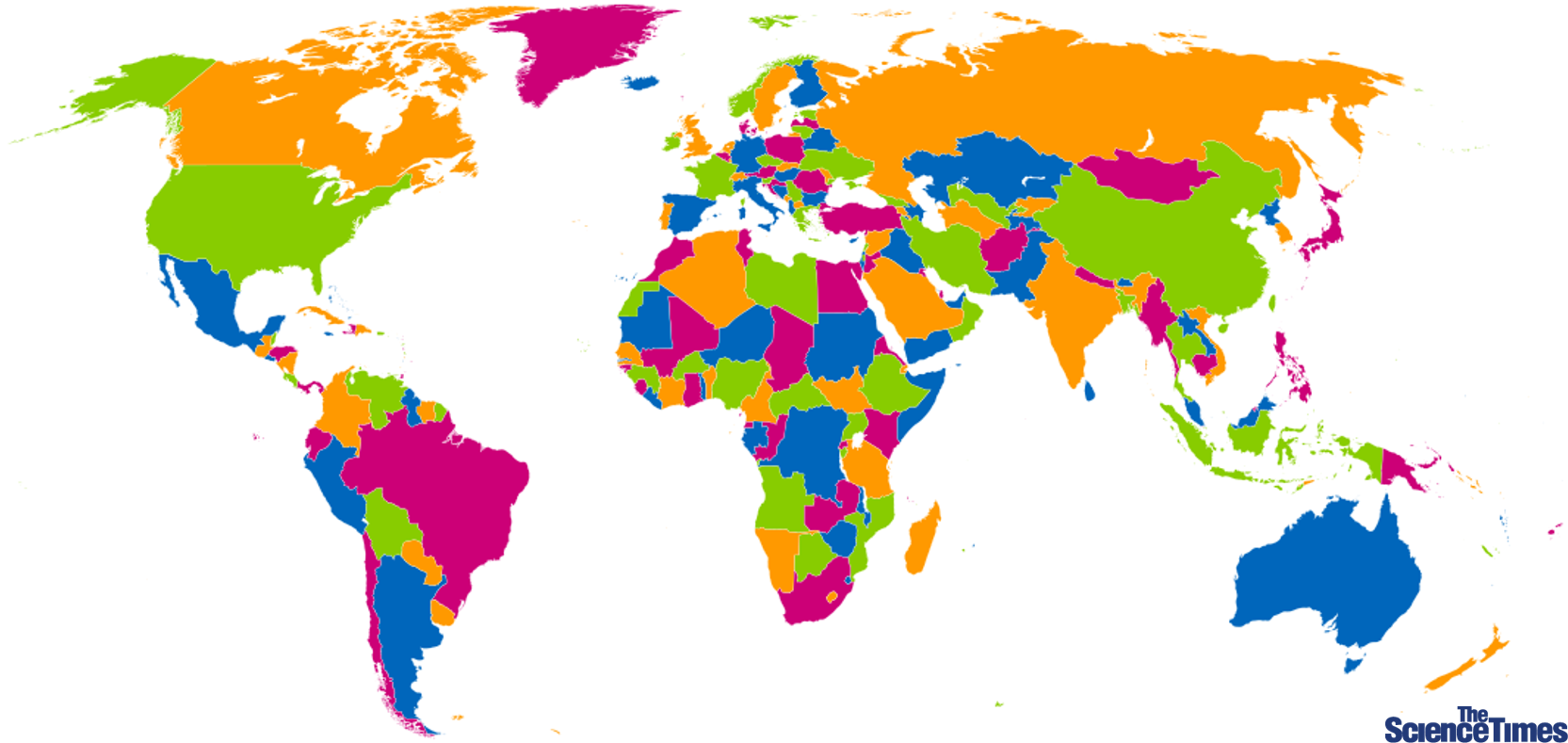
허준이 교수가 박사학위를 받기 전에 해결한 리드추측은 지도를 각기 다른 색으로 색칠하는 4색 문제로부터 출발한다. ©Wikimedia commons
이 문제를 다항식 또는 함수로 바꾸어보면 ‘조합론’에 ‘대수’ 또는 ‘대수기하’를 적용한 것이 된다. 각 구획의 연결성 및 관계성을 수식으로 만드는 것이다. 구획이 총 χ개일 때, 각기 다른 n개의 색깔을 겹치지 않게 색칠할 수 있는 경우의 수를 계산하는 식을 ‘채색 함수’ 또는 ‘채색 다항식’이라 한다.
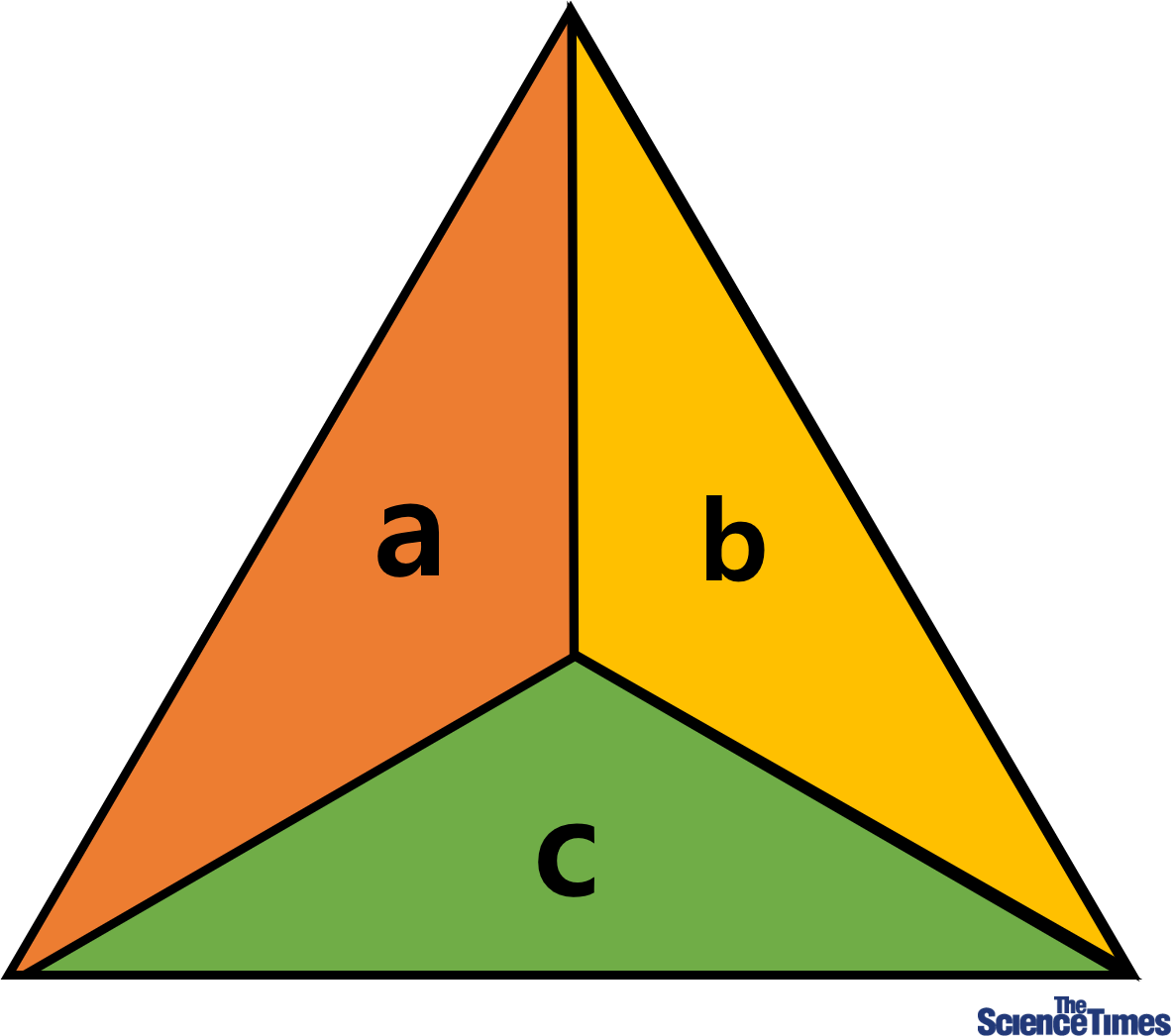
4색문제 또는 채색문제를 세 구획으로 나누어진 도형에서 보면 더욱 간단하다. ©사이언스타임즈 김미경
예컨대 위와 같은 그림의 삼각형의 세 구획에 적용해 본다면, 색칠할 수 있는 가짓수를 n개라고 했을 때, 삼각형을 각기 다르게 색칠할 수 있는 경우의 수는 ‘G(χ=3) = n(n-1)(n-2) = n³-3n²+2n’와 같이 표현할 수 있다. 이때 ‘4색 문제’라면 ‘n=4’이므로 총 가짓수는 6가지이다. 비교적 간단해 보이지만, 나눠진 구획이 많아질수록 다항식은 훨씬 복잡해진다.
허준이 교수는 이 다항식의 성질, 다항식 계수들의 증감 추세에 주목했다. 이 계수들의 로그 값 경향을 추론하여 리드 추측과 로타 추측 등 여러 난제들을 해결한 것이다. 이는 자연에서 얻는 많은 수열들이 로그를 씌웠을 때 특정 경향을 보인다는 것을 감안하면 더욱 의의가 크다고 할 수 있다.
특히 허준이 교수의 연구는 연결성과 독립성을 수학적으로 구조화한 ‘그래프(graph theorem)’와 ‘매트로이드(matroid)’의 성질에 관한 것인데, 따로따로 떨어진 점(객체)들의 연결을 구조화하고 수학적으로 표현한다는 점에서 여러 기술에 응용될 것으로 기대된다.
필즈상에 빛나는 수학적 성과, 우리 미래를 어떻게 바꿀까?
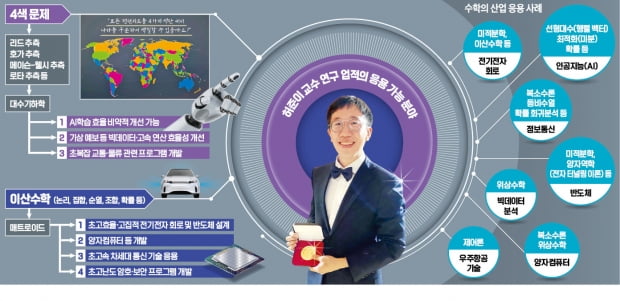
허준이 교수의 연구 업적은 여러 기술에 응용될 잠재력이 매우 크다. 컴퓨터 연산, AI, 빅데이터 등에 활용되는 알고리즘은 모두 조합론의 대표적인 응용 분야다. ‘연결’과 ‘구조’에 주목한 허준이 교수의 연구는 현대 사회에서 갖는 의미가 크다. 현대의 많은 기술이 통신과 네트워크, 복잡계 등과 연결되어 있기 때문이다.
이에 대해 허준이 교수는 “인터넷 사용자 하나를 꼭짓점으로 보고 이들이 연결되는 형태를 수학으로 해석할 수 있다”고 말했다. 허준이 교수의 석사과정 지도교수인 서울대 수리과학부 김영훈 교수 또한 “기초적인 그래프 이론의 활용이 구글 검색을 가능하게 했듯, 앞으로 허교수의 연구가 사람들의 생활을 혁명적으로 바꾸는 기술의 기초가 될 수 있다”고 말했다.

객체들의 ‘연결’에 주목하는 허준이 교수의 수학 연구 업적은 네트워크와 알고리즘이 중요한 현대사회와 기술에 크기 기여할 것으로 기대된다. ©GettyImagesBank
연구 업적들은 광대하고 복잡한 네트워크의 정보통신뿐 아니라, 반도체 설계, 교통, 물류, 통계물리 등 여러 분야에 밀접한 관련이 있어 파급효과가 클 것으로 기대된다. 검색 프로그램의 효율성을 높이는 데에 활용될 수도 있고, 빅데이터와 고속연산의 효율성을 높이거나 수많은 경우와 수많은 돌발 변수를 가정해야 하는 ‘초복잡계’의 교통.물류 관련 프로그램 개발, 기상 예보의 정확성 향상 등등 가능성은 무궁무진하다.
특히 AI(인공지능) 분야에서 크게 기여를 할 것으로 기대되는데, 리드 추측 해결 등의 성과를 활용함으로써 AI 학습의 효율성을 크게 높일 수 있기 때문이다. AI 학습에 필요한 데이터들의 변수는 노드, 즉 점의 형태로 나타나는데, 기존에는 AI의 신경망을 설계하는 단계에서 각 점(노드)들을 사람이 직접 선을 그리며 연결해야 했다. 그러나 허준이 교수의 수학적 이론을 적용하면 점을 연결하거나 연결을 끊는 작업들을 수식으로 표현하고 수학적 원리에 따라 수행할 수 있게 됨으로써, 훨씬 효율적인 AI 학습이 가능해진다. 현재 AI가 겪고 있는 한계를 뛰어넘고 비약적으로 발전해나갈 토대가 될 것으로 기대된다.
김영훈 교수는 “허 교수의 업적은 앞으로 100년간 IT와 AI 분야 발전에 지대한 영향을 미칠 것”이라며 “필즈상 수상과 같은 수학 분야 최정상급 연구는 수십 년에 걸쳐 활용되는 만큼 당장 어디에 활용할 수 있다고 말하는 것은 성급하지만, 10~20년 이내에 반드시 주요 산업에서 응용될 것”이라 말했다. 또한 “19세기 나온 리만기하학이 50년 뒤 상대성이론으로 이어졌고, 100년 뒤 GPS(위성항법장치)의 등장으로 이어졌듯, 허 교수의 업적도 미래의 삶을 바꾸는 데 큰 역할을 할 것”이라 덧붙였다.
허준이 교수는 2022년 영예의 필즈상을 수상함으로써 많은 수학자, 특히 한국의 수학자와 수학도들에게 큰 기쁨을 안겨주었다. 그리고 2022년 부로 한국고등과학원의 석학교수를 겸임하게 된 허준이 교수는 여름마다 방문하여 한국에서의 후학 양성에 힘쓰고 있다. 허준이 교수는 수학과 지식의 새로운 지평을 열어줬을 뿐 아니라 인류의 기술과 생활이 진보하는 기반 원리를 다져 주었다. 허준이 교수가 앞으로 계속해서 이어갈 다양한 연구를 통해 또 얼마나 세상을 놀라게 해줄 것인지 기대가 크다.
ScienceTimes










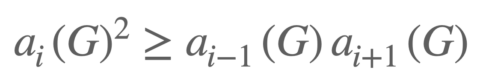





![허준이 교수가 푼 11개 난제, 어떻게 산업을 발전시키나 [김진원의 머니볼]](https://img.hankyung.com/photo/202207/01.30557086.1.jpg)
![허준이 교수가 푼 11개 난제, 어떻게 산업을 발전시키나 [김진원의 머니볼]](https://img.hankyung.com/photo/202207/01.30557085.1.jpg)
![허준이 교수가 푼 11개 난제, 어떻게 산업을 발전시키나 [김진원의 머니볼]](https://img.hankyung.com/photo/202207/01.30557094.1.jpg)
![허준이 교수가 푼 11개 난제, 어떻게 산업을 발전시키나 [김진원의 머니볼]](https://img.hankyung.com/photo/202207/01.30557096.1.jpg)
![허준이 교수가 푼 11개 난제, 어떻게 산업을 발전시키나 [김진원의 머니볼]](https://img.hankyung.com/photo/202207/01.30557087.1.jpg)
![허준이 교수가 푼 11개 난제, 어떻게 산업을 발전시키나 [김진원의 머니볼]](https://img.hankyung.com/photo/202207/01.30557090.1.jpg)
![허준이 교수가 푼 11개 난제, 어떻게 산업을 발전시키나 [김진원의 머니볼]](https://img.hankyung.com/photo/202207/01.30557088.1.jpg)
![허준이 교수가 푼 11개 난제, 어떻게 산업을 발전시키나 [김진원의 머니볼]](https://img.hankyung.com/photo/202207/01.30557091.1.jpg)
![허준이 교수가 푼 11개 난제, 어떻게 산업을 발전시키나 [김진원의 머니볼]](https://img.hankyung.com/photo/202207/01.30557093.1.jpg)
![허준이 교수가 푼 11개 난제, 어떻게 산업을 발전시키나 [김진원의 머니볼]](https://img.hankyung.com/photo/202207/01.30557092.1.jpg)