선택효과

두 명의 아이가 있는데, 한 아이는 분명 딸이라고 한다. 그러면서 다른 아이도 딸일 확률을 구해보라는 것이 문제다. 그런데 딸이라고 알려준 아이의 얼굴을 아느냐 모르느냐에 따라 답이 달라진다고 한다. 왜 이렇게 정보의 유무에 따라 답이 달라질까? <출처: Donnie Ray Jones at flickr.com>

“내 아이가 둘인디, 적어도 한 명은 딸이여.”

“그런가?”

“저기 지나가는 쟤가 내 딸이여.”

인심 좋은 어느 시골 마을에서 경찰로 근무하는 박종구 씨는 오랜만에 만난 친구에게 자신의 딸을 보여 주며 물었습니다. “내 다른 아이도 딸일 확률은 얼마겠나?”

종구 씨의 친구는 잠시 고민하다가 입을 열었습니다. “두 아이 모두 딸일 확률은….”

두 딸 문제는 답이 두 개?

자녀가 두 명인데, 둘 중 적어도 한 명은 딸인 상황에서 두 아이 모두 딸일 확률을 묻는 문제를 ‘두 딸 문제’라고 한다. 단순한 문제처럼 보이지만 이 문제가 처음 등장한 1959년 이래로 두 가지 답이 팽팽하게 맞서고 있다. 수학 문제에 어떻게 답이 두 개일 수 있을까?

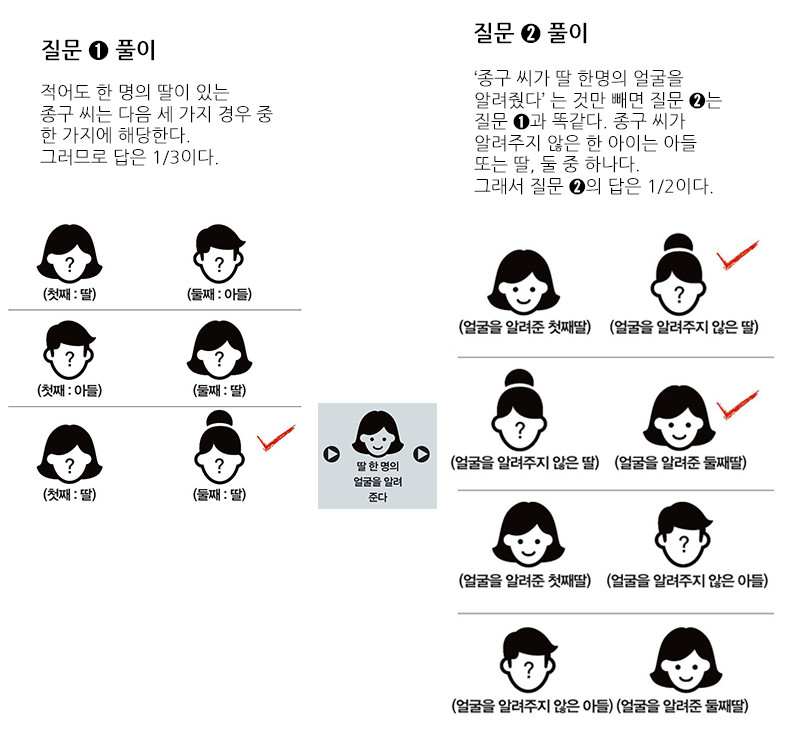
질문 ➊
두 자녀가 있는 종구 씨. 두 자녀 중 적어도 한 명은 딸이다. 이때 두 자녀 모두 딸일 확률은?

질문 ➋
두 자녀가 있는 종구 씨. 두 자녀 중 적어도 한 명은 딸이다. 종구 씨가 한 아이를 가리키며 ‘쟤가 내 딸이야’라고 알려준다. 이때 두 자녀 모두 딸일 확률은?
(단, 항상 둘째가 딸이거나 아들일 확률이 첫째의 성별에 영향을 받지 않는다고 가정한다.)

여기까지만 보면 두 질문에 대한 답에 특별한 문제는 없는 것 같다. 독자 여러분도 아무런 오류가 없다고 생각한다면, ‘딸 한 명의 얼굴을 알게 되면 나머지 아이가 딸일 확률이 바뀐다’는 말에도 동의하는 것이다.

혹시 이 말이 어딘가 이상하게 느껴질 수도 있다. 딸 한 명의 얼굴을 알게 되더라도 또 다른 자녀가 여자 아이일 확률은 그대로여야 하지 않을까? 스크롤을 내리기 전에 어느 쪽인지 생각해보시길.

얼굴 알면 확률이 바뀐다고?

“우리 딸 얼굴을 알기 전이든 알고 난 다음이든 다른 아이도 딸일 확률은 똑같을 것 같으면, 질문 ➋를 다르게 풀어야제~.”

종구 씨는 혼란에 빠진 친구에게 힌트를 줬다. “내가 아들만 둘이면 ‘쟤가 내 딸이여’라고 말을 못했겄지?”

두 자녀의 성별 조합은 (아들, 아들), (딸, 아들), (아들, 딸), (딸, 딸)이며 각 경우의 확률은 1/4로 모두 같다. 종구 씨는 적어도 딸이 한 명 있기 때문에 (아들, 아들)인 경우를 뺀 셋 중 한 가지 경우에 해당한다. 즉, 두 아이 모두 딸일 확률은 1/3이다. 이때 종구 씨가 가리킨 딸이 첫째인지, 둘째인지를 따져서 (딸, 딸)을 2가지로 세면 안 된다. 자녀가 (딸, 딸)이면서 종구 씨가 첫째를 가리켰을 확률은 1/4×1/2인데, 경우의 수를 셀 때 각 경우의 발생 확률이 모두 같아야 한다. 즉 확률이 1/4인 다른 경우와 똑같이 셀 수 없다. 그렇다면 과연 질문 ➋의 답은 1/2일까, 1/3일까? 또는 둘 다 맞을까?

동전 문제로 생각해보자

질문 ➋와 똑같은 동전 문제로 상황을 분석해보자.

동전 문제

수동이와 고리포터가 동전 던지기 게임을 한다. 수동이가 10원짜리와 100원짜리 동전을 동시에 던지는데, 만약 둘 다 뒷면이 나오면 적어도 한 면은 앞면이 나올 때까지 동전을 다시 던지기로 한다. 수동이는 앞면이 나온 동전 하나를 고리포터에게 보여주고, 나머지 동전은 손바닥으로 가린다. 이때, 수동이가 손으로 가린 동전도 앞면일 확률은?
(단, 그림이 있는 면이 앞면, 숫자가 있는 면이 뒷면이다.)

‘동전이 앞면이 나오는 상황’을 ‘자녀가 딸인 상황’과 같다고 보면 이 동전 문제는 질문 ➋와 똑같다. 물론 질문 ➋에서 가정한 두 가지 사항도 동전 문제에 똑같이 적용된다. 둘째 아이의 성별이 첫째 아이의 성별에 영향을 받지 않는다는 가정처럼 동전 하나가 앞면이 나올지, 뒷면이 나올지도 다른 동전에 영향을 받지 않는다. 또한, 한 아이의 성별이 아들일지 딸일지는 각각 확률이 50%인데, 동전도 앞면이 나올 확률과 뒷면이 나올 확률이 각각 50%다.

➊ 수동이가 어느 동전을 보여줄지 결정하면 1/3이 정답!
만약 수동이가 두 동전을 던진 다음 ‘상황을 모두 확인하고 나서’ 앞면이 나온 동전 하나만 고리포터에게 보여준다면, 손으로 가린 다른 동전이 앞면일 확률은 1/3이다.

수동이가 두 동전이 각각 어느 면이 나왔는지 모두 알고 있고, 그 중 앞면인 동전을 직접 골라 보여주는 이 상황은, 종구 씨가 두 자녀 가운데 딸인 아이 한 명을 콕 집어서 친구에게 보여주는 상황과 같다. 즉, 질문 ➋를 이 경우라고 생각한다면 종구 씨가 딸 한 명의 얼굴을 보여줬더라도 두 자녀가 모두 딸일 확률은 1/3이다.

➋ 고리포터가 어느 동전을 볼지 결정하면 1/2이 정답!
이번에는 동전은 수동이가 던지되, 어느 동전을 볼지는 고리포터가 결정하기로 하자. 고리포터는 두 동전의 상태를 모르는 채로 10원짜리와 100원짜리 동전 중에 무엇을 볼 것인지를 고른다. 만약 우연히 뒷면이 나온 동전을 고른다면 이 게임 자체가 성립되지 않는다. 앞면이 나온 동전을 봤을 때 나머지 동전이 앞면일 확률을 구하는 문제이기 때문이다. 예를 들어, 고리포터가 10원짜리 동전의 앞면을 봤다면 수동이가 손으로 가린 100원짜리 동전도 앞면일 확률은 1/2이다. 100원짜리 동전의 앞면을 봤어도 수동이가 손으로 가린 10원짜리 동전이 앞면일 확률 역시 1/2이다.

이 상황은 종구 씨가 길을 가는 딸을 우연히 발견하고 친구에게 소개하는 상황과 같다. 우연히 만난 딸을 소개했을 뿐, 두 자녀 중 누구를 소개할지 고를 수 없었던 것이다. 질문 ➋를 이렇게 생각한다면 친구에게 딸의 얼굴을 알려주는 행위가 두 자녀 모두 딸일 확률을 1/2로 바꾸는 셈이 된다.

‘쟤가 딸이다’, ‘동전이 앞면이 나왔다’와 같은 정보를 우연히 준 건지, 정보를 주는 사람이 의도에 맞게 뽑아서 준 건지에 따라 답이 달라지는 현상을 ‘선택효과’라고 한다. 한 가지 문제를 여러 가지 상황으로 해석해서 나온 두 가지 답을 인정할지, 한 가지 문제에는 오직 한 가지 답만 인정할지 논리학자들 사이에서도 의견이 분분하다. 여러분의 의견은 어느 쪽인가?

네이버캐스트