2016년
3월 15일, 영국 옥스퍼드대 수학연구소의 앤드루 와일스 교수가 2016년 아벨상 수상자로 선정되었다. 와일스는 2016년 5월24일,
노르웨이의 수도 오슬로에서 상을 받았다. 필즈상과 더불어 수학계의 노벨상이라 불리는 이 상을 앤드루 와일스가 받는 것에 아무도 이견이 없을
것이다. 그는 약 350년간 풀리지 않았던 ‘페르마의 마지막 정리’를 최초로 증명했기 때문이다.
‘페르마의
마지막 정리(영어로는 Fermat’s Last Theorem,
이하FLT)’는
보기에는 쉽지만 증명은 결코 쉽지 않은 문제의 대표적인 예다. 수학을 취미삼아 연구했던 17세기 프랑스의 법률가 피에르 드 페르마는 피타고라스의
정리(x2+y2=z2)를 약간 다르게 바꾼
식을 자신이 읽고 있던 책의 귀퉁이에 써 놓았다.
xn+yn=zn
n이 3 이상의 정수일 때, 이 방정식을 만족하는 정수 x, y, z는 존재하지 않는다.
n이 3 이상의 정수일 때, 이 방정식을 만족하는 정수 x, y, z는 존재하지 않는다.
아주
간단한 이 문장이 바로 FLT다.
아마추어 수학자가 증명없이 남긴 이 정리를 증명하기 위해 수많은 수학자가 도전했지만 번번이 실패했다. FLT는
19세기에도 난해한 문제로 유명했는데, 마지막까지 아무도 증명하지 못해 마지막 정리라고 부르게 된 것이다. ‘수학의 왕자’로 불렸던
가우스도 FLT를
‘정리의 진위 여부를 증명할 수 없는 수학정리’라고 언급했다.
이
문제를 증명한 것이 바로 ‘앤드루 와일스’다. 그는 열 살이던 1963년에 에릭 템플 벨이 쓴 <최후의 문제>라는 책에서 FLT를
처음 발견했다. 사이먼 싱의 책 <페르마의 마지막 정리>에서 와일스는 어린 자신도 이해할 만큼 간단한 문제가 아직도 풀리지 않고
남아있다는 점이 그의 호기심을 자극했다고 밝혔다. 하지만 당시에 앤드루 와일스가 언젠가 이 문제를 풀어내리라고는 아무도 생각하지
못했다.
1957년
일본인 수학자 타니야마 유타카와 시무라 고로는 ‘모든 타원방정식은 모듈 형태와 하나씩 대응되는 관계다’라는 ‘타니야마-시무라 추론’을 떠올렸다.
이들은 이 추론을 뒷받침하는 증거를 찾으려고 노력했지만, 증명은 하지 못했다.
1984년,
독일 수학자 게르하르트 프라이가 최초로 페르마의 방정식(An+Bn=Cn)을 타원방정식
형태(y2=x3+(An-Bn)x2-AnBn)로 바꿀 수 있다고
발표했다. 프라이가 만든 방정식 덕분에 수학자들은 타니야마-시무라 추론과 페르마의 마지막 정리 사이에 어떤 관계가 있을지도 모른다는 생각을 하게
됐다.
1986년,
프라이의 발표를 들은 미국 수학자 켄 리벳은 프라이가 만든 타원 방정식이 ‘모든 타원방정식을 모듈 형태로 바꿀 수 있다’는 타니야마-시무라
추론을 깨는 예임을 알아냈다. 만약 타니야마-시무라 추론이 맞다면 프라이의 방정식은 존재할 수 없는 식이고, 다시 말해 페르마의
방정식(An+Bn=Cn)은 성립할 수 없다.
즉, 타니야마-시무라 추론이 맞다는 것을 증명하면 (An+Bn=Cn)을 만족하는 정수해는
존재하지 않는다는 페르마의 마지막 정리를 증명하게 되는 셈이다.
1993년
앤드루 와일스는 타니야마-시무라 추론을 증명해냈다. 즉, 페르마의 마지막 정리를 증명한 것이다. 그는 강연을 통해 이 연구 결과를 발표했고,
페르마의 마지막 정리가 증명됐다는 소식은 전 세계로 퍼져나갔다.
와일스는
영국 케임브리지에 있는 아이작 뉴턴 연구소에서 열리는 세미나에서 오랜 연구의 결실을 발표하기로 마음먹었다. 강연 제목은 ‘모듈 형태,
타원방정식, 그리고 갈루아 군의 표현’으로, 여러 수학자가 참석하는 세미나의 프로그램 중 하나였다. 주최측의 배려로 특별히 와일스만 며칠 동안
세 번에 걸쳐 강연을 할 수 있었다.
와일스는
강연 직전까지도 무엇을 증명했는지 밝히지 않았고, 첫 번째와 두 번째 강연을 들은 동료 수학자들 역시 그가 정확히 무엇을 말하려는지 알지
못했다. 동료들은 이메일을 통해 마지막 강연에 대한 기대감을 나타냈다.
마지막
강연이 있었던 1993년 6월 23일, 와일스의 강연장에는 200여 명의 청중이 몰려들었다. 와일스는 훌륭한 아이디어를 완성한 켄 리벳을 포함한
여러 수학자와 대학원생 앞에서 증명을 완성해 나갔다. 증명을 끝내고 페르마의 마지막 정리를 칠판에 쓴 그는 “이쯤에서 끝내는 게 좋겠습니다”라고
말하며 발표를 마쳤다. 순간 우레와 같은 함성과 박수갈채가 쏟아졌다.
와일스는
페르마의 마지막 정리를 증명한 업적을 인정받아 국제수학연맹이 수여하는 기념 은판, 울프상, 쇼상 등 각종 상의 주인이 됐다. 이런 와일스에게
아벨상이 수여된다는 소식은 페르마의 마지막 정리에 대한 도전 정신과 그의 증명이 얼마나 아름다운지를 다시 한 번 보여준다.
수학동아



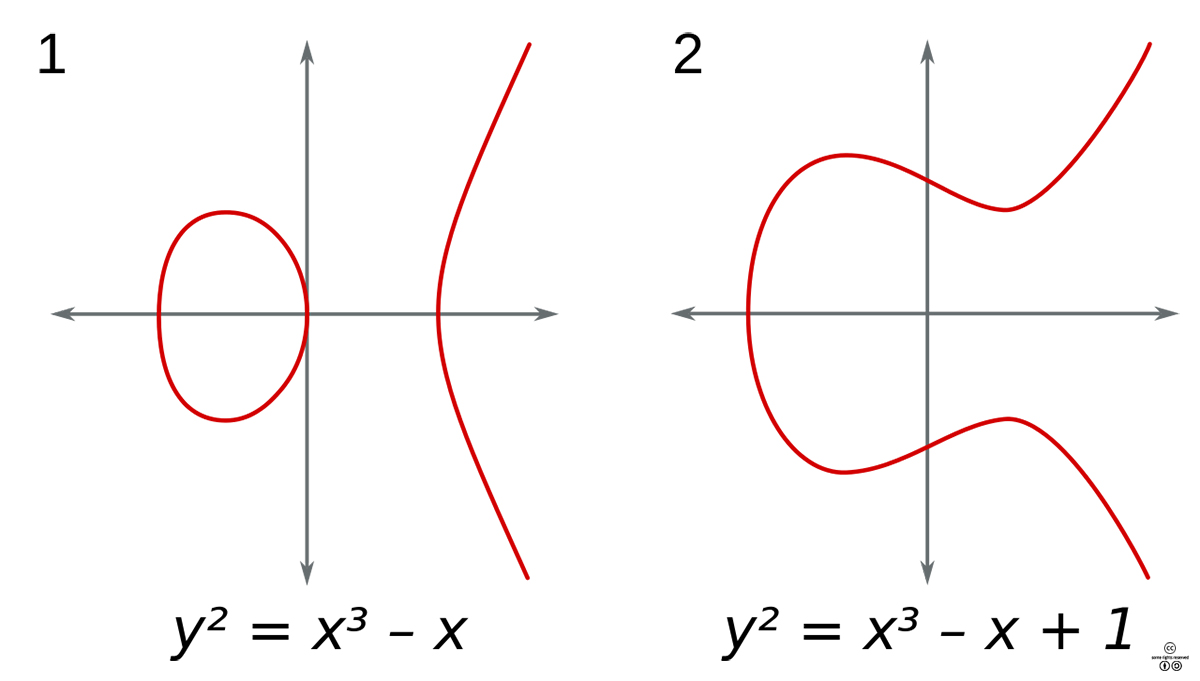

댓글 없음:
댓글 쓰기