geometric series

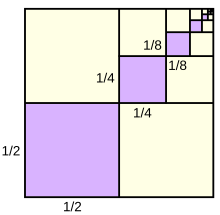
In mathematics, a geometric series is a series with a constant ratio between successive terms. For example, the series

${\displaystyle {\frac {1}{2}}\,+\,{\frac {1}{4}}\,+\,{\frac {1}{8}}\,+\,{\frac {1}{16}}\,+\,\cdots }$

is geometric, because each successive term can be obtained by multiplying the previous term by 1/2.

Geometric series are among the simplest examples of infinite series with finite sums, although not all of them have this property. Historically, geometric series played an important role in the early development of calculus, and they continue to be central in the study of convergence of series. Geometric series are used throughout mathematics, and they have important applications in physics, engineering, biology, economics, computer science, queueing theory, and finance.

Each of the purple squares has 1/4 of the area of the next larger square (1/2×1/2 = 1/4, 1/4×1/4 = 1/16, etc.). The sum of the areas of the purple squares is one third of the area of the large square.

Why "Geometric" Sequence?

Because it is like increasing the dimensions in geometry:

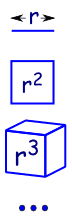	a line is 1-dimensional and has a length of r
	in 2 dimensions a square has an area of r2
	in 3 dimensions a cube has volume r3
	etc (yes we can have 4 and more dimensions in mathematics).

Geometric Sequences are sometimes called Geometric Progressions (G.P.’s)

Common ratio[edit]

The convergence of the geometric series with r=1/2 and a=1/2

The convergence of the geometric series with r=1/2 and a=1

The terms of a geometric series form a geometric progression, meaning that the ratio of successive terms in the series is constant. This relationship allows for the representation of a geometric series using only two terms, r and a. The term r is the common ratio, and a is the first term of the series. As an example the geometric series given in the introduction,

${\displaystyle {\frac {1}{2}}\,+\,{\frac {1}{4}}\,+\,{\frac {1}{8}}\,+\,{\frac {1}{16}}\,+\,\cdots }$

may simply be written as

${\displaystyle a+ar+ar^{2}+ar^{3}+\cdots }$ , with ${\displaystyle a={\frac {1}{2}}}$ and ${\displaystyle r={\frac {1}{2}}}$.

The following table shows several geometric series with different start terms and common ratios:

Start term, a	Common ratio, r	Example series
4	10	4 + 40 + 400 + 4000 + 40,000 + ···
9	1/3	9 + 3 + 1 + 1/3 + 1/9 + ···
7	1/10	7 + 0.7 + 0.07 + 0.007 + 0.0007 + ···
3	1	3 + 3 + 3 + 3 + 3 + ···
1	−1/2	1 − 1/2 + 1/4 − 1/8 + 1/16 − 1/32 + ···
3	–1	3 − 3 + 3 − 3 + 3 − ···

The behavior of the terms depends on the common ratio r:

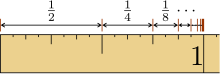
If r is between −1 and +1, the terms of the series approach zero in the limit (becoming smaller and smaller in magnitude), and the series converges to a sum. In the case above, where r is 1/2, the series converges to 1.

If r is greater than one or less than minus one the terms of the series become larger and larger in magnitude. The sum of the terms also gets larger and larger, and the series has no sum. (The series diverges.)

If r is equal to one, all of the terms of the series are the same. The series diverges.

If r is minus one the terms take two values alternately (e.g. 2, −2, 2, −2, 2,... ). The sum of the terms oscillates between two values (e.g. 2, 0, 2, 0, 2,... ). This is a different type of divergence and again the series has no sum. See for example Grandi's series: 1 − 1 + 1 − 1 + ···.

Sum[edit]

The sum of a geometric series is finite as long as the absolute value of the ratio is less than 1; as the numbers near zero, they become insignificantly small, allowing a sum to be calculated despite the series containing infinitely many terms. The sum can be computed using the self-similarity of the series.

Example[edit]

Visual derivation of the sum of infinite terms of a geometric series

Consider the sum of the following geometric series:

${\displaystyle s\;=\;1\,+\,{\frac {2}{3}}\,+\,{\frac {4}{9}}\,+\,{\frac {8}{27}}\,+\,\cdots .}$

This series has common ratio 2/3. If we multiply through by this common ratio, then the initial 1 becomes a 2/3, the 2/3 becomes a 4/9, and so on:

${\displaystyle {\frac {2}{3}}s\;=\;{\frac {2}{3}}\,+\,{\frac {4}{9}}\,+\,{\frac {8}{27}}\,+\,{\frac {16}{81}}\,+\,\cdots .}$

This new series is the same as the original, except that the first term is missing. Subtracting the new series (2/3)s from the original series s cancels every term in the original but the first,

${\displaystyle s\,-\,{\frac {2}{3}}s\;=\;1,\;\;\;{\mbox{so }}s=3.}$

A similar technique can be used to evaluate any self-similar expression.

Formula[edit]

For ${\displaystyle r\neq 1}$, the sum of the first n terms of a geometric series is

${\displaystyle a+ar+ar^{2}+ar^{3}+\cdots +ar^{n-1}=\sum _{k=0}^{n-1}ar^{k}=a\left({\frac {1-r^{n}}{1-r}}\right),}$

where a is the first term of the series, and r is the common ratio. We can derive this formula as follows:

${\displaystyle {\begin{aligned}s&=a+ar+ar^{2}+ar^{3}+\cdots +ar^{n-1},\\rs&=ar+ar^{2}+ar^{3}+ar^{4}+\cdots +ar^{n},\\s-rs&=a-ar^{n},\\s(1-r)&=a(1-r^{n}),\end{aligned}}}$

so,

${\displaystyle s=a\left({\frac {1-r^{n}}{1-r}}\right)\quad {\text{(if }}r\neq 1{\text{)}}.}$

As n goes to infinity, the absolute value of r must be less than one for the series to converge. The sum then becomes

${\displaystyle a+ar+ar^{2}+ar^{3}+ar^{4}+\cdots =\sum _{k=0}^{\infty }ar^{k}={\frac {a}{1-r}},{\text{ for }}|r|<1.}$

When a = 1, this can be simplified to

${\displaystyle 1\,+\,r\,+\,r^{2}\,+\,r^{3}\,+\,\cdots \;=\;{\frac {1}{1-r}},}$

the left-hand side being a geometric series with common ratio r.

The formula also holds for complex r, with the corresponding restriction, the modulus of r is strictly less than one.

Proof of convergence[edit]

We can prove that the geometric series converges using the sum formula for a geometric progression:

${\displaystyle {\begin{aligned}1+r+r^{2}+r^{3}+\cdots \ &=\lim _{n\rightarrow \infty }\left(1+r+r^{2}+\cdots +r^{n}\right)\\&=\lim _{n\rightarrow \infty }{\frac {1-r^{n+1}}{1-r}}.\end{aligned}}}$

Since (1 + r + r² + ... + rⁿ)(1−r) = 1−rⁿ⁺¹ and rⁿ⁺¹ → 0 for | r | < 1.

Convergence of geometric series can also be demonstrated by rewriting the series as an equivalent telescoping series. Consider the function,

${\displaystyle g(K)={\frac {r^{K}}{1-r}}.}$

Note that

${\displaystyle 1=g(0)-g(1)\ ,\ r=g(1)-g(2)\ ,\ r^{2}=g(2)-g(3)\ ,\ldots }$

Thus,

${\displaystyle S=1+r+r^{2}+r^{3}+\cdots =(g(0)-g(1))+(g(1)-g(2))+(g(2)-g(3))+\cdots .}$

If

${\displaystyle |r|<1}$

then

${\displaystyle g(K)\longrightarrow 0{\text{ as }}K\to \infty .}$

So S converges to

${\displaystyle g(0)={\frac {1}{1-r}}.}$

Applications[edit]

Repeating decimals[edit]

Main article: Repeating decimal

A repeating decimal can be thought of as a geometric series whose common ratio is a power of 1/10. For example:

${\displaystyle 0.7777\ldots \;=\;{\frac {7}{10}}\,+\,{\frac {7}{100}}\,+\,{\frac {7}{1000}}\,+\,{\frac {7}{10000}}\,+\,\cdots .}$

The formula for the sum of a geometric series can be used to convert the decimal to a fraction,

${\displaystyle 0.7777\ldots \;=\;{\frac {a}{1-r}}\;=\;{\frac {7/10}{1-1/10}}\;=\;{\frac {7/10}{9/10}}\;=\;{\frac {7}{9}}.}$

The formula works not only for a single repeating figure, but also for a repeating group of figures. For example:

${\displaystyle 0.123412341234\ldots \;=\;{\frac {a}{1-r}}\;=\;{\frac {1234/10000}{1-1/10000}}\;=\;{\frac {1234/10000}{9999/10000}}\;=\;{\frac {1234}{9999}}.}$

Note that every series of repeating consecutive decimals can be conveniently simplified with the following:

${\displaystyle 0.09090909\ldots \;=\;{\frac {09}{99}}\;=\;{\frac {1}{11}}.}$

${\displaystyle 0.143814381438\ldots \;=\;{\frac {1438}{9999}}.}$

${\displaystyle 0.9999\ldots \;=\;{\frac {9}{9}}\;=\;1.}$

That is, a repeating decimal with repeat length n is equal to the quotient of the repeating part (as an integer) and 10ⁿ - 1.

Archimedes' quadrature of the parabola[edit]

Archimedes' dissection of a parabolic segment into infinitely many triangles

Main article: The Quadrature of the Parabola

Archimedes used the sum of a geometric series to compute the area enclosed by a parabola and a straight line. His method was to dissect the area into an infinite number of triangles.

Archimedes' Theorem states that the total area under the parabola is 4/3 of the area of the blue triangle.

Archimedes determined that each green triangle has 1/8 the area of the blue triangle, each yellow triangle has 1/8 the area of a green triangle, and so forth.

Assuming that the blue triangle has area 1, the total area is an infinite sum:

${\displaystyle 1\,+\,2\left({\frac {1}{8}}\right)\,+\,4\left({\frac {1}{8}}\right)^{2}\,+\,8\left({\frac {1}{8}}\right)^{3}\,+\,\cdots .}$

The first term represents the area of the blue triangle, the second term the areas of the two green triangles, the third term the areas of the four yellow triangles, and so on. Simplifying the fractions gives

${\displaystyle 1\,+\,{\frac {1}{4}}\,+\,{\frac {1}{16}}\,+\,{\frac {1}{64}}\,+\,\cdots .}$

This is a geometric series with common ratio 1/4 and the fractional part is equal to

${\displaystyle \sum _{n=0}^{\infty }4^{-n}=1+4^{-1}+4^{-2}+4^{-3}+\cdots ={4 \over 3}.}$

The sum is

${\displaystyle {\frac {1}{1-r}}\;=\;{\frac {1}{1-{\frac {1}{4}}}}\;=\;{\frac {4}{3}}.}$

This computation uses the method of exhaustion, an early version of integration. Using calculus, the same area could be found by a definite integral.

Fractal geometry[edit]

The interior of the Koch snowflake is a union of infinitely many triangles.

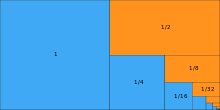
In the study of fractals, geometric series often arise as the perimeter, area, or volume of a self-similar figure.

For example, the area inside the Koch snowflake can be described as the union of infinitely many equilateral triangles (see figure). Each side of the green triangle is exactly 1/3 the size of a side of the large blue triangle, and therefore has exactly 1/9 the area. Similarly, each yellow triangle has 1/9 the area of a green triangle, and so forth. Taking the blue triangle as a unit of area, the total area of the snowflake is

${\displaystyle 1\,+\,3\left({\frac {1}{9}}\right)\,+\,12\left({\frac {1}{9}}\right)^{2}\,+\,48\left({\frac {1}{9}}\right)^{3}\,+\,\cdots .}$

The first term of this series represents the area of the blue triangle, the second term the total area of the three green triangles, the third term the total area of the twelve yellow triangles, and so forth. Excluding the initial 1, this series is geometric with constant ratio r = 4/9. The first term of the geometric series is a = 3(1/9) = 1/3, so the sum is

${\displaystyle 1\,+\,{\frac {a}{1-r}}\;=\;1\,+\,{\frac {\frac {1}{3}}{1-{\frac {4}{9}}}}\;=\;{\frac {8}{5}}.}$

Thus the Koch snowflake has 8/5 of the area of the base triangle.

Zeno's paradoxes[edit]

Main article: Zeno's paradoxes

The convergence of a geometric series reveals that a sum involving an infinite number of summands can indeed be finite, and so allows one to resolve many of Zeno's paradoxes. For example, Zeno's dichotomy paradox maintains that movement is impossible, as one can divide any finite path into an infinite number of steps wherein each step is taken to be half the remaining distance. Zeno's mistake is in the assumption that the sum of an infinite number of finite steps cannot be finite. This is of course not true, as evidenced by the convergence of the geometric series with ${\displaystyle r=1/2}$.

Euclid[edit]

Book IX, Proposition 35^[1] of Euclid's Elements expresses the partial sum of a geometric series in terms of members of the series. It is equivalent to the modern formula.

Common ratio[edit]

The convergence of the geometric series with r=1/2 and a=1/2

The convergence of the geometric series with r=1/2 and a=1

The terms of a geometric series form a geometric progression, meaning that the ratio of successive terms in the series is constant. This relationship allows for the representation of a geometric series using only two terms, r and a. The term r is the common ratio, and a is the first term of the series. As an example the geometric series given in the introduction,

${\displaystyle {\frac {1}{2}}\,+\,{\frac {1}{4}}\,+\,{\frac {1}{8}}\,+\,{\frac {1}{16}}\,+\,\cdots }$

may simply be written as

${\displaystyle a+ar+ar^{2}+ar^{3}+\cdots }$ , with ${\displaystyle a={\frac {1}{2}}}$ and ${\displaystyle r={\frac {1}{2}}}$.

The following table shows several geometric series with different start terms and common ratios:

Start term, a	Common ratio, r	Example series
4	10	4 + 40 + 400 + 4000 + 40,000 + ···
9	1/3	9 + 3 + 1 + 1/3 + 1/9 + ···
7	1/10	7 + 0.7 + 0.07 + 0.007 + 0.0007 + ···
3	1	3 + 3 + 3 + 3 + 3 + ···
1	−1/2	1 − 1/2 + 1/4 − 1/8 + 1/16 − 1/32 + ···
3	–1	3 − 3 + 3 − 3 + 3 − ···

The behavior of the terms depends on the common ratio r:

If r is between −1 and +1, the terms of the series approach zero in the limit (becoming smaller and smaller in magnitude), and the series converges to a sum. In the case above, where r is 1/2, the series converges to 1.

If r is greater than one or less than minus one the terms of the series become larger and larger in magnitude. The sum of the terms also gets larger and larger, and the series has no sum. (The series diverges.)

If r is equal to one, all of the terms of the series are the same. The series diverges.

If r is minus one the terms take two values alternately (e.g. 2, −2, 2, −2, 2,... ). The sum of the terms oscillates between two values (e.g. 2, 0, 2, 0, 2,... ). This is a different type of divergence and again the series has no sum. See for example Grandi's series: 1 − 1 + 1 − 1 + ···.

Sum[edit]

The sum of a geometric series is finite as long as the absolute value of the ratio is less than 1; as the numbers near zero, they become insignificantly small, allowing a sum to be calculated despite the series containing infinitely many terms. The sum can be computed using the self-similarity of the series.

Example[edit]

Visual derivation of the sum of infinite terms of a geometric series

Consider the sum of the following geometric series:

${\displaystyle s\;=\;1\,+\,{\frac {2}{3}}\,+\,{\frac {4}{9}}\,+\,{\frac {8}{27}}\,+\,\cdots .}$

This series has common ratio 2/3. If we multiply through by this common ratio, then the initial 1 becomes a 2/3, the 2/3 becomes a 4/9, and so on:

${\displaystyle {\frac {2}{3}}s\;=\;{\frac {2}{3}}\,+\,{\frac {4}{9}}\,+\,{\frac {8}{27}}\,+\,{\frac {16}{81}}\,+\,\cdots .}$

This new series is the same as the original, except that the first term is missing. Subtracting the new series (2/3)s from the original series s cancels every term in the original but the first,

${\displaystyle s\,-\,{\frac {2}{3}}s\;=\;1,\;\;\;{\mbox{so }}s=3.}$

A similar technique can be used to evaluate any self-similar expression.

Formula[edit]

For ${\displaystyle r\neq 1}$, the sum of the first n terms of a geometric series is

${\displaystyle a+ar+ar^{2}+ar^{3}+\cdots +ar^{n-1}=\sum _{k=0}^{n-1}ar^{k}=a\left({\frac {1-r^{n}}{1-r}}\right),}$

where a is the first term of the series, and r is the common ratio. We can derive this formula as follows:

${\displaystyle {\begin{aligned}s&=a+ar+ar^{2}+ar^{3}+\cdots +ar^{n-1},\\rs&=ar+ar^{2}+ar^{3}+ar^{4}+\cdots +ar^{n},\\s-rs&=a-ar^{n},\\s(1-r)&=a(1-r^{n}),\end{aligned}}}$

so,

${\displaystyle s=a\left({\frac {1-r^{n}}{1-r}}\right)\quad {\text{(if }}r\neq 1{\text{)}}.}$

As n goes to infinity, the absolute value of r must be less than one for the series to converge. The sum then becomes

${\displaystyle a+ar+ar^{2}+ar^{3}+ar^{4}+\cdots =\sum _{k=0}^{\infty }ar^{k}={\frac {a}{1-r}},{\text{ for }}|r|<1.}$

When a = 1, this can be simplified to

${\displaystyle 1\,+\,r\,+\,r^{2}\,+\,r^{3}\,+\,\cdots \;=\;{\frac {1}{1-r}},}$

the left-hand side being a geometric series with common ratio r.

The formula also holds for complex r, with the corresponding restriction, the modulus of r is strictly less than one.

Proof of convergence[edit]

We can prove that the geometric series converges using the sum formula for a geometric progression:

${\displaystyle {\begin{aligned}1+r+r^{2}+r^{3}+\cdots \ &=\lim _{n\rightarrow \infty }\left(1+r+r^{2}+\cdots +r^{n}\right)\\&=\lim _{n\rightarrow \infty }{\frac {1-r^{n+1}}{1-r}}.\end{aligned}}}$

Since (1 + r + r² + ... + rⁿ)(1−r) = 1−rⁿ⁺¹ and rⁿ⁺¹ → 0 for | r | < 1.

Convergence of geometric series can also be demonstrated by rewriting the series as an equivalent telescoping series. Consider the function,

${\displaystyle g(K)={\frac {r^{K}}{1-r}}.}$

Note that

${\displaystyle 1=g(0)-g(1)\ ,\ r=g(1)-g(2)\ ,\ r^{2}=g(2)-g(3)\ ,\ldots }$

Thus,

${\displaystyle S=1+r+r^{2}+r^{3}+\cdots =(g(0)-g(1))+(g(1)-g(2))+(g(2)-g(3))+\cdots .}$

If

${\displaystyle |r|<1}$

then

${\displaystyle g(K)\longrightarrow 0{\text{ as }}K\to \infty .}$

So S converges to

${\displaystyle g(0)={\frac {1}{1-r}}.}$

Applications[edit]

Repeating decimals[edit]

Main article: Repeating decimal

A repeating decimal can be thought of as a geometric series whose common ratio is a power of 1/10. For example:

${\displaystyle 0.7777\ldots \;=\;{\frac {7}{10}}\,+\,{\frac {7}{100}}\,+\,{\frac {7}{1000}}\,+\,{\frac {7}{10000}}\,+\,\cdots .}$

The formula for the sum of a geometric series can be used to convert the decimal to a fraction,

${\displaystyle 0.7777\ldots \;=\;{\frac {a}{1-r}}\;=\;{\frac {7/10}{1-1/10}}\;=\;{\frac {7/10}{9/10}}\;=\;{\frac {7}{9}}.}$

The formula works not only for a single repeating figure, but also for a repeating group of figures. For example:

${\displaystyle 0.123412341234\ldots \;=\;{\frac {a}{1-r}}\;=\;{\frac {1234/10000}{1-1/10000}}\;=\;{\frac {1234/10000}{9999/10000}}\;=\;{\frac {1234}{9999}}.}$

Note that every series of repeating consecutive decimals can be conveniently simplified with the following:

${\displaystyle 0.09090909\ldots \;=\;{\frac {09}{99}}\;=\;{\frac {1}{11}}.}$

${\displaystyle 0.143814381438\ldots \;=\;{\frac {1438}{9999}}.}$

${\displaystyle 0.9999\ldots \;=\;{\frac {9}{9}}\;=\;1.}$

That is, a repeating decimal with repeat length n is equal to the quotient of the repeating part (as an integer) and 10ⁿ - 1.

Archimedes' quadrature of the parabola[edit]

Archimedes' dissection of a parabolic segment into infinitely many triangles

Main article: The Quadrature of the Parabola

Archimedes used the sum of a geometric series to compute the area enclosed by a parabola and a straight line. His method was to dissect the area into an infinite number of triangles.

Archimedes' Theorem states that the total area under the parabola is 4/3 of the area of the blue triangle.

Archimedes determined that each green triangle has 1/8 the area of the blue triangle, each yellow triangle has 1/8 the area of a green triangle, and so forth.

Assuming that the blue triangle has area 1, the total area is an infinite sum:

${\displaystyle 1\,+\,2\left({\frac {1}{8}}\right)\,+\,4\left({\frac {1}{8}}\right)^{2}\,+\,8\left({\frac {1}{8}}\right)^{3}\,+\,\cdots .}$

The first term represents the area of the blue triangle, the second term the areas of the two green triangles, the third term the areas of the four yellow triangles, and so on. Simplifying the fractions gives

${\displaystyle 1\,+\,{\frac {1}{4}}\,+\,{\frac {1}{16}}\,+\,{\frac {1}{64}}\,+\,\cdots .}$

This is a geometric series with common ratio 1/4 and the fractional part is equal to

${\displaystyle \sum _{n=0}^{\infty }4^{-n}=1+4^{-1}+4^{-2}+4^{-3}+\cdots ={4 \over 3}.}$

The sum is

${\displaystyle {\frac {1}{1-r}}\;=\;{\frac {1}{1-{\frac {1}{4}}}}\;=\;{\frac {4}{3}}.}$

This computation uses the method of exhaustion, an early version of integration. Using calculus, the same area could be found by a definite integral.

Fractal geometry[edit]

The interior of the Koch snowflake is a union of infinitely many triangles.

In the study of fractals, geometric series often arise as the perimeter, area, or volume of a self-similar figure.

For example, the area inside the Koch snowflake can be described as the union of infinitely many equilateral triangles (see figure). Each side of the green triangle is exactly 1/3 the size of a side of the large blue triangle, and therefore has exactly 1/9 the area. Similarly, each yellow triangle has 1/9 the area of a green triangle, and so forth. Taking the blue triangle as a unit of area, the total area of the snowflake is

${\displaystyle 1\,+\,3\left({\frac {1}{9}}\right)\,+\,12\left({\frac {1}{9}}\right)^{2}\,+\,48\left({\frac {1}{9}}\right)^{3}\,+\,\cdots .}$

The first term of this series represents the area of the blue triangle, the second term the total area of the three green triangles, the third term the total area of the twelve yellow triangles, and so forth. Excluding the initial 1, this series is geometric with constant ratio r = 4/9. The first term of the geometric series is a = 3(1/9) = 1/3, so the sum is

${\displaystyle 1\,+\,{\frac {a}{1-r}}\;=\;1\,+\,{\frac {\frac {1}{3}}{1-{\frac {4}{9}}}}\;=\;{\frac {8}{5}}.}$

Thus the Koch snowflake has 8/5 of the area of the base triangle.

Zeno's paradoxes[edit]

Main article: Zeno's paradoxes

The convergence of a geometric series reveals that a sum involving an infinite number of summands can indeed be finite, and so allows one to resolve many of Zeno's paradoxes. For example, Zeno's dichotomy paradox maintains that movement is impossible, as one can divide any finite path into an infinite number of steps wherein each step is taken to be half the remaining distance. Zeno's mistake is in the assumption that the sum of an infinite number of finite steps cannot be finite. This is of course not true, as evidenced by the convergence of the geometric series with ${\displaystyle r=1/2}$.

Euclid[edit]

Book IX, Proposition 35^[1] of Euclid's Elements expresses the partial sum of a geometric series in terms of members of the series. It is equivalent to the modern formula.

Wikipedia