필즈상 수상자도 도전한 무작위 베르누이 행렬 문제

1과 -1로 이뤄진 n차원 벡터 n개를 무작위로 뽑았습니다. 이 n개와 원점이 n-1차원 공간에 있을 확률은 얼마일까요? 최근 50년 이상 미해결이었던 이 문제를 풀었다고 주장한 논문이 인터넷에 공개됐습니다.

동전을 던져서 앞면이 나오면 1, 뒷면이 나오면 -1이라고 적어봅시다. 이걸 n번 반복하면 1 또는 -1로 총 n개의 수를 얻게 됩니다.이 수들을 묶어서 n차원 ‘벡터’, 즉 n개의 수를 순서쌍으로 나타냅니다. 예를 들어 n=3이면, 즉 동전 던지기를 3번 반복하면 아래 8가지 경우가 나올 수 있고, 각각이 나올 확률은 입니다. 이 벡터들이 나타내는 점을 3차원 좌표 공간에 그리면 정육면체의 꼭짓점 8개가 됩니다.

이제 주사위를 3번 던져서 3차원 벡터를 고르는 작업을 3번 반복해 봅니다. 정육면체의 꼭짓점 8개 중 하나를 뽑는 작업을 세 번 하는 것입니다. 

이렇게 뽑은 3차원의 세 점과 원점이 2차원 평면에 있을 확률은 얼마일까요 

만약 (1, -1, -1), (-1, 1, -1), (-1, -1, 1) 이렇게 3개를 뽑았다면 절대 원점과 이 세 점이 한 평면에 있을 수 없습니다. 하지만 같은 벡터가 2번 나오면 원점과 같은 평면에 있는 게 가능합니다. 또 앞선 두 차례에서 (1, 1, 1), (-1, -1, -1)을 뽑았다면 나머지 한 점을 어떻게 뽑더라도 그 4개 점을 동시에 지나는 평면이 있습니다. 원점과 (1, 1, 1), (-1, -1, -1)은 한 직선 위에 있는데, 직선 1개와 점 1개를 지나는 평면은 항상 있습니다.

이제 확률을 계산해보겠습니다. 정육면체 꼭짓점은 서로 대칭성이 있으니 처음에 뽑은 1개 점을 고정하면 나머지 2점이 어디 있는지만 알아내면 됩니다. 처음 뽑은 점이 (1, 1, 1)이라고 가정해봅시다. 그러면 나머지 둘 중 적어도 하나가 (1, 1, 1)이거나 (-1, -1, -1)이면 원점과 같은 평면에 있는데, 이럴 확률은 1-( X ), 즉 입니다. 

원점과 (1, 1, 1)을 지나는 직선을 포함하는 평면이 정육면체의 (1, 1, 1), (-1, -1, -1) 아닌 6개 꼭짓점 중 하나 이상을 지나는 경우도 살펴봐야 합니다. 이런 평면은 총 3개가 있습니다. 주사위에서 마주 보는 면에 있는 두 꼭짓점을 잡고 회전시켜보면서 생각해보면 쉽습니다. 3개 각각에 (1, 1, 1), (-1, -1, -1) 아닌 꼭짓점이 2개씩 들어있어 3××=이 됩니다. 따라서 n이 3일 때 확률은 두 확률을 합한 = 입니다. 이 문제를 n차원으로 확장하면 어떻게 될까요?

필즈상 수상자들도 도전한 문제

이 문제는 지난 50년 이상 수학자들이 고민해왔던 문제 중 하나였습니다. 1960년대에 헝가리 출신 수학자 야노시 콤로시가 이 문제의 확률인 은 n이 커지면 0으로 수렴한다는 것을 처음 증명했습니다. 하지만 얼마나 0에 빠르게 가까워지는지는 알지 못했습니다. 이후 1970년대에 ≤이라는 부등식이 충분히 큰 C에 대해 성립한다는 것이 증명돼 그나마 보다는 빠르게 0으로 수렴한다는 것을 알게 됐지만, 그것 역시 충분히 빠른 것은 아니었습니다.

생각해보면 첫 번째 벡터와 두 번째 벡터를 똑같게 뽑을 확률이 벌써 입니다. 이렇게 두 벡터가 같다면 나머지 n-2개 벡터가 어떻든 n-1차원 부분 공간에 들어가게 됩니다. 따라서 ≥임을 알 수 있습니다. 

한참 후인 1995년 콤로시와 미국 수학자 제프 칸, 2012년 아벨상을 받은 헝가리 수학자 세메레디 엔드레 이렇게 세 명의 수학자가 ≤0.999ⁿ을 증명합니다. n이 커지면 0.999ⁿ은 0.999가 1보다 작으므로 결국은 보다는 빠른 속도로 0에 수렴합니다. 하지만 0.999는 그리 만족스럽지 않은 값이었습니다. 과 0.999ⁿ은 엄청나게 차이가 납니다.

2006년 베트남 수학자 반 부와 그해 필즈상을 받은 호주 수학자 테린스 타오가 0.999를 0.939로 낮추는 데 성공합니다. 두 수학자는 1년 후 n이 충분히 크면 0.750001ⁿ보다 작다는 것도 증명했지요. 사실 타오는 수학계의 모차르트라고 불리는 유명한 수학자입니다. 부는 베트남 출신이지만 대학 학부부터 헝가리로 유학을 하러 가서 수학을 공부했습니다. 학부를 졸업했을 당시 헝가리의 유명한 수학자인 로바스 라슬로가 헝가리에서 미국 예일대로 자리를 옮겼는데, 그때 그를 따라 예일대로 유학을 갔습니다. 로바스의 밑에서 공부하며 박사학위를 받았습니다. 지금 부는 예일대 교수입니다.

2010년 프랑스 수학자 장 부르갱과 부, 부의 지도 학생 필립 우드 이렇게 3명은 0.70711ⁿ으로 낮추는 데 성공합니다. 참고로 부르갱은 1994년 필즈상을 받은 프랑스 수학자인데, 안타깝게도 2018년 12월 22일에 만 64세의 나이로 별세했습니다.

장 부르갱은 실해석학 분야의 저명한 수학자로 1994년 필즈상을 받았다. 2017년에는 브레이크스루 수학상을 받기도 했다. 하지만 2018년 12월 췌장암을 이기지 못하고 세상을 떠났다. Bruno FahyBelga

50년 난제 풀린 걸까? 

그러던 2018년 12월 21일, 인터넷 논문 공개사이트인 아카이브에 2010년 결과보다 훨씬 좋은 결과를 담은 논문이 올라왔습니다. 미국 조지아공대 수학과 교수인 러시아 출신의 콘스탄틴 티호미로프가 0.50001ⁿ으로 값을 크게 낮춘 것입니다. 더 정확하게 표현하면 ε을 아무리 작은 양수로 하더라도 n이 충분히 크면 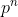≤(0.5+ε)ⁿ이 된다는 것을 증명합니다. 

아직 검증을 기다려야겠지만 이 논문 결과가 옳다면 이제야 이 과 거의 같은 속도로 0으로 수렴한다는 것을 알게 된 것입니다. 오랜 미해결 문제가 하나 풀린 셈이 되지요.

좀 더 센 추측으로 n이 충분히 크면 p≤(1+ε)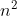 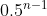이라는 추측도 있습니다. 이는 아직 미해결인데, 만일 옳다면 매우 정밀한 부등식이 될 것입니다. 우변이 대략 어떤 두 벡터가 서로 같거나 아니면 완전히 부호가 반대일 확률과 가깝기 때문입니다. 이렇게 정밀한 추측도 언젠가는 수학자들이 해결할 수 있는 영역에 들어오겠죠? 

러시아 수학자 콘스탄틴 티호미로프. Georgia institute of Technology

동아사이언스