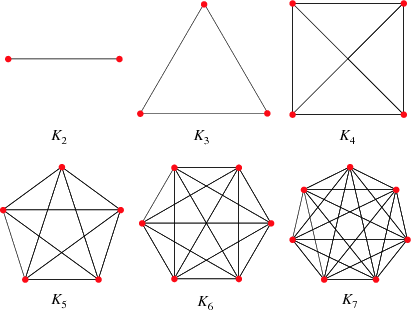
A complete graph is a graph in which each pair of graph vertices is connected by an edge. The complete graph with 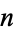 graph vertices is denoted
graph vertices is denoted 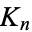 and has
and has 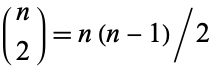 (the triangular numbers) undirected edges, where
(the triangular numbers) undirected edges, where 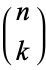 is a binomial coefficient. In older literature, complete graphs are sometimes called universal graphs.
is a binomial coefficient. In older literature, complete graphs are sometimes called universal graphs.
The complete graph on 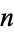 nodes is implemented in the Wolfram Language as CompleteGraph[n]. Precomputed properties are available using GraphData[
nodes is implemented in the Wolfram Language as CompleteGraph[n]. Precomputed properties are available using GraphData[ "Complete", n
"Complete", n ]. A graph may be tested to see if it is complete in the Wolfram Language using the function CompleteGraphQ[g].
]. A graph may be tested to see if it is complete in the Wolfram Language using the function CompleteGraphQ[g].
The complete graph on 0 nodes is a trivial graph known as the null graph, while the complete graph on 1 node is a trivial graph known as the singleton graph.
In the 1890s, Walecki showed that complete graphs 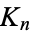 admit a Hamilton decomposition for odd
admit a Hamilton decomposition for odd 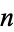 , and decompositions into Hamiltonian cycles plus a perfect matching for even
, and decompositions into Hamiltonian cycles plus a perfect matching for even 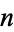 (Lucas 1892, Bryant 2007, Alspach 2008). Alspach et al. (1990) give a construction for Hamilton decompositions of all
(Lucas 1892, Bryant 2007, Alspach 2008). Alspach et al. (1990) give a construction for Hamilton decompositions of all 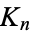 .
.
The graph complement of the complete graph 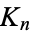 is the empty graph on
is the empty graph on 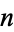 nodes.
nodes. 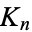 has graph genus
has graph genus ![[(n-3)(n-4)/12]](http://mathworld.wolfram.com/images/equations/CompleteGraph/Inline17.gif) for
for 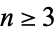 (Ringel and Youngs 1968; Harary 1994, p. 118), where
(Ringel and Youngs 1968; Harary 1994, p. 118), where ![[x]](http://mathworld.wolfram.com/images/equations/CompleteGraph/Inline19.gif) is the ceiling function.
is the ceiling function.
The adjacency matrix 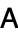 of the complete graph
of the complete graph 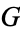 takes the particularly simple form of all 1s with 0s on the diagonal, i.e., the unit matrix minus the identity matrix,
takes the particularly simple form of all 1s with 0s on the diagonal, i.e., the unit matrix minus the identity matrix,
(1)
|


The chromatic polynomial 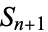 of
of 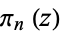 is given by the falling factorial
is given by the falling factorial 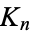 . The independence polynomial is given by
. The independence polynomial is given by
(2)
|
and the matching polynomial by
(3)
| |||
(4)
|
The chromatic number and clique number of 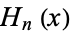 are
are 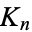 . The automorphism group of the complete graph
. The automorphism group of the complete graph 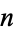 is the symmetric group
is the symmetric group 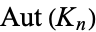 (Holton and Sheehan 1993, p. 27). The numbers of graph cycles in the complete graph
(Holton and Sheehan 1993, p. 27). The numbers of graph cycles in the complete graph 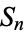 for
for 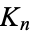 , 4, ... are 1, 7, 37, 197, 1172, 8018 ... (OEIS A002807). These numbers are given analytically by
, 4, ... are 1, 7, 37, 197, 1172, 8018 ... (OEIS A002807). These numbers are given analytically by
(5)
| |||
(6)
|
where 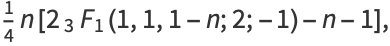 is a binomial coefficient and
is a binomial coefficient and 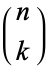 is a generalized hypergeometric function (Char 1968, Holroyd and Wingate 1985).
is a generalized hypergeometric function (Char 1968, Holroyd and Wingate 1985).
It is not known in general if a set of trees with 1, 2, ..., 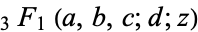 graph edges can always be packed into
graph edges can always be packed into 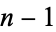 . However, if the choice of trees is restricted to either the path or star from each family, then the packing can always be done (Zaks and Liu 1977, Honsberger 1985).
. However, if the choice of trees is restricted to either the path or star from each family, then the packing can always be done (Zaks and Liu 1977, Honsberger 1985).
댓글 없음:
댓글 쓰기