로켓이 발사되는 순간, 폭탄이 터지는 순간, 어머니의 경고가 시작되는 순간. 수는 거꾸로 흐르기 시작합니다.
3,2,1,0
여기에는 물건의 개수를 셀 때와는 다른 수가 들어있습니다. 0입니다. 중요한 사건 전에는 늘 0이 있었습니다. 그러나
이 수는 다른 수들이 탄생하고도 수 만년이 지나서야 발명되었습니다.
수의 탄생
1937년 체코슬로바키아 고대 유적지. 고고학자 카를 압솔롬은 발굴도중 10cm가량 되는 늑대뼈를 발견합니다. 여기에는 55개의 작은 눈금들이 5개 단위로 새겨져
있었습니다. 이 늑대뼈는 수에 대한 기록입니다.
2만 년 전의 원시인들은 뼈에 눈금을 그어 진짜 사물과 일대일로 비교했습니다. 그러다보면 사물이 본래보다 부족한지
많은지 알 수 있었죠. 5개 단위로 눈금을 그은 까닭은 손가락이 5개이기 때문입니다. 셈을 하기 위해서는 보통 손가락과 발가락을 사용해야했죠.
그래서 5개 단위로 묶어세기(fiving)는 여러 문화권에서 찾아볼 수 있습니다.
이것은 순전히 임의적인 결정이었습니다. 만약에 손가락이 6개였다면 묶어 세기의 단위는 5가 아니라 6이 되었겠죠.
바빌로니아인들이 수를 세는 방법
오늘날의 이라크에 해당하는 바빌로니아 지역 사람들은 60진법을 사용했습니다. 문명의 발생지이자 고대수학의 중심지였던
바빌로니아는 가장 훌륭한 수 체계를 가지고 있었습니다. 바빌로니아에서는 단 2개의 기호로 모든 수를 나타낼 수 있었죠. 그들이 단 2개의 기호로
눈부신 수학의 발전을 이룩할 수 있었던 이유는 '위치 값(Place value)'과 '플레이스 홀더(place holder)'를 사용했기
때문입니다. 위치 값과 플레이스 홀더만 사용한다면 그 어떤 큰 수라도 나타낼 수 있죠.
‘위치 값’이란 위치에 따라 그 수의 값이 달라짐을 의미합니다. 203의 2와 23의 2는 서로 의미하는 바가
다릅니다. 203의 2는 200을 23의 2는 20을 나타내죠. ‘플레이스 홀더’는 203과 23을 구분해주는 0과 같은 기호를 의미합니다.
고대 중국에서는 산가지를 놓을 때 2와 3사이에 빈칸을 두거나 획의 방향을 다르게 하는 식으로 203을 표현했고, 바빌로니아에서는 쐐기를
비스듬하게 찍음으로써 2와 3사이에 플레이스 홀더를 마련했습니다. 오늘날 우리가 수에서 사용하는 플레이스 홀더는 0이죠.
이때 0은 수(numbers)가 아닙니다. 203과 23을
구별하기 위한 기호(digit)일 뿐이죠. 아무것도 없음을 나타내는 0이라는 수가
탄생하기까지는 오랜 시간이 필요했습니다. 사과가 3개 있을 때 우리는 “사과가 3개 있어”라고 말할 수 있습니다. 그러나 사과가 없을 때
“사과가 0개 있어”라고 말하기는 힘들죠. 그냥 “사과가 없어”라고 말하면 되니까요. 0은 필요하지 않았고, 0 없이도 인류문명은 눈부신 발전을
이룩했습니다. 수많은 문화권에서 수많은 언어로 수를 셌지만 없음을 세는 수는 없었습니다.
그리스의 우주를 파괴한 수 0
고대의 수학자는 철학자이기도 했습니다. ‘숫자 사이에 있는 기호 0’의 의미에 대해 고민하다 보면 ‘없음을 나타내는
수 0’에 대해 생각할 수도 있죠. 그러나 0은 있어도 그만, 없어도 그만인 수가 아니었습니다. 고대 그리스인들에게 0은 존재해서는 안 되는
수였습니다.
그들은 0을 혐오했고 두려워했습니다. 0은 공허였습니다. 그리스인들은 공허와 혼돈에서 우주가 탄생했다고 믿었고,
언젠가는 공허와 혼돈이 우주를 원초적인 상태로 되돌릴 것이라고 여겼습니다. 따라서 0은 세상의 종말을 의미했습니다.
밤하늘에 사로잡힌 그리스 천문학자들은 바빌로니아의 60진법이 천문학에 필요한 복잡한 계산에 효과적이라는 것을
알았습니다. 그들은 바빌로니아의 60진법을 이용해 하늘을 계산합니다. 그러나 거기까지였습니다. 계산이 끝나면 결과 값을 0이 없는 그리스식의
숫자로 바꾸어버렸습니다. 0은 그 정도로 가까이 하고 싶지 않은 존재였습니다. 아리스토텔레스의 우주관을 받아들인 천문학자들은 더욱
그러했겠죠.
아리스토텔레스의 우주관은 무한과 진공을 거부했습니다. 0은 진공, 빈 공간과 같은 의미였습니다. 존재할 수 없는
것이니 나타내서도 안 되는 것이었죠. 따라서 그들은 플레이스 홀더로서의 0도 받아들이지 않습니다. 중세 기독교 사회에서 아리스토텔레스의 우주관을
거부하는 것은 곧 신을 거부하는 것이었습니다.
신의 수 0
BC4세기, 인도에 알렉산더왕의 군대가 도착합니다.
바빌로니아의 수 체계는 이 침략을 통해 인도에 전해졌습니다. 플레이스 홀더로서의 0도 이때 전해졌죠. 인도인들에게는 무를 거부해야할 이유가
없었으니 인도의 기수법은 곧 바빌로니아 식으로 바뀌게 됩니다. 인도의 수학자들은 바빌로니아아의 60진법을 자신들이 사용하던 10진법으로 변형해
사용했습니다. 그들은 새로운 기수법을 통해 주판을 사용하지 않고도 빠르게 사칙연산을 할 수 있었죠.
인도의 수학자와 철학자들은 자리기호로서의 0을 다른 눈으로 바라보기 시작했습니다. 그 안에서 신의 모습을 발견한
것입니다. 서양에서는 우주관과 종교 때문에 0을 거부했지만 인도에서는 우주관과 종교 때문에 0을 적극적으로 포용했습니다.
무(無)는 힌두교에서 중요하게 여기는 개념입니다. 힌두교의
우주는 창조와 파괴가 한데 뒤섞여 무한히 펼쳐집니다. 그 우주는 무에서 탄생했습니다. 인도인들은 우주의 근원인 무를 두려워하지 않았습니다.
힌두교 최고의 신이자, 우주를 창조한 시바(Shiva)는 궁극의 무였죠. 인도인들은
신과 가까워지기 위해 무를 추구했습니다.
"1/0에 어떤 수를 더하든 빼든 아무런 변화도 없다. 영원불멸한 무한한 신에게 어떤 변화가 없는 것과 마찬가지이다." - 바스카라 (Bhaskara AD1114-1185)
악마라 불린 교황
프랑스 오리야크 수도원의 학생, 제르베르(946-1003)는 스페인에서 수학과 아라비아 학문을 배웠습니다. 당시
스페인의 번역가들은 아라비아 서적을 번역하는데 열을 올렸는데, 그 중에는 인도-아라비아 숫자에 관한 내용도 있었습니다. 제르베르는 이 새로운
숫자의 가치를 알아보았습니다. 그는 훗날 교황이 되어 실베스테르 2세라는 이름으로 살게 되죠.
중세 서양에서는 기독교 수도승만이 수학을 공부했습니다. 기도 시간과 교회를 운영할 돈을 관리하기 위해서였죠. 그들은
이를 위해 주판(셈판 counting board)을 사용했습니다.
제르베르는 아라비아 수를 이용해 주판을 개량합니다. 우선 사용하는 돌의 개수를 줄이기 위해 아라비아수가 쓰인 돌을
이용했습니다. 제르베르의 주판 계산법은 창의적이고 유용했지만 로마숫자와 로마의 수 체계에 익숙한 수도승들은 이를 받아들이기 힘들어했죠.
제르베르의 주판을 가장 잘 활용할 수 있는 이는 제르베르 자신이었습니다.
제르베르는 주판을 이용해 매우 빠른 계산을 선보였습니다. 이 때문에 악마와 계약했다는 풍설에 평생을 시달립니다.
1648년 교황청에서는 악마들이 아직도 제르베르와 함께 있는지 확인하기 위해 그의 무덤을 파헤쳐야 한다고 주장하기도 했습니다. 만약 제르베르가
0의 사용을 주장했다면 정말로 그렇게 했을지도 모릅니다. 다행히도 제르베르의 인도-아라비아 수에는 0이 포함되어 있지 않았습니다.
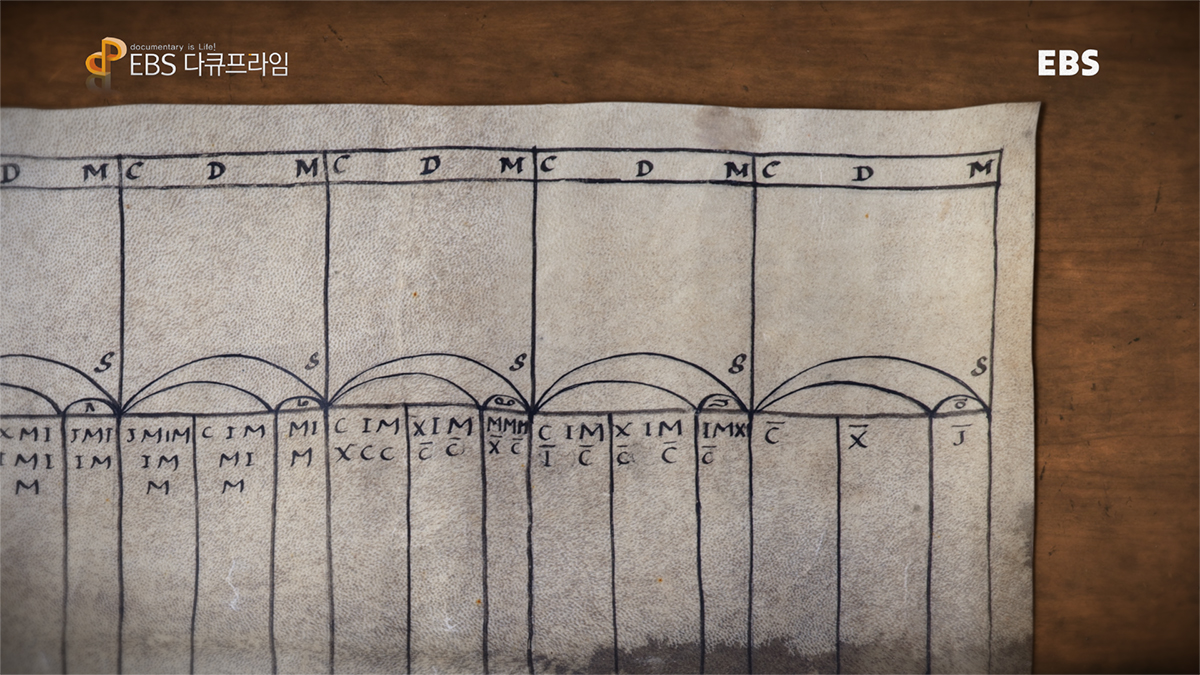
이탈리아 상인의 결정, 주판파 VS 산술파
15세기 이탈리아 상인들은 오늘날의 부모들과 비슷한 고민에 빠졌습니다. 자식의 교육문제입니다. 자식들을 훌륭한
상인으로 키우기 위해서는 수학교육이 매우 중요했습니다. 당시에는 주판계산과 인도-아라비아 수를 이용한 필산계산이 공존했습니다. 주판을 이용하는
이들은 주로 성직자들이었고, 필산을 이용하는 이들은 상인과 은행가였죠. 이들은 각각 주판가(abacist)와 필산가(algorist)로 불렸습니다. 주판계산을 가르치는 학교와 필산계산을 가르치는 학교도 따로
있었습니다. 둘은 경쟁관계였죠.
주판파와 필산파는 누구의 계산이 우월한지 가리기 위한 대결을 벌이고는 했습니다. 많은 경우 주판파가 승리했죠. 주판을
놓는 법이 필산보다 어렵긴 하지만, 숙달된 주판가는 수를 매우 빠르게 다룰 수 있었습니다. 문제를 듣자마자 답을 말하기도 했죠.
그러나 역사는 필산파의 손을 들어주었습니다. 필산은 무리수, 소수점 계산에 강점을 보입니다. 주판보다 정확하고 빠른
계산이 가능했죠. 르네상스의 수학은 점점 복잡한 계산을 요구했기에 수학자들은 주판을 버리고 새로운 숫자를 이용하기 시작합니다.
필산이 살아남은 또 다른 이유는 쉽기 때문입니다. 필산은 사람들에게 자유를 주었습니다.
1,2,3,4,5,6,7,8,9 그리고 0. 이 숫자들을 이용하면 누구나 사칙연산을 할 수 있습니다. 이제 사람들은 계산을 위해 주판가의 대문을
두드릴 필요가 없게 되었습니다.
“이 심오하고도 중대한 개념은 너무 단순해 보여 그것의 진정한 장점을 간과하기 쉽다. 하지만 모든 계산을 쉽게 해주는 바로 그 단순성과 편리함 덕분에 산술은 가장 탁월하고 유용한 발명의 반열에 오르게 되었다.” -피에르-시몽 라플라스(Pierre-Simon Laplace)
EBS 다큐프라임




댓글 없음:
댓글 쓰기