위성 중계 TV를 볼 수 있게 해 주는 파라볼라 안테나는 포물선 여러 개가 포개져 있는 모양이다. ‘접시 안테나’라고도 부르는 이 안테나는 왜 포물선 모양을 하고 있을까? 이차함수 그래프에서 그 답을 찾아보자.
방송 신호의 증폭은 초점에서
전파를 주고받는 안테나는 위성 통신을 가능하게 해 준다. 우리가 집에 앉아 지구 반대편에서 일어나는 일을 TV로 시청할 수 있는 것도 바로 안테나 덕분이다. 안테나는 곤충의 ‘더듬이’를 의미하는 말로, 전파를 잡는 역할을 한다는 데서 이런 이름이 붙었다. 위성은 지구국이 송신한 신호를 수신해 이를 다른 지구국으로 보내거나 다른 위성에 중계한다.
신호를 보낼 때는 정확히 한 방향으로 보내야 전파도 약해지지 않고 간섭도 일어나지 않아 멀리까지 도달할 수 있다. 위성 통신의 경우 ‘전리층’을 통과해야 한다. 태양 에너지에 의해 공기 분자가 이온화돼 자유전자가 밀집해 있는 곳이 전리층이다. 전리층은 지상에서 보낸 전파를 흡수하거나 반사하기 때문에 무선 통신에 큰 영향을 미친다. 이때 주파수가 높을수록 전리층을 잘 통과한다. 그래서 위성 통신에서는 1GHz(기가헤르츠) 이상으로 높은 마이크로파를 사용한다.
지상에서 신호를 주고받을 때도 마찬가지다. 송신국과 수신국 사이가 너무 멀거나 중간에 장애물이 많으면 전파가 약해진다. 이럴 때는 여러 방향에서 오는 전파를 한 점에 모아 증폭시키면 전파의 세기를 높일 수 있다.
신호를 보낼 때는 정확히 한 방향으로 보내야 전파도 약해지지 않고 간섭도 일어나지 않아 멀리까지 도달할 수 있다. 위성 통신의 경우 ‘전리층’을 통과해야 한다. 태양 에너지에 의해 공기 분자가 이온화돼 자유전자가 밀집해 있는 곳이 전리층이다. 전리층은 지상에서 보낸 전파를 흡수하거나 반사하기 때문에 무선 통신에 큰 영향을 미친다. 이때 주파수가 높을수록 전리층을 잘 통과한다. 그래서 위성 통신에서는 1GHz(기가헤르츠) 이상으로 높은 마이크로파를 사용한다.
지상에서 신호를 주고받을 때도 마찬가지다. 송신국과 수신국 사이가 너무 멀거나 중간에 장애물이 많으면 전파가 약해진다. 이럴 때는 여러 방향에서 오는 전파를 한 점에 모아 증폭시키면 전파의 세기를 높일 수 있다.
파라볼라 안테나의 형태가 포물선 모양인 이유도 바로 이 때문이다. 평면이 아닌 곡면으로 이뤄진 안테나의 접시는 여러 방향에서 오는 전파 중 축과 나란히 들어오는 전파를 한 점으로 모아 준다. 이 점을 기하학에서는 포물선의 ‘초점’이라고 한다. 포물선의 초점에 수신기를 설치하면 외부에서 들어오는 작은 신호도 증폭시킬 수 있어 통신의 효율을 높일 수 있다. 단, 접시의 크기가 전파의 파장보다 커야 한다.
생활 주변에서도 안테나와 비슷한 예를 찾아 볼 수 있다. 어두운 길을 밝혀 주는 자동차의 전조등이나 랜턴은 빛이 직선으로 나가야 제 기능을 한다. 자세히 들여다보면 내부가 포물선 모양의 거울로 돼 있다는 것을 알 수 있다. 그래서 이 포물선의 초점에 있는 전구에서 나온 빛이 분산되지 않고 거울에 부딪쳐 축과 평행한 방향으로 뻗어 나간다.
생활 주변에서도 안테나와 비슷한 예를 찾아 볼 수 있다. 어두운 길을 밝혀 주는 자동차의 전조등이나 랜턴은 빛이 직선으로 나가야 제 기능을 한다. 자세히 들여다보면 내부가 포물선 모양의 거울로 돼 있다는 것을 알 수 있다. 그래서 이 포물선의 초점에 있는 전구에서 나온 빛이 분산되지 않고 거울에 부딪쳐 축과 평행한 방향으로 뻗어 나간다.
안테나의 효율을 높이려면?
파라볼라 안테나를 옆에서 바라보면 포물선이다. 수신기를 설치하려면 포물선의 초점을 찾아야 한
다. 이러한 문제는 이차함수 그래프와 그 식을 활용하면 해결할 수 있다.
이차함수 식의 가장 기본적인 형태는 꼭짓점을 원점으로 하는 y=ax2(a≠0)이다. 이때 a= (1/4p)(p≠0)이라 하면 이차함수 식은 y=(1/4p)x2이 된다. 여기서 (0, p)를 우리는 포물선의 초점이라 정의한다.
이 포물선을 좀 더 확장시켜 생각해 보자. 포물선을 x축 방향으로 m만큼, y축 방향으로 n만큼 평행이동시키면 초점의 좌표는 (0, p)에서 (m, p+n)이 되고, 이차함수의 식은 y=ax2에서 y-n=a(x-m)2이 된다. 다시 p값을 대입해 정리하면, y= (1/4p)(x-m)2+n이 된다.
다. 이러한 문제는 이차함수 그래프와 그 식을 활용하면 해결할 수 있다.
이차함수 식의 가장 기본적인 형태는 꼭짓점을 원점으로 하는 y=ax2(a≠0)이다. 이때 a= (1/4p)(p≠0)이라 하면 이차함수 식은 y=(1/4p)x2이 된다. 여기서 (0, p)를 우리는 포물선의 초점이라 정의한다.
이 포물선을 좀 더 확장시켜 생각해 보자. 포물선을 x축 방향으로 m만큼, y축 방향으로 n만큼 평행이동시키면 초점의 좌표는 (0, p)에서 (m, p+n)이 되고, 이차함수의 식은 y=ax2에서 y-n=a(x-m)2이 된다. 다시 p값을 대입해 정리하면, y= (1/4p)(x-m)2+n이 된다.
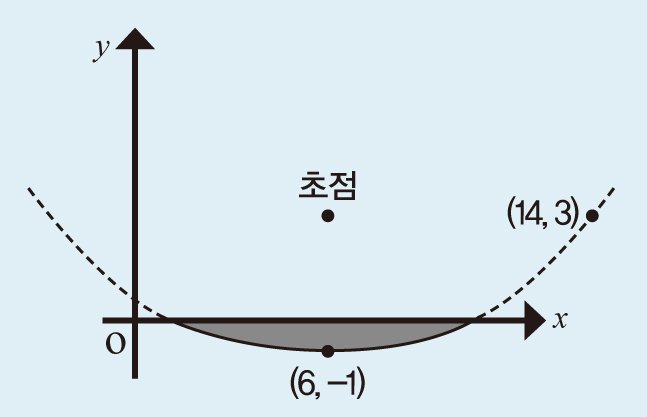
아래 그림과 같이 안테나로 사용하려는 접시를 좌표 평면 위에 놓았다. 이차함수 그래프를 활용해 접시
의 지름과 초점의 좌표를 구해 보자.
의 지름과 초점의 좌표를 구해 보자.
안테나 모양의 포물선은 꼭지점이 (6, -1)이고, 포물선 위의 다른 한 점은 (14, 3)이다. 초점의 좌표를 구하려면, 포물선의 이차함수 식이 필요하다. 표준형인 y=a(x-m)2+n에서 꼭지점은 (m, n)을 나타내므로 이를 대입하면, y=a(x-6)2-1식은 이 된다.
포물선 위에 놓인 점은 이 관계식을 만족하므로, (14, 3)을 대입하면 식이 성립한다. 따라서 a값은
다음과 같이 구할 수 있다.
포물선 위에 놓인 점은 이 관계식을 만족하므로, (14, 3)을 대입하면 식이 성립한다. 따라서 a값은
다음과 같이 구할 수 있다.
3=a(14-6)2-1 ⇒ 3=64a-1,
⇒ 64a=4,
⇒ a= 1/16
a값을 대입하면, 포물선의 이차함수 식은 y=1/16(x-6)2-1이 된다. 이때 a=1/4p(p≠0)에서 p=4이고, m과 n은 각각 6과 -1이란 것을 알 수 있다. 따라서 초점의 좌표 (m, p+n)은 (6, 3)이다.
이번에는 접시의 지름을 구해 보자(단위는 m를 사용한다). x축과 이차함수 그래프가 만나는 두 점 사이의 거리가 안테나 접시의 지름이다. x축은 y=0으로 나타낼 수 있으므로 이차함수 식과 연립하면 이차방정식 (1/16)(x-6)2-1=0을 얻는다. 이를 풀면, 두 근은 2와 10이다. 따라서 x축과 이차함수의 그래프가 만나는
두 점은 (2, 0), (10, 0)이고, 두 점 사이의 거리인 8m가 접시의 지름이다.
⇒ 64a=4,
⇒ a= 1/16
a값을 대입하면, 포물선의 이차함수 식은 y=1/16(x-6)2-1이 된다. 이때 a=1/4p(p≠0)에서 p=4이고, m과 n은 각각 6과 -1이란 것을 알 수 있다. 따라서 초점의 좌표 (m, p+n)은 (6, 3)이다.
이번에는 접시의 지름을 구해 보자(단위는 m를 사용한다). x축과 이차함수 그래프가 만나는 두 점 사이의 거리가 안테나 접시의 지름이다. x축은 y=0으로 나타낼 수 있으므로 이차함수 식과 연립하면 이차방정식 (1/16)(x-6)2-1=0을 얻는다. 이를 풀면, 두 근은 2와 10이다. 따라서 x축과 이차함수의 그래프가 만나는
두 점은 (2, 0), (10, 0)이고, 두 점 사이의 거리인 8m가 접시의 지름이다.
수학동아




댓글 없음:
댓글 쓰기