2012년 12월 28일 금요일

스튜어트 정리( Stewart's theorem)

스튜어트의 정리( Stewart's theorem)는 삼각형을 구성하는 선분들의 길이에 관한 식이다. 스튜어트는 스코틀랜드의 수학자 다.

정리

$a, b, c$ 는 삼각형의 세 변의 길이라고 하고, $d$ 는 변 $a$ 와 그 반대편의 꼭지점을 잇는 선분의 길이라고 하자. $d$ 가 변 $a$ 를 길이 $n$ , $m$ 으로 나눈다고 하면, 다음 관계가 성립한다.

$b^2m + c^2n = a(d^2 + mn)\,$

특히 $m = n$ 일 경우 $d$ 는 중선이 되고 이때 관계식은 중선정리가 된다.

증명

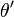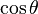$\theta$ 는 $m$ 과 $d$ 가 이루는 각이고, $\theta'$ 는 $n$ 과 $d$ 가 이루는 각이라 하자. 두 각을 합하면 180도 이므로 코사인의 성질 때문에 $\cos \theta' = -\cos \theta$ 이다. 코사인 법칙에 의해 다음 식이 성립한다.

$\begin{align} c^2 &= m^2 + d^2 - 2dm\cos\theta \\ b^2 &= n^2 + d^2 - 2dn\cos\theta' \\ &= n^2 + d^2 + 2dn\cos\theta.\, \end{align}$

첫 번째 식에 $n$ 을 곱하고, 두 번째 식에 $m$ 을 곱하여 더해서 $\cos \theta$ 를 제거하면 다음을 얻는다.

$\begin{align} &b^2m + c^2n \\ &= nm^2 + n^2m + (m+n)d^2 \\ &= (m+n)(mn + d^2) \\ &= a(mn + d^2) \\ \end{align}$

Stewart's Theorem

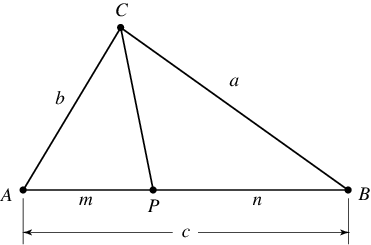
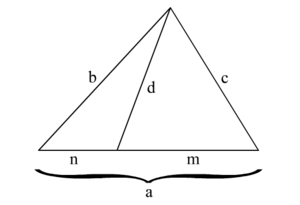
Let a Cevian

be drawn on a triangle

, and denote the lengths

and

, with

. Then Stewart's theorem, also called Apollonius' theorem, states that

In particular, if

is the fraction of the distance of

from vertex

to vertex

and

, then

, and

giving the above identity.
Bottema (1979) extended the formula to simplices in higher dimensions, and Bottema (1980-1981) explicitly considered the tetrahedron.

Wolfram| MathWorld

댓글 없음:

댓글 쓰기