Cube

The cube is the Platonic solid (also called the regular hexahedron). It is composed of six square faces that meet each other at right angles and has eight vertices and 12 edges. It is also the uniform polyhedron and Wenninger model . It is described by the Schläfli symbol and Wythoff symbol .
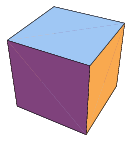
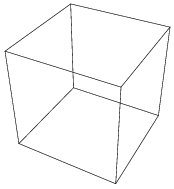
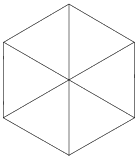
The cube is illustrated above, together with a wireframe version and a net (top figures). The bottom figures show three symmetric projections of the cube.

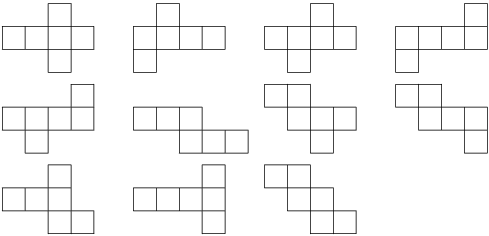
There are a total of 11 distinct nets for the cube (Turney 1984-85, Buekenhout and Parker 1998, Malkevitch), illustrated above, the same number as the octahedron. Questions of polyhedron coloring of the cube can be addressed using the Pólya enumeration theorem.
A cube with unit edge lengths is called a unit cube.
The surface area and volume of a cube with edge length are

			(1)
			(2)

Because the volume of a cube of edge length is given by , a number of the form is called a cubic number (or sometimes simply "a cube"). Similarly, the operation of taking a number to the third power is called cubing.
A unit cube has inradius, midradius, and circumradius of

			(3)
			(4)
			(5)

The cube has a dihedral angle of

(6)

In terms of the inradius of a cube, its surface area and volume are given by

			(7)
			(8)

so the volume, inradius, and surface area are related by

(9)

where is the harmonic parameter (Dorff and Hall 2003, Fjelstad and Ginchev 2003).

The illustration above shows an origami cube constructed from a single sheet of paper (Kasahara and Takahama 1987, pp. 58-59).
Sodium chloride (NaCl; common table salt) naturally forms cubic crystals.

The world's largest cube is the Atomium, a structure built for the 1958 Brussels World's Fair, illustrated above (© 2006 Art Creation (ASBL); Artists Rights Society (ARS), New York; SABAM, Belgium). The Atomium is 334.6 feet high, and the nine spheres at the vertices and center have diameters of 59.0 feet. The distance between the spheres along the edge of the cube is 95.1 feet, and the diameter of the tubes connecting the spheres is 9.8 feet.

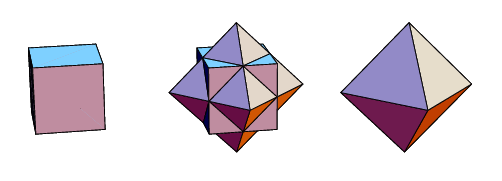
The dual polyhedron of a unit cube is an octahedron with edge lengths .
The cube has the octahedral group of symmetries, and is an equilateral zonohedron and a rhombohedron. It has 13 axes of symmetry: (axes joining midpoints of opposite edges), (space diagonals), and (axes joining opposite face centroids).

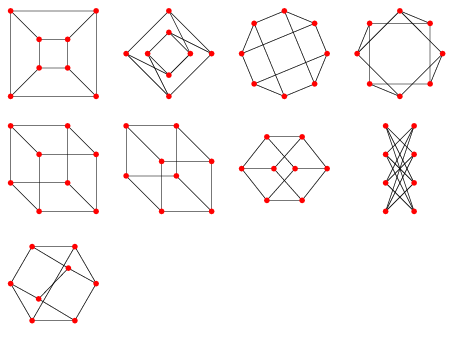
The connectivity of the vertices of the cube is given by the cubical graph.
Using so-called "wallet hinges," a ring of six cubes can be rotated continuously (Wells 1975; Wells 1991, pp. 218-219).

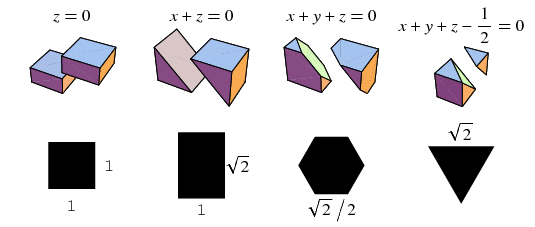
The illustrations above show the cross sections obtained by cutting a unit cube centered at the origin with various planes. The following table summarizes the metrical properties of these slices.

cutting plane	face shape	edge lengths	surface area	volume of pieces
	square	1	1	,
	rectangle	1,		,
	hexagon			,
	equilateral triangle			,

As shown above, a plane passing through the midpoints of opposite edges (perpendicular to a axis) cuts the cube in a regular hexagonal cross section (Gardner 1960; Steinhaus 1999, p. 170; Kasahara 1988, p. 118; Cundy and Rollett 1989, p. 157; Holden 1991, pp. 22-23). Since there are four such axes, there are four possible hexagonal cross sections. If the vertices of the cube are , then the vertices of the inscribed hexagon are , , , , , and . A hexagon is also obtained when the cube is viewed from above a corner along the extension of a space diagonal (Steinhaus 1999, p. 170).

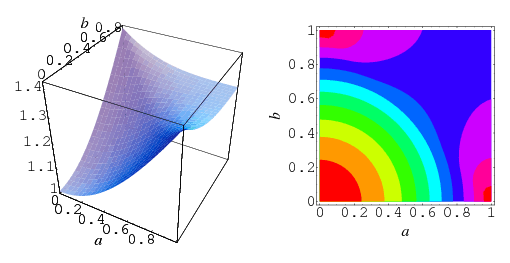
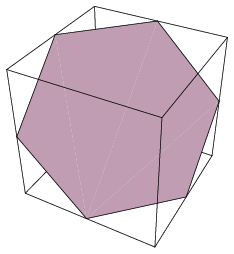
The maximal cross sectional area that can be obtained by cutting a unit cube with a plane passing through its center is , corresponding to a rectangular section intersecting the cube in two diagonally opposite edges and along two opposite face diagonals. The area obtained as a function of normal to the plane is illustrated above (Hidekazu).

A hyperboloid of one sheet is obtained as the envelope of a cube rotated about a space diagonal (Steinhaus 1999, pp. 171-172; Kabai 2002, p. 11). The resulting volume for a cube with edge length is

(10)

(Cardot and Wolinski 2004).

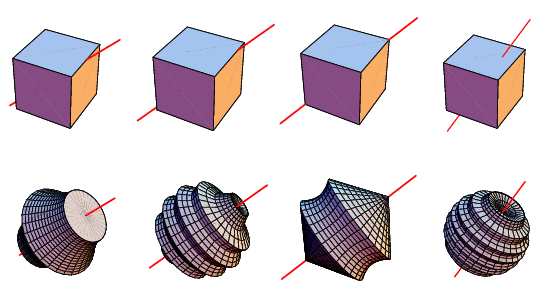
More generally, consider the solid of revolution obtained for revolution axis passing through the center and the point , several examples of which are shown above.

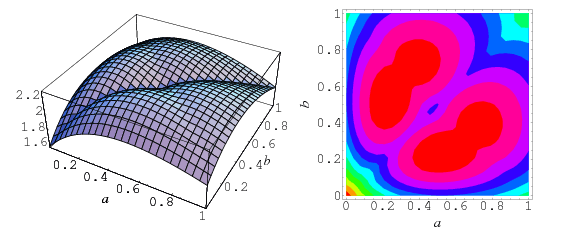
As shown by Hidekazu, the solid with maximum volume is obtained for parameters of approximately . This corresponds to the rightmost plot above.
The centers of the faces of an octahedron form a cube, and the centers of the faces of a cube form an octahedron (Steinhaus 1999, pp. 194-195). The largest square which will fit inside a cube of edge length has each corner a distance 1/4 from a corner of a cube. The resulting square has edge length , and the cube containing that edge is called Prince Rupert's cube.
The solid formed by the faces having the edges of the stella octangula (left figure) as polygon diagonals is a cube (right figure; Ball and Coxeter 1987). Affixing a square pyramid of height 1/2 on each face of a cube having unit edge length results in a rhombic dodecahedron (Brückner 1900, p. 130; Steinhaus 1999, p. 185).
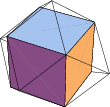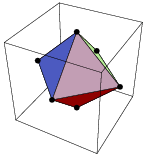
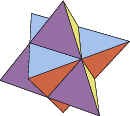
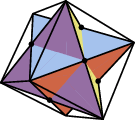
Since its eight faces are mutually perpendicular or parallel, the cube cannot be stellated.
The cube can be constructed by cumulation of a unit edge-length tetrahedron by a pyramid with height . The following table gives polyhedra which can be constructed by cumulation of a cube by pyramids of given heights .

		result
		tetrakis hexahedron
	2	rhombic dodecahedron
		24-faced star deltahedron

The polyhedron vertices of a cube of edge length 2 with face-centered axes are given by . If the cube is oriented with a space diagonal along the z-axis, the coordinates are (0, 0, ), (0, , ), (, , ), (, , ), (0, , ), (, , ), (, , ), and the negatives of these vectors. A faceted version is the great cubicuboctahedron.

Wolfram