 |
 |
 |
 |
 |
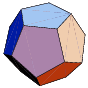
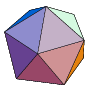
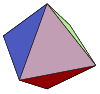
The Platonic solids were known to the ancient Greeks, and were described by Plato in his Timaeus ca. 350 BC. In this work, Plato equated the tetrahedron with the "element" fire, the cube with earth, the icosahedron with water, the octahedron with air, and the dodecahedron with the stuff of which the constellations and heavens were made (Cromwell 1997). Predating Plato, the neolithic people of Scotland developed the five solids a thousand years earlier. The stone models are kept in the Ashmolean Museum in Oxford (Atiyah and Sutcliffe 2003).
Schläfli (1852) proved that there are exactly six regular bodies with Platonic properties (i.e., regular polytopes) in four dimensions, three in five dimensions, and three in all higher dimensions. However, his work (which contained no illustrations) remained practically unknown until it was partially published in English by Cayley (Schläfli 1858, 1860). Other mathematicians such as Stringham subsequently discovered similar results independently in 1880 and Schläfli's work was published posthumously in its entirety in 1901.
If
1. The vertices of
2. All the dihedral angles are equal.
3. All the vertex figures are regular polygons.
4. All the solid angles are equivalent.
5. All the vertices are surrounded by the same number of faces.
Let
| solid | Schläfli symbol | Wythoff symbol | C&R symbol | group | |||
| cube | 3 |
8 | 12 | 6 | |||
| dodecahedron | 3 |
20 | 30 | 12 | |||
| icosahedron | 5 |
12 | 30 | 20 | |||
| octahedron | 4 |
6 | 12 | 8 | |||
| tetrahedron | 3 |
4 | 6 | 4 |
|
(1)
|
|
(2)
| |||
|
(3)
| |||
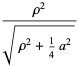 |
(4)
| ||
|
(5)
| |||
|
(6)
| |||
|
(7)
|
| solid | |||
| cube | |||
| dodecahedron | |||
| icosahedron | |||
| octahedron | |||
| tetrahedron |
| solid | |||
| cube | 0.5 | 0.70711 | 0.86603 |
| dodecahedron | 1.11352 | 1.30902 | 1.40126 |
| icosahedron | 0.75576 | 0.80902 | 0.95106 |
| octahedron | 0.40825 | 0.5 | 0.70711 |
| tetrahedron | 0.20412 | 0.35355 | 0.61237 |
| solid | ||
| cube | 1 | 1 |
| dodecahedron | ||
| icosahedron | ||
| octahedron | ||
| tetrahedron |
| solid | ||||
| cube | 90.000 | 70.529 | ||
| dodecahedron | 116.565 | 41.810 | ||
| icosahedron | 138.190 | 63.435 | ||
| octahedron | 109.471 | 90.000 | ||
| tetrahedron | 70.529 | 109.471 |
|
(8)
| |||
|
(9)
| |||
|
(10)
|

The plots above show scaled duals of the Platonic solid embedded in a cumulated form of the original solid, where the scaling is chosen so that the dual vertices lie at the incenters of the original faces (Wenninger 1983, pp. 8-9).
Since the Platonic solids are convex, the convex hull of each Platonic solid is the solid itself. Minimal surfaces for Platonic solid frames are illustrated in Isenberg (1992, pp. 82-83).
Wolfram
댓글 없음:
댓글 쓰기