Ptolemy's Theorem Cyclic Quadrilateral

For a cyclic quadrilateral, the sum of the products of the two pairs of opposite sides equals the product of the diagonals

(Kimberling 1998, p. 223).

Cyclic Quadrilateral

A cyclic quadrilateral is a quadrilateral for which a circle can be circumscribed so that it touches each polygon vertex. A quadrilateral that can be both inscribed and circumscribed on some pair of circles is known as a bicentric quadrilateral.
The area of a cyclic quadrilateral is the maximum possible for any quadrilateral with the given side lengths. The opposite angles of a cyclic quadrilateral sum to 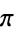radians (Euclid, Book III, Proposition 22; Heath 1956; Dunham 1990, p. 121). There exists a closed billiards path inside a cyclic quadrilateral if its circumcenter lies inside the quadrilateral (Wells 1991, p. 11).
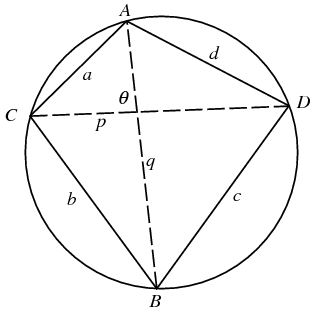
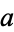
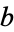
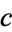
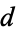
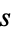
The area is then given by a special case of Bretschneider's formula. Let the sides have lengths , , , and , let be the semiperimeter

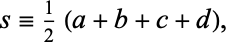(1)

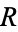
and let be the circumradius. Then

			(2)
			(3)

the first of which is known as Brahmagupta's formula. Solving for the circumradius in (2) and (3) gives

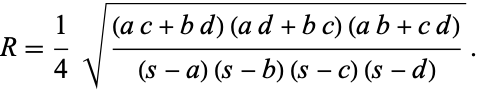(4)

The diagonals of a cyclic quadrilateral have lengths

			(5)
			(6)

so that .
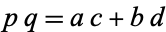
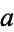
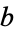
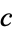
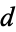
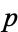
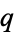
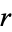
In general, there are three essentially distinct cyclic quadrilaterals (modulo rotation and reflection) whose edges are permutations of the lengths , , , and . Of the six corresponding polygon diagonals lengths, three are distinct. In addition to and , there is therefore a "third" polygon diagonal which can be denoted . It is given by the equation

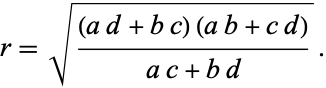(7)

This allows the area formula to be written in the particularly beautiful and simple form

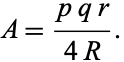(8)

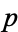
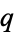
The polygon diagonals are sometimes also denoted , , and .
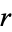
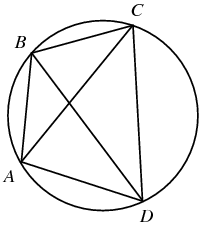
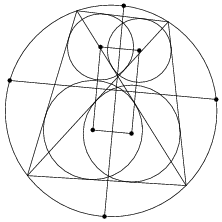
The incenters of the four triangles composing the cyclic quadrilateral form a rectangle. Furthermore, the sides of the rectangle are parallel to the lines connecting the mid-arc points between each pair of vertices (left figure above; Fuhrmann 1890, p. 50; Johnson 1929, pp. 254-255; Wells 1991). If the excenters of the triangles constituting the quadrilateral are added to the incenters, a rectangular grid is obtained (right figure; Johnson 1929, p. 255; Wells 1991).

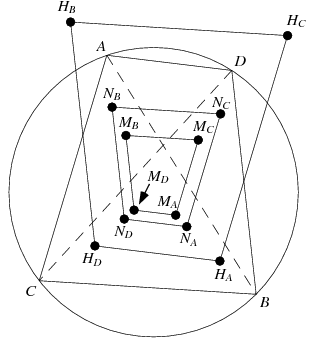
Consider again the four triangles contained in a cyclic quadrilateral. Amazingly, the triangle centroids 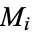, nine-point centers 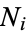, and orthocenters 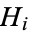formed by these triangles are similar to the original quadrilateral. In fact, the triangle formed by the orthocenters is congruent to it (Wells 1991, p. 44).
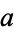
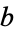
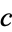
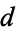
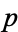
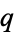
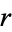
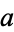
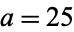
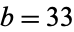
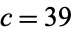
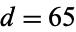
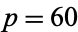
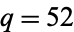
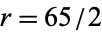
A cyclic quadrilateral with rational sides , , , and , polygon diagonals and , circumradius , and area is given by , , , , , , , and .
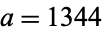
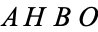
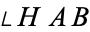
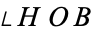
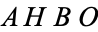
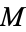
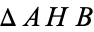
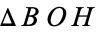
Let be a quadrilateral such that the angles and are right angles, then is a cyclic quadrilateral (Dunham 1990). This is a corollary of the theorem that, in a right triangle, the midpoint of the hypotenuse is equidistant from the three vertices. Since is the midpoint of both right triangles and , it is equidistant from all four vertices, so a circle centered at may be drawn through them. This theorem is one of the building blocks of Heron's derivation of Heron's formula.

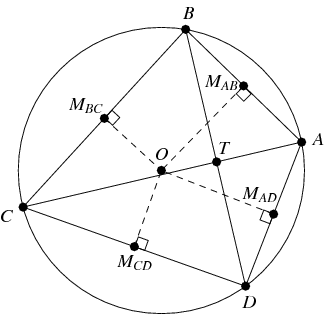
An application of Brahmagupta's theorem gives the pretty result that, for a cyclic quadrilateral with perpendicular diagonals, the distance from the circumcenter 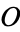to a side is half the length of the opposite side, so in the above figure,

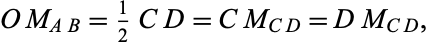(9)

and so on (Honsberger 1995, pp. 37-38).

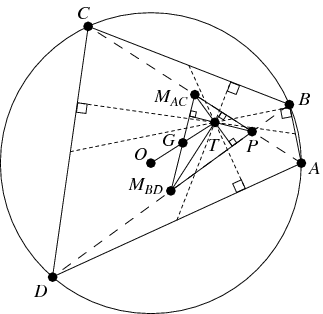
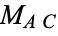
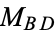
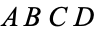
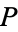
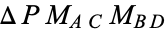
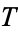
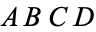
Let and be the midpoints of the diagonals of a cyclic quadrilateral , and let be the intersection of the diagonals. Then the orthocenter of triangle is the anticenter of (Honsberger 1995, p. 39).

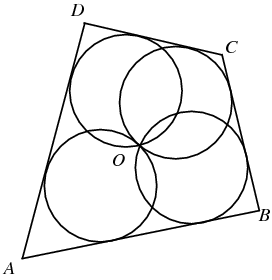
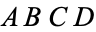
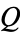
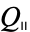
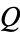
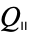
Place four equal circles so that they intersect in a point. The quadrilateral is then a cyclic quadrilateral (Honsberger 1991). For a convex cyclic quadrilateral , consider the set of convex cyclic quadrilaterals whose sides are parallel to . Then the of maximal area is the one whose polygon diagonals are perpendicular (Gürel 1996).
Wolfram