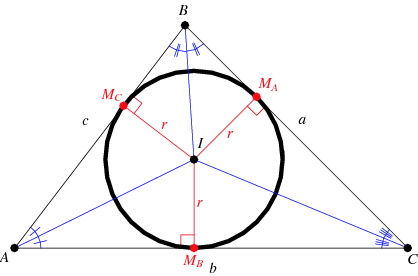
The incenter  is the center of the incircle for a polygon or insphere for a polyhedron (when they exist). The corresponding radius of the incircle or insphere is known as the inradius.
is the center of the incircle for a polygon or insphere for a polyhedron (when they exist). The corresponding radius of the incircle or insphere is known as the inradius.
The incenter can be constructed as the intersection of angle bisectors. It is also the interior point for which distances to the sides of the triangle are equal. It has trilinear coordinates 1:1:1, i.e., triangle center function
(1)
|
(2)
|
The distance between the incenter and circumcenter is 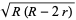 , where
, where 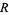 is the circumradius and
is the circumradius and 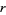 is the inradius, a result known as the Euler triangle formula.
is the inradius, a result known as the Euler triangle formula.
The incenter lies on the Nagel line and Soddy line, and lies on the Euler line only for an isosceles triangle. The incenter is the center of the Adams' circle, Conway circle, and incircle. It lies on the Darboux cubic,M'Cay cubic, Neuberg cubic, orthocubic, and Thomson cubic. It also lies on the Feuerbach hyperbola.
For an equilateral triangle, the circumcenter 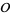 , triangle centroid
, triangle centroid 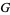 , nine-point center
, nine-point center 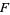 , orthocenter
, orthocenter 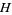 , and de Longchamps point
, and de Longchamps point 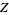 all coincide with
all coincide with 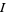 .
.
The distances between the incenter and various named centers are given by
(3)
| |||
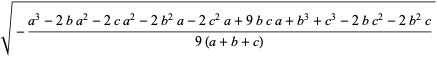 |
(4)
| ||
(5)
| |||
(6)
| |||
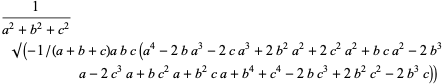 |
(7)
| ||
(8)
| |||
(9)
| |||
(10)
| |||
(11)
| |||
(12)
| |||
(13)
| |||
(14)
|
where 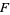 is the Feuerbach point,
is the Feuerbach point, 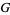 is the triangle centroid,
is the triangle centroid, 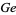 is the Gergonne point,
is the Gergonne point, 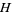 is the orthocenter,
is the orthocenter, 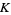 is the symmedian point,
is the symmedian point, 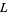 is the de Longchamps point,
is the de Longchamps point, 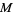 is the mittenpunkt,
is the mittenpunkt, 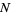 is the nine-point center,
is the nine-point center, 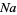 is the Nagel point,
is the Nagel point, 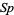 is the Spieker center,
is the Spieker center, 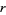 is the inradius,
is the inradius, 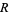 is the circumradius,
is the circumradius, 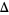 is the triangle area, and
is the triangle area, and 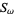 is Conway triangle notation.
is Conway triangle notation.
The following table summarizes the incenters for named triangles that are Kimberling centers.
The circle power of the incenter with respect to the circumcircle is
(15)
|
(Johnson 1929, p. 190).
댓글 없음:
댓글 쓰기