숫자 1에 담긴 수학

우리는 태어나자마자 한 살이 되고, 학교는 1학년부터 시작된다. 이처럼 숫자 1은 시작을 의미한다. 시작, 처음과 같은 설렘을 안고 숫자 1에 담긴 수학 이야기를 만나 보자.

네 가지 그림에서 떠오르는 숫자는 무엇일까? <출처: gettyimages(왼쪽 위, 오른쪽 위), sxc.hu(왼쪽 아래, 오른쪽 아래)>

자연수 집합을 만드는 1

숫자 1은 일종의 티끌이다. 무슨 말일까? 1에 1을 차례로 더하면 2, 3, 4, 5,… 등 모든 자연수를 만들 수 있다. 즉, 1을 이용해 자연수라는 큰 집합을 만드는 것이다. 이런 숫자 1의 역할은 19세기 이탈리아의 수학자인 주세페 페아노(Giuseppe Peano, 1858~1932)가 자연수 집합을 정의하기 위해 제시한 페아노 공리계에서 잘 드러난다. 수학에서 공리란, 어떤 이론의 기초로서 증명 없이 받아들이는 명제를 말한다.

이게 도대체 무슨 말인가 의아할 수 있다. 하지만 조금만 생각해 보면 페아노 공리계가 당연한 사실을 이야기하고 있다는 걸 깨닫게 된다. 우선 1이 자연수라는 첫 번째 공리는 매우 당연하다. 또한 1의 다음 수는 2, 2의 다음 수는 3인 것처럼 어떤 자연수 n 다음에는 자연수 n+1이 존재한다. 세 번째 공리에서는 어떤 자연수 n의 다음 수인 n+1=1이 되려면 n=0이 돼야 하기 때문에, 어떤 자연수의 다음 자연수는 1이 될 수 없다는 걸 이해할 수 있다.

네 번째 공리 역시 서로 다른 두 자연수 3과 4, 그리고 그다음 자연수인 4와 5가 다른 것을 바로 확인할 수 있다. 다섯 번째 공리는 지금까지 살펴본 이전의 4개 공리를 만족하는 여러 집합 중 가장 작은 집합은 자연수 집합이라는 의미를 갖고 있다. 페아노 공리계에서 보듯 1은 자연수의 시작점이자, 자연수 집합을 만들어 내는 중요한 티끌이다.

소수도, 합성수도 아닌 1

1은 소수일까? 합성수일까? 두 질문에 대한 답은 둘 다 ‘No’이다. 특이하게도 1은 자연수 중에서 유일하게 소수도 아니고, 합성수도 아닌 수다. 소수란 양의 약수가 1과 자신뿐인, 1보다 큰 자연수를 말한다. 따라서 소수는 약수를 2개만 갖는다. 북한에서는 소수를 ‘씨수’라고 부르는데, 그 이유가 수학적이다. 어떤 자연수라도 소인수분해를 통해 소수들의 곱으로 나타낼 수 있다. 따라서 모든 자연수의 근원은 소수라고 생각할 수 있다. 그런 점에서 북한에서 소수를 씨앗이 되는 수, 씨수라고 부르는 것이다.

그러면 1은 왜 소수가 될 수 없을까? 만약 1을 소수로 받아들인다면, 숫자 10을 소인수분해한 결과가 2X5 단 한 가지만 나오는 것이 아니라 1x2x5, 12x2x5, 13x2x5, ... 등 다양한 형태로 나타난다. 이것은 어떤 수를 소인수분해 했을 때, 단 한 가지 형태로 나타나야 한다는 산술의 기본정리에 어긋나는 것이다. 따라서 1은 소수가 되기에는 적당하지 않다. 그렇다면 자연수 중에 소수는 몇 개나 있을까? 자연수가 무한히 많은 수들로 이루어져 있듯, 소수의 개수도 무한하다.1)이 사실에 대한 증명은 기원전 3세기경 그리스의 수학자 유클리드(Euclid, BC330?~BC275?)가 쓴 책인 [유클리드 원론]에 기록돼 있을 정도로 역사가 매우 깊다.

제곱을 해도 값이 같은 1

모두 1로 이루어진 자연수를 제곱하면, 1부터 n의 자리까지 자연수가 순서대로 점점 커졌다가 다시 점점 작아지는 신기한 답이 나온다.

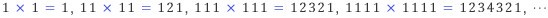
그 이유는 4자리의 자연수 1111을 제곱한 계산 과정에서 찾아볼 수 있다.

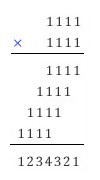
위의 계산을 살펴보면, 11112=1111×1111=1111+11110+111100+1111000이 된다. 따라서 일의 자리에서 1, 십의 자리에서 1+1, 백의 자리에서 1+1+1, ... 이런 식으로 1이 차곡차곡 더해진 결과 1234321이란 답이 나오는 것이다. 이 계산 과정에서 1의 성질을 찾을 수 있다. 1은 0을 제외하고 원래의 값(=1)과 제곱한 값(=12)이 같은 유일한 수다. 이를 방정식으로 나타내면 다음과 같다.

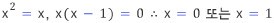
0도 원래의 값과 제곱한 값이 같기 때문에 0×0=0, 00×00=000, 000×000=00000과 같이 쓸 수는 있다. 하지만 각 자리의 값이 0인 수는 모두 0이므로 의미가 없다.

위에서 본 계산 과정에 따라 9자리의 자연수 111111111을 제곱한 값은 12345678987654321이라는 것을 쉽게 알 수 있다. 하지만 이 계산은 각 자리의 값이 모두 1로 이루어진 9자리의 자연수까지만 적용이 된다. 9자리를 넘게 되면 덧셈의 과정에서 올림이 일어나므로 위의 규칙을 완벽하게 적용할 수 없기 때문이다. 예를 들어, 1로 이루어진 10자리 자연수 1111111111을 제곱하면 덧셈의 과정에서 앞의 자리로 올림이 일어나 답은 1234567900987654321이 된다.

벤포드의 법칙과 1

벤포드는 상용로그표의 앞부분, 즉 1부터 10중 1에 가까운 숫자를 더 많이 찾아보았다는 사실을 발견하고, 벤포드의 법칙을 만들었다.

기업의 가계부에 해당하는 대차대조표를 보면 재미있는 현상을 확인할 수 있다. 1로 시작하는 경우가 전체의 약 30%를 차지한다는 사실이다. 각 숫자가 나올 확률은 숫자 1부터 9까지 동일하게 100÷9≒11.1%가 나와야 한다. 그런데 왜 1이 30%라는 큰 비율로 나오는 걸까?

1937년 미국 가전회사인 GE의 물리학자 프랭크 벤포드(Frank Benford, 1883~1948)는 자신이 사용하던 상용로그표 페이지를 넘기다가 이 신기한 사실을 발견하고는 벤포드의 법칙 2)을 만들었다. 상용로그표에서 벤포드가 신기하다고 생각한 점은 로그표의 앞부분이 뒷부분보다 더 때가 타고 너덜너덜해졌다는 점이었다. 이것은 상용로그표의 앞부분, 즉 1부터 10 중 1에 가까운 숫자를 더 많이 찾아보았다는 것을 의미한다. 벤포드는 왜 찾아본 수가 고르게 분포하지 않고 1에 가까운 쪽에 집중됐는지 궁금했다. 그래서 다른 통계에도 이런 경향이 있는지 확인해 보았다. 그러자 놀랍게도 인구, 주식, 소득, 매출, 야구 기록, 강의 길이 등 다른 여러 경우에서 이와 같은 현상을 발견할 수 있었다. 벤포드는 통계의 어떤 항목의 값이 1부터 9까지 각각의 숫자로 시작할 확률을 정리해 다음과 같은 결과를 얻었다.

인구수의 예를 통해 벤포드의 법칙에 대해 간단히 접근해 보자. 한 도시의 인구가 10년 만에 1만 명에서 2만 명으로 증가했을 때, 다음 10년 뒤 인구는 어떻게 될까? 얼핏 3만 명이라고 생각할 수도 있지만, 실제 인구의 증가는 곱셈과 연관돼 이루어진다. 따라서 처음 1만 명에서 10년 만에 2배가 되어 2만 명이 되고, 다시 10년 뒤 인구는 2만 명의 2배인 4만 명으로 늘어난다. 이렇게 10년 단위로 2배씩 변화하는 인구수를 표로 나타낸 뒤, 각 수가 어떤 숫자로 시작하는지 확인해 보자.

위의 표에서 20개의 숫자 중 1로 시작하는 건 6번, 2로 시작하는 건 4번, 3으로 시작하는 건 2번인 것을 확인할 수 있다. 그 확률은 각각 (6/20)×100=30(%), (4/20)×100=20(%), (2/20)×100=10(%)로 벤포드가 구한 결과와 비슷하다. 모든 통계의 결과가 벤포드의 법칙을 따르는 것은 아니지만, 통계의 항목들 중에 곱셈과 관련이 있는 건 벤포드의 법칙을 적용할 수 있다. 따라서 곱셈과 관련 있는 통계 항목에서 각 값의 처음 숫자가 1, 2, 3이 아닌 다른 숫자가 더 많이 나타나거나 모든 숫자들이 같은 빈도로 나타난다면, 이 장부는 누군가 허위로 조작했을 가능성이 크다. 실제로 미국의 몇 몇 주에서는 횡령, 조작, 탈세 등을 탐지하기 위해 벤포드의 법칙을 활용하고 있다.

1은 자연수 중에서도 가장 작고, 약수도 1개뿐인 볼품없는 수로 생각하기 쉽다. 그러나, 숫자 1이 쌓은 튼튼한 기초는 수학이 더 많은 발전을 이룰 수 있는 든든한 버팀목이 되고 있다.

소수의 개수는 무한하다

소수를 최대한 많이 찾아보았을 때, n개의 서로 다른 소수를 발견했다고 하자.

P₁, P₂, P₃, P₄, …, P_n

더 이상 소수를 찾을 수 없다면 소수는 n개뿐이므로 유한개일 것이다. 하지만 아래의 소수를 1개씩 계속 추가할 수 있다. 먼저 발견한 n개의 소수를 모두 곱한 뒤에 1을 더한 수를 P라고 하자.

P = P₁ × P₂ × P₃ × P₄ × … × P_n+1

이 때, P는 P₁, P₂, P₃, P₄, …, P_n 중 어떤 소수로도 나누어지지 않는다. 또한 P는 1보다 크므로 소수나 합성수이다.

case 1) P가 소수일 때
P는 n개의 소수 중 어떤 수로도 나누어지지 않으므로, 약수가 1과 자기 자신밖에 없는 소수가 된다. 결국 처음에 미처 찾지 못한 소수 P를 1개를 더 발견한 것이므로, n+1번째 소수 Pn+1=P가 추가된다.

case 2) P가 합성수일 때
P가 합성수라면 P는 1과 자기 자신 외에 소수인 약수 p를 갖게 된다. 그런데 이 p는 P1, P2, P3, P4, …, Pn 중 어떤 소수와도 같지 않으므로 역시 처음에 찾지 못한 소수를 1개 더 발견한 것이 된다. 따라서 n+1번째 소수 Pn+1=p를 추가하게 된다.

결국 처음에 최대한 찾은 소수가 n개이더라도, 위와 같은 방법으로 이전에 미처 발견하지 못한 소수를 1개씩 더 찾아낼 수 있고, 이 방법은 무한히 반복 가능하므로 소수의 개수는 무한하다.

2벤포드의 법칙의 이유

벤포드의 법칙은 통계의 많은 항목의 값이 곱셈과 관련이 깊기 때문에 발생한다. 값이 곱셈과 관련해 나타난다면, 그 값 y 는 상수 k 와 t 에 대해 y = k t ^x 과 같이 나타낼 수 있다. 이 때, y 가 m +1 자리이면서 처음 숫자가 자연수 a 가 된다는 것은 다음 부등식을 만족하는 것이다.

a ×10^m ≤ kt^x < (a+1) × 10^m

양 변에 상용로그를 씌우면, m + loga ≤ logk + xlogt < m + log(a+1)

따라서 이 조건을 만족하는 x값의 범위는 두 수 loga와 log(a+1) 사이의 차와 비례한다. 그런데 자연수 a에 대하여 loga와 log(a+1)의 차는 다음과 같이 a=1일 때 0.3010으로 가장 크다는 것을 볼 수 있다. 또한 다음 표의 값을 100배하여 1의 자리까지 반올림한 값을 b라 하고 나타내면, 그 값이 벤포드가 조사한 확률과 거의 같다는 것을 확인할 수 있다.

　　

• 네이버캐스트