수학의
역사는 수학자들이 어려운 문제들을 풀기 위해 벌여온 사투의 기록이라 할 수 있다. 이 과정에서 새로운 개념, 놀라운 아이디어가 등장하고, 여기서
다시 파생된 문제에 도전하는 과정이 끊임 없이 반복된다. 수학에서 어려운 문제란 문제가 무엇인지 이해하기도 힘든 경우가 대부분이지만, 초등학생도
이해할 수 있는 문제이면서도 전혀 해결의 실마리가 보이지 않는 문제도 드물지 않다.
1937년,
박사 학위를 받은 지 겨우 2년 남짓 된 독일의 젊은 수학자 로타르 콜라츠(Lothar Collatz,
1910~1990)는 아주 단순하면서도 재미있는 문제를 제시하였다. 그의 이름을 따서 콜라츠의 추측이라 불리는 이 문제는 다음과 같다.
자연수를
하나 고른다. 이 수가 짝수면 2로 나누고, 홀수면 3을 곱한 다음 1을 더한다. 다시 그 수가 짝수면 2로 나누고, 홀수면 3을 곱한 다음
1을 더한다. 이 과정을 반복하면 그 수가 항상 1이 될까?
이
추측은 3을 곱하고 1을 더하는 과정 때문에 “3n+1 문제”로 불리기도 한다. 처음에 고른 수가 3이면, 3은 홀수이므로 다음 수는 3x3+1
= 10이고, 10은 짝수이므로 다음 수는 5이다. 이 과정을 반복하면 다음과 같다.
수가
잠깐 커지기는 하지만, 짝수가 될 때마다 절반씩 줄어들므로, 이 추측은 어느 정도는 당연해 보이기도 한다. 이번에는 7로 시작해 보자. 이 경우
그 결과는 다음과 같다.
줄어들
듯 줄어들 듯 하면서 중간중간 커지더니 16단계에서야 겨우 1이 된다. 이처럼 수가 커졌다 작아졌다를 반복하다가 어느 순간 계속 작아져 1이
되는 모습이 마치 우박이 구름 속에서 오르내리며 자라다가 지상으로 떨어지는 것과 비슷하다는 뜻에서 이 수들을 “우박수(hailstone number)”로
부르기도 한다.
언뜻
보기에는 어떤 수에서 시작하든 우박수는 조금 커지다가 곧 작아질 것처럼 보인다. 앞의 예에서 7이 조금 많은 단계를 거치긴 하지만, 나타나는
수들이 그리 크지는 않다. 그러나 예상과 달리 그리 크지 않은 수에서 시작하여 깜짝 놀랄 만큼 급격하게 우박수가 커지는 경우가 있다. 바로
27이 그런 수이다.
이렇게
차츰 커지던 수는 77번째 단계에서 무려 9232가 되어, 이러다 한없이 커지는 게 아닐까 걱정될 즈음, 급격하게 작아지기 시작하여 30단계를
더 나아간 111번째 단계에서 1이 된다. 다음 그림은 27에서 시작하여 각 단계마다 등장하는 우박수들을 나타내어 선으로 연결한 것이다.
77번째 단계에서 9000을 넘는 것을 볼 수 있다.
콜라츠가
이 문제를 제기한 이후, 수많은 사람들이 반례를 찾기 위해 노력하였다. 단 하나의 반례만 있어도 콜라츠의 추측은 거짓이 된다. 그러나 몇 십 년
동안의 노력에도 불구하고 단 하나의 반례도 발견되지 않았다. 컴퓨터 시대가 도래한 이후, 엄청나게 큰 범위의 수까지 콜라츠 추측이 성립하는지
조사할 수 있게 되었다. 현재의 기록은 19 × 258 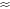 5.48 × 1018보다 작은 모든 수에
대해 콜라츠 추측이 성립함이 확인되어 있다. 이쯤 되면 이 추측이 거짓일 리는 없어 보이지만, 상상을 초월하는 범위에서 반례가 존재할 가능성이
전혀 없는 것은 아니다. 반례를 찾는 것이라면 이런 과정을 통해서도 가능하겠지만, 무한히 많은 모든 자연수에 대해 추측이 참임을 증명하려면
추측이 내포하고 있는 수학적인 구조를 모르고서는 가망이 없는 일이다. 이런 구조를 밝혀내는 것이야말로 수학이 추구하는 것이며, 이런 과정을 통해
수학은 더욱 발전하게 된다.
5.48 × 1018보다 작은 모든 수에
대해 콜라츠 추측이 성립함이 확인되어 있다. 이쯤 되면 이 추측이 거짓일 리는 없어 보이지만, 상상을 초월하는 범위에서 반례가 존재할 가능성이
전혀 없는 것은 아니다. 반례를 찾는 것이라면 이런 과정을 통해서도 가능하겠지만, 무한히 많은 모든 자연수에 대해 추측이 참임을 증명하려면
추측이 내포하고 있는 수학적인 구조를 모르고서는 가망이 없는 일이다. 이런 구조를 밝혀내는 것이야말로 수학이 추구하는 것이며, 이런 과정을 통해
수학은 더욱 발전하게 된다.
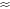 5.48 × 1018보다 작은 모든 수에
대해 콜라츠 추측이 성립함이 확인되어 있다. 이쯤 되면 이 추측이 거짓일 리는 없어 보이지만, 상상을 초월하는 범위에서 반례가 존재할 가능성이
전혀 없는 것은 아니다. 반례를 찾는 것이라면 이런 과정을 통해서도 가능하겠지만, 무한히 많은 모든 자연수에 대해 추측이 참임을 증명하려면
추측이 내포하고 있는 수학적인 구조를 모르고서는 가망이 없는 일이다. 이런 구조를 밝혀내는 것이야말로 수학이 추구하는 것이며, 이런 과정을 통해
수학은 더욱 발전하게 된다.
5.48 × 1018보다 작은 모든 수에
대해 콜라츠 추측이 성립함이 확인되어 있다. 이쯤 되면 이 추측이 거짓일 리는 없어 보이지만, 상상을 초월하는 범위에서 반례가 존재할 가능성이
전혀 없는 것은 아니다. 반례를 찾는 것이라면 이런 과정을 통해서도 가능하겠지만, 무한히 많은 모든 자연수에 대해 추측이 참임을 증명하려면
추측이 내포하고 있는 수학적인 구조를 모르고서는 가망이 없는 일이다. 이런 구조를 밝혀내는 것이야말로 수학이 추구하는 것이며, 이런 과정을 통해
수학은 더욱 발전하게 된다.
콜라츠
추측이 대체로(?) 참이 된다는 것을 확률적인 접근 방법으로 그럴 듯하게 설명할 수 있다. 이런 식의 설명 방법을 발견술적(heuristic)이라고
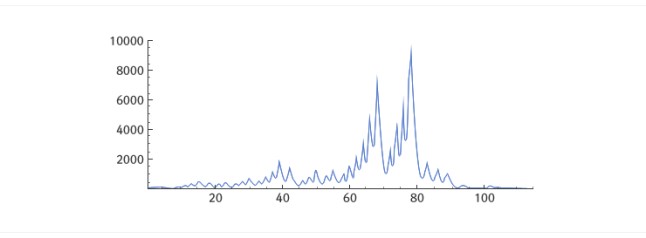
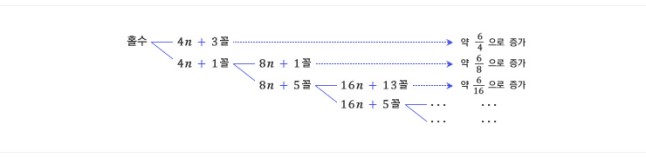
한다. 우선 모든 짝수는 바로 다음 단계에 절반으로 크기가 줄어든다. 이제 홀수에 대해 생각해 보자. 4로 나누어 3이 남는 홀수는 4n+3으로
쓸 수 있다. 이 수는 첫 단계에 12n+10으로 커지지만, 두 번째 단계를 거치면 새로운 홀수 6n+5가 되어 처음에 비해 약 6/4 정도로
커진다. 4로 나누어 1이 남는 홀수를 다시 8로 나눈 나머지에 따라 분류하면 8n+1과 8n+5 꼴의 두 가지가 되고, 이 가운데 8n+1
꼴의 홀수는 새로운 홀수 6n+1이 되어 6/8 정도로 작아진다.
8n+5
꼴의 홀수는 16n+5와 16n+13 꼴의 두 가지가 가능하고, 16n+13은 6/16 정도로 작아진 6n+5가 된다.
이와
같이 생각하면, 홀수의 절반은 6/4으로 늘어나고, 나머지의 절반은 6/8으로 줄어들고, 다시 나머지의 절반은 6/16으로 줄어들어, 이 과정을
반복하면 홀수 전체는 평균적으로 3/4 정도로 작아진다고 생각할 수 있다.
따라서
확률적으로 생각하면 어떤 수로 시작하든 결국은 계속 줄어들어 1이 될 수밖에 없다.
당연한
일이겠지만, 콜라츠 추측의 3n+1을 바꾸었을 때 어떤 일이 생기는지도 많은 사람들이 연구하였다. 만약 3n+1 대신 3n-1로 계산한다면
어떻게 될까? 즉, 짝수는 2로 나누고, 홀수는 세 배한 다음 1을 뺀다. 이 경우에도 어떤 수에서 시작하든 항상 1이 될까? 홀수에 대해
생각해 보면, 그 다음 수는 3n+1보다 더 작은 3n-1을 생각하게 되니, 당연히 더 쉽게 1이 될 것 같다. 실제로 발견술적인 설명을 여기에
적용하면, 콜라츠 추측과 비슷한 방법으로 계산하여, 홀수는 평균적으로 3/4 정도로 작아진다고 할 수 있다. 그러니 수가 계속 작아져서 결국
1이 되는 것이 너무나도 당연해 보인다. 그러나 3n-1로 계산하는 경우, 놀랍게도 반례가 존재한다. 처음에 5로 시작하게 되면, 다음과 같이
다섯 단계 만에 다시 처음 숫자인 5가 나와 버린다. 1이 되지 않고 계속 순환하는 경우가 존재한다.
이와
같이 1이 되지 않는 순환은 하나 더 있어서, 다음의 경우처럼 17에서 시작하면, 18번째 단계에 다시 17이 된다.
이
결과는 108까지의
수를 대상으로 확인한 것으로, 또 다른 반례가 되는 순환이 존재하는지는 알려져 있지 않다.
발견술적인
설명은 꽤 그럴 듯하다. 실제로 이와 비슷한 방법으로 콜라츠 추측이나 골드바흐 추측 같은 수학의 미해결 문제를 풀었다고 주장하는 사람도 있다.
그러나 이 설명은 어디까지나 확률적으로 생각하는 것이므로, 이것으로 증명이 되었다고 할 수는 없다. 무엇보다도 이 방법은 홀수에서 출발하여
새로운 홀수를 만들 때마다, 그 홀수가 골고루 나타난다는 가정에 바탕하고 있다. 콜라츠 추측에서 만들어지는 수들이 확률적으로 고르게 나타난다는
것을 증명하는 것은 콜라츠 추측 자체를 증명하는 것만큼이나 어려운 일이다. 또, 변형식인 3n-1처럼 확률적으로는 극히 작은 반례가 존재할
가능성도 여전히 있다. 어쩌면 콜라츠 추측 또한 반례 하나로 거짓이 되어버릴 수도 있다. 이처럼 발견술적인 설명은 글자 그대로 그럴 듯한 어떤
사실을 생각해내는 데는 도움이 되지만, 엄밀한 증명과는 거리가 멀다고 할 수 있다. 그러나 이 두 가지가 별개의 것은 아니어서, 위대한
수학자들은 발견술적인 착상과 엄밀한 증명의 두 가지에 모두 능통한 경우가 많다.
어려워
보이는 문제가 간단한 아이디어로 해결되는가 하면, 반대로 간단해 보이는 문제가 온갖 최신 이론을 총동원하여도 난공불락인 경우가 있다. 콜라츠
추측이 놀라운 아이디어로 허무하게 해결될 가능성도 없지는 않지만, 지금까지의 역사를 보면 여기에는 아직 우리가 알아차리지 못한 특별한 수학적
구조가 숨어 있는 것 같다. 이런 구조를 밝혀내고 일반화할 수 있다면 수학은 또 한 단계 도약하게 될 것이다. 끝으로, 1500편이 넘는 논문을
발표하였던 헝가리의 위대한 수학자 폴 에르되시(Paul Erdős,
1913~1996)가 콜라츠 추측에 대해 남긴 인상적인 평을 소개하는 것으로 글을 마무리하겠다.






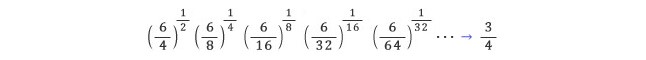
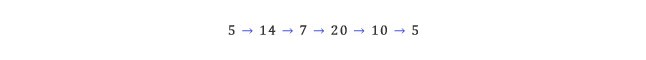

댓글 없음:
댓글 쓰기