(스포일러
주의.) 이 글에는 지난 수학 산책(피보나치 돌 줍기 게임)에 소개한 돌 줍기 게임의 필승 전략이 들어 있다. 돌 줍기 게임을 다시 한번 소개하자면
아래와 같다.
예를
들어 피보나치 수가 아닌 12개의 돌로 시작했다고 하자. 처음에 몇 개의 돌을 집어야 갑이 이길 수 있을까? 필자의 전략은 의외로 단순하다.
12보다 작은 피보나치 수로는 8이 있다. 따라서 8을 을에게 남기면 (물론 3개 이하로 돌을 집어 와서) 이긴다는 걸 안다. 그럼 아예 이
둘의 차에 해당하는 4개로 시작했다고 생각하고, 먼저 이 네 개짜리에서 승리하면 어떨까? 감이 오는가?
그럼
20개로 시작했다면? 이 경우 피보나치 수 13개를 상대방에게 넘겨야 한다. 따라서 일곱 개로 시작했다고 보면 된다. 7개로 시작한 경우 이미
승리 전략을 분석한 바 있다. 기억이 안 나거나 이마저도 따지기 싫으면, 이번에도 7보다 작은 피보나치 수 5개를 넘긴다는 데 착안한다. 따라서
맨 처음에 2개를 줍는 것이 승리 전략임을 알 수 있다! 잠깐. 그럼 18개로 시작했다면? 피보나치 수 13을 뺀 다섯 개로 시작했다고 보면
되는데 이건 어떻게 하나? 쉽다. 다섯 개 다 집는다! 고민 해결.
그런데
위와 같은 방법을 쓰면 항상 이긴다는 걸 어떻게 보장할까? 설령 필자가 이런 전략으로 오천만 명과 대결해 승리했다고 해도, 그것만으로는 증명이라
할 수 없다. 증명이 필요한데… 이런 사소한 놀이의 승리 전략 따위를 시시콜콜 증명할 필요까지 있느냐 싶긴 하다. 하지만, 조금만 참고 훑어
보는 아량을 베풀어 주면 고맙겠다.
지난
번에 피보나치 돌줍기 게임에 대한 글을 쓴 후, 필승 전략을 최초로 알아낸 사람이 누군지 궁금해졌다. 요새 발달한 인터넷 검색을 이용했더니
피보나치 수열을 중심으로 하는 수학을 다루는 ‘피보나치 계간지(TheFibonacci Quarterly)’
창간해인 1963년 12월호에서 쉽게 찾을 수 있었다. 그 논문에서 특히 눈길이 간 것은 논문의 저자 마이클 위니한이 당시 고등학생이었다는
사실이다. 다섯 쪽짜리 논문인데 실제 핵심 부분은 두 쪽 남짓하다. 고등학생다운(?) 풋풋한 논문이라 그대로 소개하기보다는, 조금 변형하여
소개하는 것이 마땅하겠다. 그에 앞서 벨기에의 의사 겸 수학자였던 제켄도르프(Edouard Zeckendorf,
1901-1983)의 이름을 딴 정리에 대해 얘기해 보자.
20개로
시작했을 때의 승리 전략을 되돌아 보자. 먼저 20에서 가장 큰 피보나치 수 13을 빼고 7을 남겼고, 남은 7에서도 피보나치 수 5를 빼어
2를 남겼다. 이 수는 피보나치 수다. 따라서 20은 다음처럼 피보나치 수의 합으로 쓸 수 있다.
사실 모든 자연수는 가장 큰 피보나치 수를 빼 나가는 알고리즘을 쓰면, (전산 용어로 ‘욕심쟁이 알고리즘’(greedy algorithm)이라 부르는 예다) 항상 피보나치 수의 합으로 쓸 수 있다. 예를 들어 100은 다음처럼 쓸 수 있다.
이와 같이 자연수를 피보나치 수의 합으로 표현하는 것을 ‘제켄도르프 분해’라 부른다.
잠깐.
1과 2는 피보나치 수니까, 당연히 모든 수는 피보나치 수의 합으로 쓸 수 있는 것 아닌가? 하지만 이 분해는 독특한 특성을 한 가지 더 갖고
있다. 중복되거나 연속되는 피보나치 수가 나오지 않기 때문이다. 어떤 수를 분해했을 때 인접한 피보나치 수의 합, 예를 들어 13+8이나
5+3이 등장했다면, 애초에 21이나 8이라는 피보나치 수로 먼저 분해할 수 있기 때문이다. 8+8처럼 같은 항이 반복되는 경우,
8+5+3=13+3 등으로 이해하면 인접하지 않는 피보나치 수의 합으로 다시 쓸 수 있음도 알 수 있다. 더 나아가서, 이처럼 자연수를
인접하지도 중복하지도 않게 피보나치 수의 합으로 나타내는 방법은 딱 하나뿐임을 증명할 수 있다. 증명이 그다지 어렵지 않으므로, 여러분도 생각해
보길 바란다.
아래에작은
수의 제켄도르프 분해를 나열했는데, f2 = f1 =
1은 모두f2 로만 표기했음에 유의하자.
이제부터
N의 제켄도르프 분해에서 나타나는 가장 작은 피보나치 수를 Z(N)이라 쓰기로 하자. 앞서 든 예를 보자면 Z(20)=2, Z(100)=3이다.
N이 피보나치 수라는 것과 Z(N)=N이라는 것은 같은 얘기라는 것도 알 수 있다. 그러면, 필자가 사용한 승리 전략은 다음처럼 표현할 수
있다.
Z(N)개의 돌을 집는 것이 승리 전략이다.
이
전략이 정말로 필승 전략이라는 것을 어떻게 증명하는지 얼개만 보자. 돌멩이의 수가 N개이고, 집을 수 있는 돌의 개수가 M개 이하일 때 순서쌍
(N,M)으로 나타내기로 하자. 예를 들어 돌 12개로 시작했다면 순서쌍 (12,11)로 쓸 수 있고, 갑이 그 중 두 개를 집었다면 을은
(10,4)를 건네 받게 된다. 다시 을이 3개를 집었다면 갑은 (7,6)을 건네 받는 셈이다. 따라서 어떤 순서쌍을 넘겨 받아야, 최선을 다할
경우 항상 이기냐는 문제로 표현할 수 있다.
이제
주어진 순서쌍 (N,M)이 ‘필승조’라는 것은 M이 Z(N) 이상일 때를 말하고, ‘패전 처리조’는 반대의 경우를 가리키기로 하자. 이때 다음
두 가지 사실을 증명하면 바라던 증명이 완성된다. (왜일까?)
1.(N,M)이
필승조인 경우, Z(N)개의 돌을 집으면 (N-Z(N),2Z(N))은 항상 패전 처리조다.
2.(N,M)이 패전 처리조인 경우, K개의 돌을 집은 (N-K,2K)는 항상 필승조다. 물론 K는 1이상 M이하의 수여야 한다.
2.(N,M)이 패전 처리조인 경우, K개의 돌을 집은 (N-K,2K)는 항상 필승조다. 물론 K는 1이상 M이하의 수여야 한다.
예를 들어 30개의 돌로 시작했다고 하자. 즉 (30,29)로 시작한 상황이다. 30=21+8+1이므로 Z(30)=1이다. M=29가 Z(30)=1 이상이므로 필승조다. 이때 1개를 집으면 상대방은 (29,2)를 넘겨 받는데, 이는 항상 패전 처리조라는 뜻이다. 실제로 Z(29)=8이 2보다 크다는 것을 확인할 수 있다.
한편
순서쌍 (29,2)를 넘겨 받은 사람은 아무리 발버둥을 쳐도 상대방에게 필승조를 넘겨 준다. 즉, 1개를 집은 (28,2)나, 2개를 집은
(27,4) 모두 필승조다. 28=21+5+2이므로 Z(28)=2이고, 27=21+5+1에서 Z(27)=1이므로 사실임을 확인할 수
있다.
첫
번째 사실의 증명은 대단히 쉬운데, 피보나치 수의 다음다음 항이 원래 수의 2배보다 크기 때문이다. 제켄도르프의 정리를 잘 이용하면, 두 번째
사실의 증명은 다음 도움정리의 증명으로 귀결된다.
예를 들어 F에 대한 수학적 귀납법 등을 이용하면 어렵지 않게 증명할 수 있다.
제켄도르프
분해를 이용하면 자연수마다 0과 1로 이루어진 2진 부호를 할당할 수 있다. 천마디 말보다 하나의 예가 낫겠다. 예를 들어
에
2-1번째, 6-1번째, 9-1번째, 11-1번째, 13-1번째 자리에 1을 부여하고 나머지 자리에는 0을 부여한 뒤, 맨 끝에 1을 하나
덧붙인 부호 1000100101011을 대응한다. 자연수에 이와 같은 방법으로 대응한 부호를 ‘피보나치 부호’(Fibonacci code)
혹은 ‘카우츠(Kautz)-제켄도르프
부호’라 부른다. 맨 마지막은 항상 11이고 그 외에는 1이 중복해서 나오지 않으므로 11이 이 부호의 끝을 알리는 구분자(separator)
역할을 한다는 것을 알 수 있다.
피보나치
부호는 자연수에 따라 길이가 변하고 길이가 쓸데 없이 길어지는 부호처럼 보인다. 실제로도 조밀한 부호는 아니지만, 부호화 및 복호화가 쉽다는
장점이 있다. 한편 해밍 부호를 비롯한 많은 부호가 통신 중에 발생할 수 있는 오류를 교정하는 데는 탁월하지만, 한 개의 비트가 첨가되거나
삭제되는 사소한(?) 오류에는 속수무책인 경우가 많다. 이런 단점을 보완하기 위해 피보나치 부호처럼 구분자를 사용하는 것이 알기 쉬운데, 특히
문자 기반의 문서의 전송 시 첨삭으로 인한 오류에 저항성이 높다. 뿐만 아니라, 사진이나 영상을 압축할 때 JPEG2000을
비롯한 상용 부호화 기법에 비해 피보나치 부호가 뒤지지 않는 압축률을 보인다는 실험 결과도 있다. 간단한(?) 게임에 얽힌 수학도 이렇게 응용될
수 있다는 사실! 수학은 엉뚱한 데서 나타나는 매력이 있다.
네이버캐스트


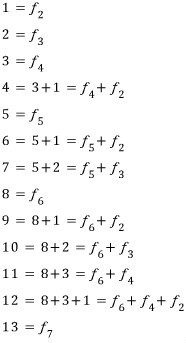
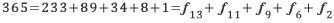
댓글 없음:
댓글 쓰기