두
정수가 주어지면 이 두 수의 공약수가 존재한다. 그런데 주어진 수가 정수가 아닌 경우에는 어떻게 될까? 존재한다면 구하는 방법을, 존재하지
않는다면 어떤 경우에 존재하지 않는지에 대해 살펴보자. 수학 용어이지만 수학이 아닌 일상 생활에서 가장 자주 사용되고 있는 용어중의 하나가
최대공약수가 아닌가 싶다. ‘최대공약수’가 일상 용어로 사용될 때는, 최대공약수라는 개념 보다는 용어에 내재된 이미지를 부각시켜 사용되는
듯하다. 뉴스를 보면 대립되는 양쪽의 의견을 조율해서 합의를 도출할 때 흔히 “최대공약수를 찾는데 노력했다”라는 표현을 흔히 나온다.
최대공약수는
비단 일상생활에서만 사용되는 것은 아니다. 다양한 과학적인 상황에서도 폭넓게 사용되고 있다. 예를 들어, 1923년 기본 전하와 광전효과에 대한
연구로 노벨 물리학상을 받은 로버트 밀리컨(Robert Millikan,
1868~1953)은 가장 작은 전하량인 기본 전하량 e의 크기를 구하기 위해 실시한 기름방울시험에서 최대공약수를 활용하였다.

|
|
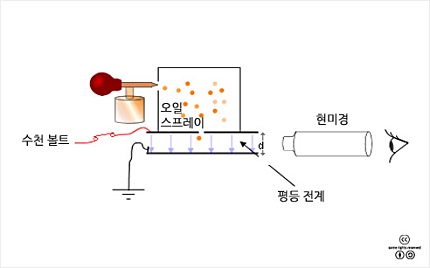
밀리컨은
이 실험에서 중력에 의해 내려가는 기름방울의 힘과 두 금속 전극 사이에 정지되어 있는 작은 기름 방울에 작용하는 힘 사이의 균형 상태를
측정하였다. 이러한 수백 번의 실험 끝에 기름방울에 있는 전하량의 크기들을 구하였다. 그런데, 모든 전하량의 크기는 전자가 가지는 기본
전하량(e)의 정수배가 되어야 한다는 사실로부터, 기본 전하량 e를 기름방울실험에서 얻은 전하량들의 최대공약수를 통해 얻는데 성공하였다.
공약수
개념
일반적으로
알고 있는 공약수에 대한 개념은 정수에 국한되어 있다. 하지만, 공약수 발생의 근원은 선분의 길이에 대한 공통 측도(공약수)에 있다. 동일한
개념이지만 다루는 대상에 따른 두 접근법에 대해 살펴보자. 먼저 공약수의 개념이다. 두 정수A, B가 주어져 있다.A가a의 정수배( k 1)이고, 동시에B가a의 정수배( k 2)가 될 때,a는 두 정수A와B의 공약수라고 한다. 즉, 아래를 만족하는
정수 k 1, k 2가 존재하면a는A, B의 공약수이다.
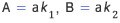
이러한a중에서
가장 큰 값을 최대공약수라고 부른다. 예를 들어, 두 정수 8과 12에 대해 생각해 보자. 아래가 성립하므로 2는 12와 8의
공약수이다.
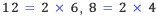
다음으로
공통 측도의 개념이다. 두 선분 AB와
선분CD가
아래와 같이 주어져 있다.

선분 AP의
길이(a)와 선분 CQ의
길이(a)가 같도록 점 P와 점 Q를 잡는다. 이 때, 선분 AB는a의 k 1배 이고, 동시에 선분 CD가a의 k 2배가 될 때,a는 두 선분의 공통 측도라고 한다. 즉,
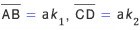
를
만족하는 정수 k 1, k 2가 존재하면a는 선분 AB와
선분 CD의
공통 측도(공약수)이다. 이러한a중에서 가장 큰 값을 최대 공통 측도(최대공약수)라고 부른다.
아래
그림과 같이 가로 120, 세로 72의 길이를 가지는 직사각형 모양의 바닥이 있다. 이 바닥에 정사각형 모양의 타일을 빈틈없이 붙이려고 한다.
이 때, 타일의 한 변의 길이a는 얼마인가?
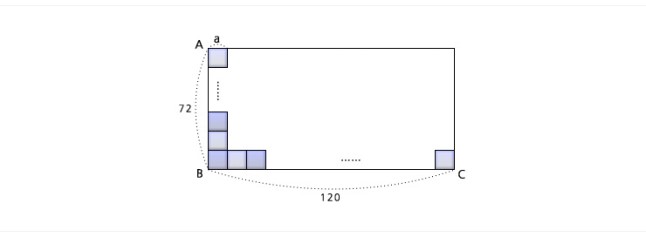
다음
식을 만족하는 정수 k 1, k 2가 존재하도록 정사각형의 한 변a를 결정하면 이 문제는 해결된다.
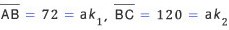
실제로
정사각형의 한 변의 길이로 가능한 값은a=1, 2, 3, 4, 6, 8, 12, 24 이다. 위의 예에서 알 수 있듯이 주어진 두 선분의 길이가
모두 정수(자연수) 값을 가진다면, 항상 1을 공통 측도로 가질 수 있으므로, 임의의 두 정수(자연수)는 항상 공통 측도를 가진다.
그런데
위의 정사각형 타일의 문제를 다시 보자. 만약 타일의 한 변의 길이가 a=1/2인 경우에는 어떻게 되겠는가? 주어진 식

을
만족시키는 정수 k 1, k 2가 존재하므로, a=1/2도 72와 120의 공통 측도임이 분명하다.
다시
밀리컨의 기름방울실험에 대해 생각해 보자. 밀리컨이 구한 전하량은 e=1.592×10-19C이었다. 즉,
기름방울실험에서 얻은 전하량들의 크기의 최대공약수로1.592×10-19를 얻은 것이다.이를
통해 볼 때, 유리수도 공약수(공통 측도)의 값으로 가능함을 알 수 있다.
고등
학교까지는 정수 값에 대한 공약수만을 학습하지만, 일상생활과 과학에서는 이것만으로 충분하지 않다. 임의의 두 유리수에 대한 공약수를 어떻게 구할
수 있는지에 대해 살펴 보자.아래와 같이 두 유리수가 주어져 있다. 만일 이 두 수의 공약수가 존재하려면 어떤 조건이 필요한자 살펴보자.
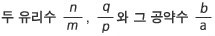
그러면,
다음을 만족하는 두 정수 k 1, k 2가 존재해야 한다.
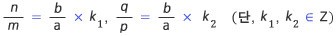
이로부터,
두 정수 k 1, k 2는 다음 조건을 만족한다.
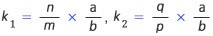
따라서, k 1, k 2가 정수이기 위해서는 a와 b는 다음 두 조건을 만족해야 한다.

그러므로, 두 유리수의 공약수는 다음과 같다.

이때,
최대공약수는 공약수 중에서 가장 큰 값이므로 아래와 같다.

이제,
구체적으로 주어진 두 유리수 5/2, 4/3의 최대공약수를 구해 보자.
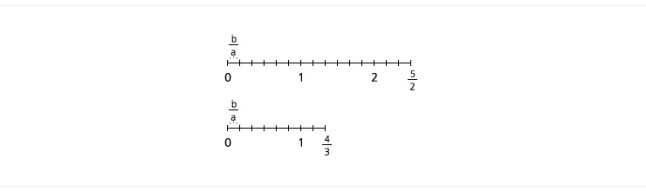
위의
그림을 통해 두 유리수 5/2, 4/3의 공약수로 1/6을 가짐을 직관적으로 알 수 있다. 실제로 아래와 같이 되므로 최대공약수는
1/6이다.

임의로
주어진 두 유리수는 반드시 최대 공통 측도(최대공약수)를 가진다. 그렇다면 무리수는 어떻게 될까? 이에 대한 의문을 던진 최초의 사람은 고대
그리스인들이었고, 이 문제에 대한 해답을 찾은 사람은 피타고라스 학파였다. 처음에 피타고라스 학파의 사람들은 최대 공통 측도가 있다는 믿음을
가지고 있었지만, 곧 거짓임이 밝혔다. 그 대표적인 예가 1과 √2사이에는 최대공약수가 존재하지 않는다는 것이다. 즉, 공통측도에 대해서
정리하면 아래와 같다.

피타고라스
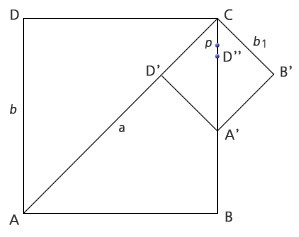
학파의 방법으로 이 문제에 대해 고찰해 보면 이렇다. 두 실수 1과 √2를 도형을 통해 볼 수 있는 가장 간단한 방법은 한 변의 길이가 1인
정사각형에서 한 변과 그 대각선이다. 그림에서 선분 AB가
1이고, 선분 AC가
√2이다. 이 두 수 사이에 최대 공통 측도(최대공약수)가 존재하지 않는 것은 다음과 같이 증명한다.
(증명)
증명을 위해 AB와 AC가
최대 공통 측도를 가진다고 가정 해 보자. 그리고, 그 값을 CP라고
가정하자. 위의 정사각형 ABCD에서
대각선의 길이를a, 정사각형의 한 변의 길이를b라고 하고, 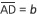 와 같은 선분
와 같은 선분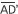 을 작도하고, 선분
을 작도하고, 선분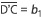 에 정사각형 A'B'CD'을
작도하자. 정사각형 A'B'CD'의
대각선에
에 정사각형 A'B'CD'을
작도하자. 정사각형 A'B'CD'의
대각선에 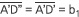 이 되도록 D''을
잡자.
이 되도록 D''을
잡자.
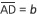 와 같은 선분
와 같은 선분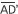 을 작도하고, 선분
을 작도하고, 선분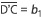 에 정사각형 A'B'CD'을
작도하자. 정사각형 A'B'CD'의
대각선에
에 정사각형 A'B'CD'을
작도하자. 정사각형 A'B'CD'의
대각선에 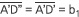 이 되도록 D''을
잡자.
이 되도록 D''을
잡자.
이
때, △ABD'이
이등변삼각형이고, ∠ABA'
과 ∠A'D'A가 직각이므로∠A'BD'=∠A'D'B가
성립한다. 따라서, △A'BD'은
이등변삼각형이고, 가 된다.
가 된다.
 가 된다.
가 된다.
그러므로, AC와 BC가 CP의
배수이기 때문에, AC-BC=CD'도 BC-A'B=CA'도 CP의
배수이다. 즉, 새로운 작은 정사각형에서의 한 변의 길이(A'D')와 대각선의 길이(CA')의
최대 공통 측도는 선분 CP이다.
이와 같은 과정은 무한히 계속 반복될 수 있으므로, 언젠가는 최대 공통 측도(CP)보다
더 작은 값을 한 변의 길이로 가지는 정사각형을 얻게 된다. 그런데, 이 정사각형에서도 한 변의 길이는 선분 CP의
정수배가 되어야 하는데, 이것은 모순이다.
이러한
모순의 원인은 최대 공통 측도가 존재한다는 가정이 잘못되었기 때문에 생긴 것이므로 결국 1과 √2사이에는 최대 공통 측도가 존재할 수 없다.
(증명 끝)
- 네이버캐스트

댓글 없음:
댓글 쓰기