평균도 다양하다

시속 100km로 한 시간을 달려야 하는 길을 왕복하려고 한다. 갈 때 차량이 많아 시속 80km의 속력으로 달려야 하였다. 그렇다면 나머지 절반을 어느 정도 속력으로 달려야 왕복 두 시간이 될까? 시속 120km? 이상하게도 시속 120km로 달려서는 왕복 시간이 두 시간을 넘게 된다. 왜 그럴까?

속력에는 조화평균

언뜻 생각하기에는 80과 120의 평균이 100이니, 되돌아 올 때 시속 120km로 달리면 충분한 것 같은데, 왜 늦어지는 걸까? 앞서 이야기한 상황에서 시속 100km로 한 시간 동안 달리는 거리는 100km. 이 거리를 시속 80km로 달릴 때 걸리는 시간은 100/80 = 5/4시간. 다시 100km를 시속 120km로 달리면, 100/120 = 5/6시간이 걸리니까, 전체 소요 시간은 5/4 + 5/6 = 25/12시간이 된다. 따라서 1/12시간, 즉 5분이 더 걸린다.

두 시간 만에 왕복하려면 되돌아 올 때 100km를 3/4시간 동안 달려야 하니까, 속력은 시속 100/(3/4) = 133.3km가 되어야 한다. 당연히 시속 120km로 달려서는 늦을 수밖에 없다. 이처럼 평균 속력을 계산할 때는, 다음처럼 보통 평균을 내는 방식을 이용해서는 안 된다.

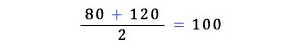
시속 80km와 시속 133.3km의 평균 속력을 구할 때는 다음과 같이 계산해야 한다.

이와 같은 평균을 조화평균(harmonic mean)이라 한다. 이 방법으로 시속 80km와 시속 120km의 평균 속력을 계산하면 다음과 같다.

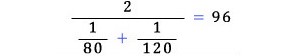
즉, 시속 80km와 시속 120km로 같은 거리를 오가면, 평균 속력은 시속 100km가 아니라 시속 96km밖에 되지 않는다.

흔히 보는 산술평균

많은 양의 자료를 다룰 때, 전체적인 양상을 하나의 수로 나타내면 편리한 경우가 많다. 이때 흔히 사용하는 개념이 바로 평균이다. 우리가 보통 사용하는 평균은 산술평균(arithmetic mean)으로, 한 반의 시험 성적을 전부 더한 다음 학생 수로 나눈 반평균도 그 한 예이다. 중학생의 평균 키니, 평균 몸무게니 하는 것도 모두 산술평균을 이용하여 구하게 된다. 그런데 앞서 평균속력의 예에서 보듯, 경우에 따라 전혀 다른 방법으로 평균을 구해야 하는 경우가 있다.

경제성장률에는 기하평균

산술평균, 조화평균과 함께 자주 볼 수 있는 평균으로는 기하평균(geometric mean)을 들 수 있다. 이것은 특히 경제성장률이나 인구증가율을 나타낼 때 흔히 볼 수 있다. 예를 들어, 어떤 나라의 경제 규모가 x 달러였다고 하자. 이 나라의 경제 규모가 1년 동안 2배로 커져 2x 달러가 된다면 경제성장률은 100%가 된다. 만약 그 다음 1년 동안은 경제를 말아먹어서 경제 규모가 1/2배인 x 달러로 쪼그라든다면, 경제성장률은 -50%가 된다. 이때 2년 동안의 경제성장률을 1년 단위로 평균을 낸다면 어떻게 하는 게 합리적일까? 그냥 2배와 1/2배의 산술평균을 구하여 1.25배라고 하면 어떨까? 원래의 경제 규모로 되돌아갔으니, 경제가 성장한 것이 없는데도 1.25배라고 하는 것은 아무래도 부적절하다. 사람들이 산술평균에 익숙하기 때문에, 이처럼 실제로는 성장한 것이 없는데도, 적절하지 않은 평균을 이용하여 사람들을 속이는 경우가 많다. 은행에서 기하평균이 아닌 산술평균을 이용하여 이자율을 보여주거나 하는 것도 이런 거짓말 -- 좋게 말해 상술 -- 가운데 하나이며, 경제 관련 정부 부처의 대변인은 특히 이 방면의 전문가들이다. 이 경우는 다음과 같이 생각하는 것이 훨씬 합리적이다.

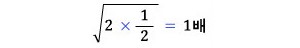
이렇게 자료들을 곱한 다음 그 거듭제곱근을 구한 것을 기하평균이라 한다.

세상은 여섯사람으로 연결되어 있다, 중앙값

모르는 두 사람도 여섯 명만 거치면 연결된다는 속설은 미국의 사회심리학자 스탠리 밀그램(Stanley Milgram, 1933~1984)의 우편물 전달 실험으로 유명해졌다. 이 실험은 전혀 다른 지역에 살고 있는 모르는 사람에게 우편물을 전달하려면 몇 단계를 거쳐야 하는지를 조사한 것으로, 실험 결과 중앙값이 5.5명으로 나왔다. 밀그램이 보통의 산술평균을 쓰지 않고 중앙값을 쓴 것은, 하나의 값이 산술평균에 지나치게 큰 영향을 미칠 수 있기 때문이다. 예를 들어, 실험에 참가한 사람이 모두 우편물을 한 두 번 만에 전달하였지만, 딱 한 사람만은 수 십 단계를 거쳐야 했다면, 산술평균의 결과는 너무 큰 값이 나온다. 이런 이유로 실험의 결과를 크기 순으로 나열한 다음 한 가운데 오는 값을 구한 것이고, 이것을 중앙값이라 한다. 이와 비슷한 현상은 빈부격차가 큰 나라의 국민소득을 계산한 때도 쉽게 볼 수 있다. 1인당 국민소득은 꽤 높은데, 국민의 90%는 생계를 걱정해야 하는 빈민층인 나라를 생각하면 되겠다.

다른 평균들 - 최빈값, 사분평균

이처럼 극단적인 값들 때문에 평균이 왜곡될 때 사용할 수 있는 평균값으로는 중앙값 외에도 가장 빈도가 높은 값인 최빈값, 낮은 쪽과 높은 쪽 자료의 1/4씩을 제외하고 평균을 구하는 사분평균 등이 있다. 체조 경기의 점수를 매길 때, 최저점수와 최고점수를 빼고 평균을 구하는 것도 비슷하다 할 수 있다.

체조경기에서 최초로 10점 만점을 받은 나디아 코마네치. 심판들의 10점을 평균하면 1점이 된다고 생각한 것일까? 당시의 전광판으로는 10.00을 표시할 수 없어서 1.00으로 나타내었다

평균을 구하는 방법은 필요에 따라 다양하다

결국 평균을 구하는 방법은 우리의 목적과 필요에 따라 얼마든지 다양하며, 전혀 새로운 종류의 평균을 생각해야 하는 경우도 있다. 3가지 사례를 제시하니 참고하기 바란다.

전류의 실효값이란?

평균이라는 것이 필요에 따라 자료를 정리하여 나타내는 값이므로, 사실 앞서 설명한 평균들 외에도 수없이 많은, 사실상 무한히 많은 평균을 생각할 수 있다. 예를 들어, 전기공학에서 교류의 전류나 전압의 크기를 나타낼 때 쓰이는 실효값(Root Mean Square, RMS)도 자주 쓰이는 평균의 한 종류이다. 220V라고 할 때의 220이 바로 실효값이다. 이 값은 다음과 같이 구한다. 글자 그대로 제곱(square)하고 평균(mean)을 구한 다음 제곱근(root)을 구한다.

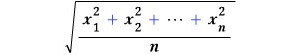
실효값을 이런 식으로 정하는 이유는 전력이 전류의 제곱을 이용하여 표현되기 때문에, 단순히 산술평균을 구하는 것보다 훨씬 쓸모가 있기 때문이다. 게다가 교류의 전류에 대한 산술평균 값을 곧이곧대로 구한다면 0이 되어 아무 의미가 없다.

색종이의 넓이에 관심이 있다면?

다양한 크기의 색종이의 평균은?

실효값은 다음과 같은 예를 생각할 수도 있다. 여러 장의 (정사각형 모양) 색종이가 주어졌을 때, 그 평균을 얼마로 생각하면 좋을까?

물론 색종이의 한 변의 길이에 대한 산술평균을 구할 수도 있지만, 만약 우리가 색종이의 넓이에 더 관심이 있다면, 넓이(square)의 평균(mean)을 구한 다음 그 제곱근(root)을 평균으로 생각할 수도 있다.

이렇게 구한 평균 길이가 주어지면 한 변의 길이가 대략 얼마인지도 알 수 있으면서, 그 값을 제곱하면 평균 넓이도 바로 알 수 있다.

다양한 크기의 주사위의 평균은?

정육면체에 부피에 관심이 있다면?

같은 생각을 정육면체 모양에 대해 적용한다면, 단순히 정육면체의 한 변의 길이에 관심이 있을 때는 그냥 산술평균을 구하면 되고, 정육면체의 겉넓이에 관심이 있다면 실효값(RMS)과 같은 것을 계산하면 된다. 만약 정육면체의 부피에 관심이 있다면?

이 경우는 정육면체의 한 변의 길이를 세제곱한 다음 평균을 구하고 다시 세제곱근을 구하면 된다.

우리가 자주 쓰지 않을 뿐이지, 이 또한 훌륭한 평균이다.

네이버캐스트