비누막에서 ‘어떤 경계가 주어졌을 때에 경계를 잇는 최소 면적의 곡면’인 ‘극소곡면(minimal surface)’ 발견할 수 있어
⊙ 2개, 혹은 3개의 비눗방울이 만날 때의 각도는 항상 120°
⊙ 비눗방울이 모여서 만나는 경계면은 가장 작은 면적을 가져
⊙ 2개, 혹은 3개의 비눗방울이 만날 때의 각도는 항상 120°
⊙ 비눗방울이 모여서 만나는 경계면은 가장 작은 면적을 가져

- 비눗방울은 자연에서 찾아볼 수 있는 ‘가성비’ 높은 물체 중 하나다.
우리는 살면서 많은 것을 가지고 싶고, 가장 좋은 것을 가지고 싶어 한다. 가져다 쓸 자원이 많으면 상관이 없지만 대부분의 사람은 돈이나 시간 등의 한계가 있어 그 욕구를 다 채울 수 없다. 그래서 항상 사용할 수 있는 자원의 범위 내에서 가장 많은 효과를 볼 수 있는 최적의 방법, 이른바 ‘가성비’를 추구한다.
비눗방울은 자연에서 찾아볼 수 있는 ‘가성비’ 높은 물체 중 하나이다. 물에 적당량 비누를 풀어 빨대 등을 이용하여 불어내면 동그란 비눗방울이 만들어진다. 비눗방울은 왜 동그란 모양을 가지는 걸까? 물은 분자끼리 서로 끌어당기는 힘이 강해서 액체의 표면을 작게 하려는 힘인 표면장력(張力)이 강하다. 많은 양이 모였을 때는 지구의 중력 때문에 흘러내리지만 소량의 물, 혹은 무중력 공간에서는 표면장력으로 인해 동그란 형태를 가진다. 이는 같은 부피(양)의 물이 가질 수 있는 가장 작은 표면적의 모양이 구(球)의 형태이기 때문이다.
하지만 물로는 비눗방울과 같이 내부가 비어 있는 방울을 만들기 힘들다. 표면장력이 너무 강해서 그 안을 공기가 비집고 들어가기 힘들기 때문이다. 하지만 물에 비누를 풀면 표면장력이 약해져 빨대에 공기를 불어 넣는 것으로 비눗방울을 만들 수 있게 된다. 약해지긴 했지만 표면장력을 가지고 있는 비눗방울은 내부에 담고 있는 기체를 비눗물이라는 한정된 자원으로 감싸고 있기에 부피 대비 면적이 가장 작은 형태인 구의 형태를 유지하는 것이다.
비눗방울의 경계면, 비누막
비눗방울 공연장에서는 큰 비눗방울을 만들기 위해 철사 등으로 만든 고리를 이용한다. 비눗방울을 만들기 위해 고리를 비눗물에 적시고 꺼내면 고리 사이에 비누막이 생긴다. 벨기에의 물리학자 플라토(Joseph Plateau·1801~1883)는 다양한 형태의 철사 모형을 비눗물에 적셨을 때에 생기는 비누막에 대해 관심을 가졌다.
철사 모형에는 항상 비누막이 생긴다. 이때 생기는 비누막은 항상 면적을 최소화하는 형태로 모양을 이룬다. 쉬운 예로 평평한 고리에 생기는 비누막은 고리 내부를 채우는 평평한 모양이며, 볼록하거나 오목한 모양은 생기지 않는 것을 바로 떠올릴 수 있을 것이다.
플라토가 비누막에서 발견한 비누막의 성질과 같이, 어떤 경계가 주어졌을 때에 경계를 잇는 최소 면적의 곡면을 수학적으로 ‘극소곡면(minimal surface)’이라 한다. 플라토가 관찰한 비누막이 모든 모형에서 항상 존재하는지에 대한 여부는 많은 시일 동안 밝혀지지 않았지만 1930년에 들어 더글러스와 라도에 의해 증명되었다. 이 공로로 더글러스는 1936년 수학계의 노벨상이라는 필즈상을 수여받았다.
극소곡면
사실 극소곡면에 대한 것은 플라토 이전부터 연구되었다. ‘플라토의 문제’라고 불리는 극소곡면에 대한 문제는 프랑스 수학자 라그랑주(Lagrange·1736~1813)로부터 시작되었는데, 플라토의 비누막 실험으로 인해 이름을 빼앗긴 꼴이다.
극소곡면의 문제에서 중요한 것은 ‘어떤’ 경계가 주어졌을 때, 그 경계를 잇는 곡면이 ‘어떤 모양’일 때 가장 면적이 작을 것이냐이다. 그렇다면 위 사진과 같이 두 개의 고리가 있고 두 고리를 이어주는 비누막은 어떨까?
고리의 위치에 따라 다르겠지만 두 고리가 서로 포개어지는 위치에 있으며, 높이만 다른 경우에 대해서는 라그랑주와 동시대의 수학자 레온하르트 오일러가 이미 밝혀냈다. 오일러가 밝혀낸 극소곡면의 형태는 ‘현수면(catenoid)’으로, 두 고리의 높이에 따라 휘어지는 정도는 다르지만 하나의 식으로 나타낼 수 있는 곡면을 찾아냈다. 오일러는 현수면 이외에도 ‘나선곡면(helicoid)’을 극소곡면의 한 예로 보여주었다. 이는 좁은 공간에서 위층과 아래층을 오갈 수 있도록 만든 나선계단에서 볼 수 있다. 중세 유럽 건축물에서 찾아볼 수 있는 나선형 계단은 수학으로 증명하기 이전에도 가장 적은 비용으로 만들며, 자연에서 보는 아름다움을 느낄 수 있는 형태라고 생각했는지도 모른다.
오일러의 업적 이후 극소곡면의 다른 예가 좀처럼 등장하지 않았는데, 200여 년이 지난 1982년에 와서 브라질의 대학원생 코스타(Costa)가 원형 고리가 3개인 극소곡면을 선보임으로써 현수면과 나선곡면 이외의 많은 극소곡면을 찾아내는 데 도움을 주었다.
비누막이 알려주는 최단거리
유명한 프랑스 수학자 페르마(Pierre de Fermat·1607~1665)는 평면 위에 3개의 점이 주어졌을 때, 3개의 점에 이르는 길이의 합이 가장 짧게 되는 점을 구하는 문제를 제시했다.
이 문제를 조금 바꾸어보면 ‘주어진 도시 N개를 모두 연결되게 하는 가장 짧은 경로는 어떻게 구할 수 있을까?’라는 문제로 생각해 볼 수 있다. 이 문제는 비누막이 최소한의 면적으로 이루어지려 하는 성질을 이용하면 쉽게 해결이 된다. 점이 3개인 경우 이탈리아의 토리첼리(Evangelista Torricelli·1608~1647)는 3개의 점을 지나는 원을 이용하여 해결을 했는데, 3개의 비누막을 관찰해 보면 수학적 결과와 같다는 것을 알 수 있다. 점이 3개가 아닌 경우에도 비누막을 이용해 이 모습을 확인할 수 있는데, 다음은 정사각형과 같이 점이 4개인 경우의 한 예이다.
위와 같이 직사각형의 4개의 점이 있다면 직사각형의 두 대각선이 교차하는 점으로부터 4개의 점을 연결하는 것이 길이가 가장 짧은 것이라는 생각이 직관적으로 들게 될 것이다. 하지만 비누막이 생길 수 있도록 얇은 기둥을 세워 확인을 해보면, 위와 같이 모든 비누막이 서로 120°로 만나는 것을 볼 수 있고, 실제로 계산을 해보아도 가장 짧다는 것을 알 수 있다.
비눗방울이 서로 만날 때
위의 실험에서 세 개의 비누막이 서로 만날 때, 그 각도가 120°가 되는 것을 확인할 수 있었다. 이는 비눗방울로 실험을 한 플라토가 관찰한 사실 중 하나이며 심지어 그는 네 개의 비눗방울이 한 점에서 만날 때는 비누막들이 서로 109.5°를 이룬다는 것도 관찰했다.
과연 이것은 항상 그러할까? 혹시 비슷한 크기의 거품들에만 해당되는 것이 아닐까? 아직 모든 경우에 증명이 되진 않았지만 적어도 두 개의 비눗방울이 만날 때는 항상 120°를 이룬다는 것이 2002년 미국의 수학자 프랭크(Frank Morgan)에 의해 증명되었다.
위와 같이 크기가 매우 차이가 나는 두 비눗방울이 만날 때는 작은 방울이 큰 방울을 침투하듯 내부로 들어간 것을 볼 수 있다. 작은 비눗방울이 원형을 유지하는 것보다 큰 방울 내부로 들어가면서 면적을 보다 최소화할 수 있기 때문이다. 이 최소화된 비눗방울의 면적에서도 두 비눗방울의 각각의 곡면과 경계면이 모두 동그란 구면의 일부분임은 변하지 않는다.
두 개의 비눗방울이 위와 같은 모양이 아니라 하나의 비눗방울을 다른 비눗방울이 도넛처럼 감싸고 있는 모양이 있을 수도 있다. 하지만 비눗방울이 위와 같이 일반적으로 만나는 모양일 때 가장 면적이 작으며, 그렇기에 두 비눗방울이 만나는 각도는 항상 120°가 된다.
비눗방울이 세 개 이상일 때는 아직 모든 경우에 대한 증명이 되지 않았다. 따라서 플라토의 관찰에 따른 결과는 추측이 될 뿐이다. 하지만 자연이 보여주는 최적의 모양은 현재까지의 결과로 보았을 때, 수학적으로 매우 아름답다는 것을 말해주고 있어 추측이 사실일 가능성이 높다고 생각된다.
비눗방울 원리 이용해 만든 뮌헨올림픽스타디움
비눗방울이 모여서 만나는 경계면은 가장 작은 면적을 가진다는 것은 실험적으로 입증된 결과이다. 이를 실생활에 사용한 곳이 있다. 1972년 독일 올림픽이 열린 뮌헨올림픽스타디움이 바로 그 예이다. 뮌헨 경기장의 지붕은 중간중간 움푹 파인 곳이 있는데, 바로 비눗방울들이 서로 맞붙은 경계면을 따라 만들었기 때문이다. 건축 설계자 프라이 오토(Frei Otto)와 군터 베니시(Günter Behnisch)는 뮌헨 경기장의 축소된 형태를 만든 뒤, 비눗방울이 어떻게 만나는지를 관찰한 뒤 건축물을 지은 것이다. 건축을 할 때, 가장 중요한 건축의 안정성과 비용적인 측면이 자연이 보여주는 최적의 형태로 검증이 된 것이다. 여기에 자연이 선사하는 아름다움이 더해졌으니 수학적, 예술적, 경제적 측면에서 찬사받을 만한 건축물이 아닌가 싶다.⊙
비눗방울은 자연에서 찾아볼 수 있는 ‘가성비’ 높은 물체 중 하나이다. 물에 적당량 비누를 풀어 빨대 등을 이용하여 불어내면 동그란 비눗방울이 만들어진다. 비눗방울은 왜 동그란 모양을 가지는 걸까? 물은 분자끼리 서로 끌어당기는 힘이 강해서 액체의 표면을 작게 하려는 힘인 표면장력(張力)이 강하다. 많은 양이 모였을 때는 지구의 중력 때문에 흘러내리지만 소량의 물, 혹은 무중력 공간에서는 표면장력으로 인해 동그란 형태를 가진다. 이는 같은 부피(양)의 물이 가질 수 있는 가장 작은 표면적의 모양이 구(球)의 형태이기 때문이다.
하지만 물로는 비눗방울과 같이 내부가 비어 있는 방울을 만들기 힘들다. 표면장력이 너무 강해서 그 안을 공기가 비집고 들어가기 힘들기 때문이다. 하지만 물에 비누를 풀면 표면장력이 약해져 빨대에 공기를 불어 넣는 것으로 비눗방울을 만들 수 있게 된다. 약해지긴 했지만 표면장력을 가지고 있는 비눗방울은 내부에 담고 있는 기체를 비눗물이라는 한정된 자원으로 감싸고 있기에 부피 대비 면적이 가장 작은 형태인 구의 형태를 유지하는 것이다.
비눗방울의 경계면, 비누막
 |
| 물리학자 플라토. |
철사 모형에는 항상 비누막이 생긴다. 이때 생기는 비누막은 항상 면적을 최소화하는 형태로 모양을 이룬다. 쉬운 예로 평평한 고리에 생기는 비누막은 고리 내부를 채우는 평평한 모양이며, 볼록하거나 오목한 모양은 생기지 않는 것을 바로 떠올릴 수 있을 것이다.
플라토가 비누막에서 발견한 비누막의 성질과 같이, 어떤 경계가 주어졌을 때에 경계를 잇는 최소 면적의 곡면을 수학적으로 ‘극소곡면(minimal surface)’이라 한다. 플라토가 관찰한 비누막이 모든 모형에서 항상 존재하는지에 대한 여부는 많은 시일 동안 밝혀지지 않았지만 1930년에 들어 더글러스와 라도에 의해 증명되었다. 이 공로로 더글러스는 1936년 수학계의 노벨상이라는 필즈상을 수여받았다.
극소곡면
 |
| 왼쪽부터 현수면, 나선곡면, 코스타의 극소곡면. |
극소곡면의 문제에서 중요한 것은 ‘어떤’ 경계가 주어졌을 때, 그 경계를 잇는 곡면이 ‘어떤 모양’일 때 가장 면적이 작을 것이냐이다. 그렇다면 위 사진과 같이 두 개의 고리가 있고 두 고리를 이어주는 비누막은 어떨까?
고리의 위치에 따라 다르겠지만 두 고리가 서로 포개어지는 위치에 있으며, 높이만 다른 경우에 대해서는 라그랑주와 동시대의 수학자 레온하르트 오일러가 이미 밝혀냈다. 오일러가 밝혀낸 극소곡면의 형태는 ‘현수면(catenoid)’으로, 두 고리의 높이에 따라 휘어지는 정도는 다르지만 하나의 식으로 나타낼 수 있는 곡면을 찾아냈다. 오일러는 현수면 이외에도 ‘나선곡면(helicoid)’을 극소곡면의 한 예로 보여주었다. 이는 좁은 공간에서 위층과 아래층을 오갈 수 있도록 만든 나선계단에서 볼 수 있다. 중세 유럽 건축물에서 찾아볼 수 있는 나선형 계단은 수학으로 증명하기 이전에도 가장 적은 비용으로 만들며, 자연에서 보는 아름다움을 느낄 수 있는 형태라고 생각했는지도 모른다.
오일러의 업적 이후 극소곡면의 다른 예가 좀처럼 등장하지 않았는데, 200여 년이 지난 1982년에 와서 브라질의 대학원생 코스타(Costa)가 원형 고리가 3개인 극소곡면을 선보임으로써 현수면과 나선곡면 이외의 많은 극소곡면을 찾아내는 데 도움을 주었다.
비누막이 알려주는 최단거리
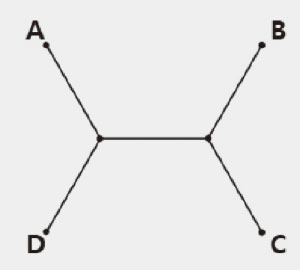 |
| 4개의 점이 주어졌을 때 최소의 길이. |
이 문제를 조금 바꾸어보면 ‘주어진 도시 N개를 모두 연결되게 하는 가장 짧은 경로는 어떻게 구할 수 있을까?’라는 문제로 생각해 볼 수 있다. 이 문제는 비누막이 최소한의 면적으로 이루어지려 하는 성질을 이용하면 쉽게 해결이 된다. 점이 3개인 경우 이탈리아의 토리첼리(Evangelista Torricelli·1608~1647)는 3개의 점을 지나는 원을 이용하여 해결을 했는데, 3개의 비누막을 관찰해 보면 수학적 결과와 같다는 것을 알 수 있다. 점이 3개가 아닌 경우에도 비누막을 이용해 이 모습을 확인할 수 있는데, 다음은 정사각형과 같이 점이 4개인 경우의 한 예이다.
위와 같이 직사각형의 4개의 점이 있다면 직사각형의 두 대각선이 교차하는 점으로부터 4개의 점을 연결하는 것이 길이가 가장 짧은 것이라는 생각이 직관적으로 들게 될 것이다. 하지만 비누막이 생길 수 있도록 얇은 기둥을 세워 확인을 해보면, 위와 같이 모든 비누막이 서로 120°로 만나는 것을 볼 수 있고, 실제로 계산을 해보아도 가장 짧다는 것을 알 수 있다.
비눗방울이 서로 만날 때
위의 실험에서 세 개의 비누막이 서로 만날 때, 그 각도가 120°가 되는 것을 확인할 수 있었다. 이는 비눗방울로 실험을 한 플라토가 관찰한 사실 중 하나이며 심지어 그는 네 개의 비눗방울이 한 점에서 만날 때는 비누막들이 서로 109.5°를 이룬다는 것도 관찰했다.
과연 이것은 항상 그러할까? 혹시 비슷한 크기의 거품들에만 해당되는 것이 아닐까? 아직 모든 경우에 증명이 되진 않았지만 적어도 두 개의 비눗방울이 만날 때는 항상 120°를 이룬다는 것이 2002년 미국의 수학자 프랭크(Frank Morgan)에 의해 증명되었다.
위와 같이 크기가 매우 차이가 나는 두 비눗방울이 만날 때는 작은 방울이 큰 방울을 침투하듯 내부로 들어간 것을 볼 수 있다. 작은 비눗방울이 원형을 유지하는 것보다 큰 방울 내부로 들어가면서 면적을 보다 최소화할 수 있기 때문이다. 이 최소화된 비눗방울의 면적에서도 두 비눗방울의 각각의 곡면과 경계면이 모두 동그란 구면의 일부분임은 변하지 않는다.
두 개의 비눗방울이 위와 같은 모양이 아니라 하나의 비눗방울을 다른 비눗방울이 도넛처럼 감싸고 있는 모양이 있을 수도 있다. 하지만 비눗방울이 위와 같이 일반적으로 만나는 모양일 때 가장 면적이 작으며, 그렇기에 두 비눗방울이 만나는 각도는 항상 120°가 된다.
비눗방울이 세 개 이상일 때는 아직 모든 경우에 대한 증명이 되지 않았다. 따라서 플라토의 관찰에 따른 결과는 추측이 될 뿐이다. 하지만 자연이 보여주는 최적의 모양은 현재까지의 결과로 보았을 때, 수학적으로 매우 아름답다는 것을 말해주고 있어 추측이 사실일 가능성이 높다고 생각된다.
비눗방울 원리 이용해 만든 뮌헨올림픽스타디움
 |
| 비눗방울의 만남에서 모티브를 얻은 뮌헨올림픽스타디움. |
월간조선
댓글 없음:
댓글 쓰기