반드시 순서를 지켜야 하는 일을 정리한 후 동시에 할 수 있는 일들을 찾는 것이 관건
⊙ 출발점과 종착점이 같은 경우는 ‘해밀턴 순환로’ 이론을 적용하면 세계여행 경로 계획할 수 있어
⊙ ‘빠른 길 찾기’ 앱 등에 적용
⊙ 출발점과 종착점이 같은 경우는 ‘해밀턴 순환로’ 이론을 적용하면 세계여행 경로 계획할 수 있어
⊙ ‘빠른 길 찾기’ 앱 등에 적용
한국은 유난히 빠른 것에 열광한다. 어떠한 상품을 예정보다 빨리 갖기 위해 더 비싼 가격을 주고 구입하기도 하고, 빠른 길을 찾아 가기 위해 실시간 교통정보가 반영된 내비게이션을 항상 켜고 운전하는 운전자도 많다. 또한 “최대한 빨리하겠습니다”라는 말은 회사에서 업무 할 때도 가게에서 상품을 준비할 때도 아주 빈번하게 사용한다. 여기서 ‘빠름’은 단순히 정말 어떤 것을 하는 데 걸리는 시간이 짧은 것을 의미하기도 하지만, 후자의 경우는 어떠한 일이 효율적으로 진행되는 것을 의미하기도 한다. 이번 글에서는 빠른 일 처리와 효율적인 시간 활용을 위해 사용하는 수학적 사고에 대해 살펴보려 한다.
효율적 생산을 위해서 - 최적 계획법
약 2년 전 한 감자칩이 품귀현상을 불러일으키며 폭발적인 인기를 누렸다. 시중에서 구하기가 매우 어려웠는데 ‘제조업체가 일부러 생산량을 조절하는 것이 아닌가’ 하는 소문까지 돌았다. 실제로 감자칩 제조 회사는 공장을 24시간 풀가동했을 뿐만 아니라 분명 가장 효율적인 방법으로 감자칩을 만들었을 것이다.
여기서 효율적인 방법이란 무엇일까? 하루 24시간 안에 보다 더 많은 과자를 만들어 내는 방법이 효율적인 방법일 것이다. 이처럼 짧은 시간 등과 같이 주어진 제약 조건하에서 효율을 극대화할 수 있게 하는 계획법을 ‘최적 계획법’이라고 한다.
다음 예를 보면서 최적 계획법에 대해 알아보자.
[예] 이해하기 쉽게 감자칩 한 봉지를 만드는 방법을 예로 살펴보자.
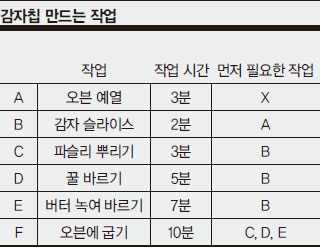
작업 방법을 참고하여 감자칩을 만들 때, A부터 F까지 순서대로 한다면 과자를 만드는 데 걸리는 시간은 총 3+2+3+5+7+10=30분이 걸린다. 이보다 짧은 시간에 감자칩을 만들 수는 없을까? 최적 계획을 세우기 위해서는 많은 것을 고려해야 하지만 가장 중요하게 고려되는 조건은 바로 시간이다. 그렇다면 시간을 단축하기 위해서는 어떻게 해야 할까? 우선, 반드시 순서를 지켜야 하는 일을 정리한다. 그런 후에 동시에 할 수 있는 일들을 찾는다. 이를 기억한 채로 다시 감자칩 만드는 작업으로 돌아가 보자.
A~F의 작업 중 일의 순서에 따라 그림으로 나타내면 다음과 같다.
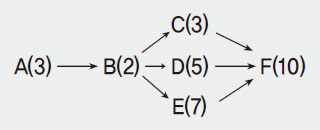
그림 ( )의 숫자는 걸리는 시간을 의미한다.
즉 작업 C, D, F는 동시에 해도 된다. 따라서 작업하는 데 걸리는 최소 시간은 동시에 해도 되는 작업 중 가장 많은 시간을 소요하는 작업을 지나는 경로의 시간을 합하면 되므로 3+2+7+10=22분이 된다.
우리는 사실 위와 같은 최적 계획법을 빈번하게 사용하고 있다. 매일 저녁 아내가 최대한 빨리 따끈하고 맛있는 저녁상을 차려낼 때도 최적 계획법이 사용될 수 있으며, 업무를 할 때도 알게 모르게 최적 계획법에 맞게 효율적인 업무를 하고 있을 것이다.
총알배송을 위한 경로 - 해밀턴 순환로
‘주문이 완료되었습니다. 주문하신 상품은 내일 바로 받아보실 수 있습니다.’
평일의 경우 밤 10시 전에 주문한 상품은 다음날 바로 받아볼 수 있다. 배송의 속도 경쟁이 치열한 요즘 총알배송, 로켓배송, 스마트배송 등 이른바 빠른 배송 시스템은 온라인 상품 판매 업체들에 빠져서는 안 될 마케팅 서비스 중 하나로 자리 잡았다. 적은 인력으로 최대한 빨리 배송을 하기 위해서 갔던 길을 다시 돌지 않는 최적 경로를 찾아 배송을 해야 한다. 다음의 경우를 생각해 보자.
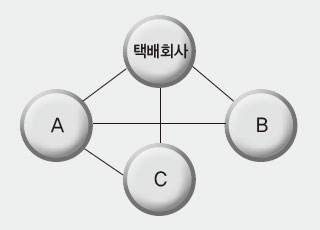
[예] 택배회사를 출발하여 A, B, C 세 곳을 모두 들러 상품을 배달하고 다시 택배회사로 돌아올 때 가장 효율적인 경로는 어떤 경로인지 생각해 보자. [택배회사 → B → A → C → 택배회사] 이 경로가 왔던 길을 다시 되돌아가지 않는 가장 효율적인 경로가 될 것이다. 단순한 예를 살펴봤지만 이는 그래프 이론 중 최적화 이론의 대표적인 예이다. 이러한 경로를 ‘해밀턴 경로’라고 하는데, 연결된 그래프로 나타낸 경로 중 모든 꼭짓점을 오직 한 번씩만 지나는 경로를 말한다. 해밀턴 경로 중에 출발점과 종착점이 같은 경우는 ‘해밀턴 순환로’라고 한다. 이 해밀턴 경로 이론을 적용할 수 있는 적절한 상황은 세계여행 경로를 계획할 때이다.
효율적인 세계일주 경로
세계일주 하는 사람들은 대개 저렴한 비용으로 가장 효율적으로 이동할 수 있는 경로를 찾아 여행 계획을 세운다. 이때 반드시 지켜야 하는 조건은 아래 두 가지이다.
1) 서울을 출발하여 서울로 다시 돌아올 것 2) 모든 나라를 방문하되 동일 나라는 한 번만 방문할 것. 이번에도 역시 예를 들어 생각해 보자.
[예] 서울을 출발하여, 홍콩, 뉴욕, LA, 파리, 런던, 두바이를 방문하고 다시 서울로 돌아오는 여행을 계획 중이다. 이용할 수 있는 항공 노선표를 고려했을 때 어떤 경로로 여행을 해야 가장 효율적일까?

위의 모든 노선을 그래프로 그리면 다음과 같다. 이 그래프에서 서울을 출발하여 다시 서울로 돌아오는 최단 경로를 찾아보자. 출발점과 종착점이 같은 경우이므로 앞서 언급한 해밀턴 순환로를 찾으면 된다.
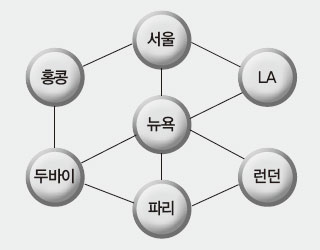
해밀턴 순환로를 찾을 때 반드시 지나야 하는 경로를 먼저 찾으면 훨씬 수월하게 경로를 찾을 수 있다. 이 그래프에서는 홍콩, 런던, LA가 연결된 노선이 2개밖에 없으므로 이 노선들은 입국과 출국으로 모두 이용해야 하는 노선들이다. 따라서 서울-홍콩, 홍콩-두바이, 서울-LA, LA-뉴욕, 뉴욕-런던, 런던-파리 노선은 반드시 이용해야 한다. 그럼 결국 ‘서울-홍콩-두바이-파리-런던-뉴욕-LA-서울’로 순환하는 한 가지 경로(방향만 반대인 경우는 같은 경로로 여긴다)밖에 없다. 즉 이 경로가 해밀턴 순환로가 된다. 이 경로를 따라 여행을 계획한다면, 적어도 갔던 경로를 다시 가게 되는 비효율적인 일정은 피할 수 있게 된다.
해밀턴 순환로가 여러 개라면? - 가중치 그래프
해밀턴 순환로만 찾는다고 해서 가장 효율적인 경로를 찾을 수 있을까? 아니다. 예시로 든 세계일주 경로는 해밀턴 순환로가 하나만 존재하기 때문에 효율적인 경로라고 할 수 있겠지만, LA-런던 노선이 새로 추가된 경우로 다시 살펴보자.
위의 그래프에 LA와 런던 사이에 선을 추가로 긋고 해밀턴 순환로를 다시 찾아보자.
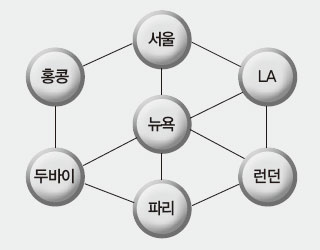
위에서 살펴봤듯이 서울-홍콩-두바이까지는 반드시 이용해야 하는 단일 경로지만, 두바이 다음의 경로가 뉴욕으로 가는 경우와 파리로 가는 경우로 나뉜다.
1) 뉴욕으로 가는 경우는 반드시 파리를 거쳐 런던으로 가야 하므로 서울-홍콩-두바이-뉴욕-파리-런던-LA-서울 경로가 해밀턴 순환로가 된다.
2) 두바이에서 파리로 가는 경우는 파리 이후 다음 세 가지 경로가 가능하다.
파리-뉴욕-런던-LA-서울, 파리-런던-뉴욕-LA-서울, 파리-런던-LA-뉴욕-서울
따라서 이 그래프에서 가능한 해밀턴 순환로는 다음 네 가지이다.
경로① 서울-홍콩-두바이-뉴욕-파리-런던-LA-서울
경로② 서울-홍콩-두바이-파리-뉴욕-런던-LA-서울
경로③ 서울-홍콩-두바이-파리-런던-뉴욕-LA-서울
경로④ 서울-홍콩-두바이-파리-런던-LA-뉴욕-서울
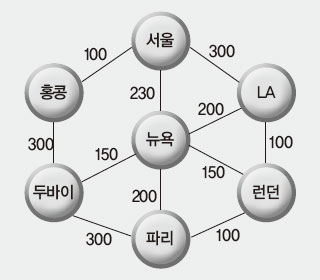
그렇다면 이 여러 개의 해밀턴 순환로 중 가장 효율적인 경로는 무엇일까? 우리가 효율성을 따질 때 고려하는 요소는 크게 시간, 거리, 돈 등이 있다. 여기서 거리와 이동 시간은 거의 동일하기 때문에 항공 노선에 따른 항공료를 함께 생각해서 최저비용으로 여행하는 경로를 찾아야 한다. 그래프 위에 노선별 항공료를 적어 네 가지 경우의 비용을 구해보면 다음과 같다.
경로① 1250, 경로② 1450, 경로③ 1450, 경로④ 1330
따라서 경로①로 여행계획을 짜는 것이 가장 효율적인 계획이 된다. 위와 같이 그래프 위에 같은 기준으로 환산한 중요도를 숫자로 적어놓은 그래프를 ‘가중치 그래프’라고 하는데 이는 최단 경로 알고리즘의 바탕이 된다.
빠른 길 찾기 - 최단 경로 알고리즘
우리가 빈번하게 사용하고 있는 빠른 길 찾기 애플리케이션의 원리가 바로 최단 경로 알고리즘이다. 최단 경로 알고리즘은 그래프상의 두 정점 사이를 연결하는 경로 중 가장 짧은 경로를 찾는 것을 말한다.
여기서 ‘짧다’는 것은 물리적인 거리 외에도 시간, 거리 혹은 비용, 거리 등 다양한 기준이 적용될 수 있다. 앞서 세계일주 경로를 찾을 때 사용했던 가중치 그래프에서는 거리의 기준을 비용, 거리로 나타냈었다. 이렇게 가중치 그래프로 나타낸 그래프 중 선 위의 값의 합이 최소 또는 최대가 되는 경로를 ‘최적의 경로’ 혹은 ‘최단 경로’라고 말한다. 사실 최적 경로를 찾는 알고리즘은 어떤 거리를 기준으로 가중치 그래프를 그릴 것이며, 또한 어떤 방법으로 최단 경로를 구해나갈 것인지에 따라 여러 가지 접근 방법이 있다.
앞서 우리가 살펴봤던 세계일주의 경우에는 네 가지의 경로를 모두 따져 값을 비교하는 방법을 택했지만, 우리가 사용하는 빠른 길 찾기 앱만 하더라도 해밀턴 순환로가 셀 수 없을 만큼 많을 것이며, 그때마다 모든 경로를 찾아 최단 거리를 계산하여 비교하며 구할 수는 없다. 따라서 최적 경로를 결정하는 효과적인 알고리즘을 찾기 위한 연구가 계속 진행 중인데, 가장 대표적인 최단 경로 알고리즘은 데이크스트라(Dijkstra) 알고리즘이다. 간단히 설명하면, 하나의 출발점에서 다른 모든 지점까지의 최단 경로를 구하는 방법이다. 데이크스트라 알고리즘의 과정은 다음과 같다.
① 가중치 그래프를 최단 거리를 나타내는 그래프로 만든다.
② 하나의 출발점을 정하여 직접 이어진 점까지의 최단 거리를 표에 정리하고, 그렇지 않은 점들은 빈 칸으로 놓아둔다. 여기서 빈 칸의 값은 무한대를 뜻한다.
③ 출발점과 거리가 가장 짧은 점부터 경로를 선택하여 다음 점까지의 거리를 또 구한다. 이때 지나간 경로는 색으로 칠한다.
④ 새로운 경로를 선택하면 그 점과 이어진 점까지의 거리를 구하고 이전에 이미 구한 거리와 비교해 작은 것을 택한다.
⑤ 그래프의 모든 경로가 색칠될 때까지 ③, ④의 과정을 반복한다.
이 방법이 우리가 사용하는 빠른 길 찾기 앱, 지하철 노선도 앱에 활용되는 알고리즘이다. 또한 도시계획을 할 때 지하철역의 위치와 백화점 위치 등을 정할 때도 이러한 그래프 알고리즘을 이용하여 가장 효율적인 지점을 찾곤 한다.
분명 동일한 시간 조건과 비용 조건 안에서 최적 계획법을 활용하여 조금 더 빨리 일을 끝내고, 가중치 그래프를 그려 최단 경로를 찾아 조금 더 빠른 길로 가는 것은 효율적이다. 그러나 항상 효율적인 것이 좋은 것일까? 라는 의문이 든다.
효율적인 삶도 중요하지만 너무 바쁘게만 달려가는 현대사회에서 때론 자연과 더불어 조금 더 여유롭게 지내는 것도 필요할 것이다.⊙
효율적 생산을 위해서 - 최적 계획법
약 2년 전 한 감자칩이 품귀현상을 불러일으키며 폭발적인 인기를 누렸다. 시중에서 구하기가 매우 어려웠는데 ‘제조업체가 일부러 생산량을 조절하는 것이 아닌가’ 하는 소문까지 돌았다. 실제로 감자칩 제조 회사는 공장을 24시간 풀가동했을 뿐만 아니라 분명 가장 효율적인 방법으로 감자칩을 만들었을 것이다.
여기서 효율적인 방법이란 무엇일까? 하루 24시간 안에 보다 더 많은 과자를 만들어 내는 방법이 효율적인 방법일 것이다. 이처럼 짧은 시간 등과 같이 주어진 제약 조건하에서 효율을 극대화할 수 있게 하는 계획법을 ‘최적 계획법’이라고 한다.
다음 예를 보면서 최적 계획법에 대해 알아보자.
[예] 이해하기 쉽게 감자칩 한 봉지를 만드는 방법을 예로 살펴보자.

작업 방법을 참고하여 감자칩을 만들 때, A부터 F까지 순서대로 한다면 과자를 만드는 데 걸리는 시간은 총 3+2+3+5+7+10=30분이 걸린다. 이보다 짧은 시간에 감자칩을 만들 수는 없을까? 최적 계획을 세우기 위해서는 많은 것을 고려해야 하지만 가장 중요하게 고려되는 조건은 바로 시간이다. 그렇다면 시간을 단축하기 위해서는 어떻게 해야 할까? 우선, 반드시 순서를 지켜야 하는 일을 정리한다. 그런 후에 동시에 할 수 있는 일들을 찾는다. 이를 기억한 채로 다시 감자칩 만드는 작업으로 돌아가 보자.
A~F의 작업 중 일의 순서에 따라 그림으로 나타내면 다음과 같다.

그림 ( )의 숫자는 걸리는 시간을 의미한다.
즉 작업 C, D, F는 동시에 해도 된다. 따라서 작업하는 데 걸리는 최소 시간은 동시에 해도 되는 작업 중 가장 많은 시간을 소요하는 작업을 지나는 경로의 시간을 합하면 되므로 3+2+7+10=22분이 된다.
우리는 사실 위와 같은 최적 계획법을 빈번하게 사용하고 있다. 매일 저녁 아내가 최대한 빨리 따끈하고 맛있는 저녁상을 차려낼 때도 최적 계획법이 사용될 수 있으며, 업무를 할 때도 알게 모르게 최적 계획법에 맞게 효율적인 업무를 하고 있을 것이다.
총알배송을 위한 경로 - 해밀턴 순환로
‘주문이 완료되었습니다. 주문하신 상품은 내일 바로 받아보실 수 있습니다.’
평일의 경우 밤 10시 전에 주문한 상품은 다음날 바로 받아볼 수 있다. 배송의 속도 경쟁이 치열한 요즘 총알배송, 로켓배송, 스마트배송 등 이른바 빠른 배송 시스템은 온라인 상품 판매 업체들에 빠져서는 안 될 마케팅 서비스 중 하나로 자리 잡았다. 적은 인력으로 최대한 빨리 배송을 하기 위해서 갔던 길을 다시 돌지 않는 최적 경로를 찾아 배송을 해야 한다. 다음의 경우를 생각해 보자.

[예] 택배회사를 출발하여 A, B, C 세 곳을 모두 들러 상품을 배달하고 다시 택배회사로 돌아올 때 가장 효율적인 경로는 어떤 경로인지 생각해 보자. [택배회사 → B → A → C → 택배회사] 이 경로가 왔던 길을 다시 되돌아가지 않는 가장 효율적인 경로가 될 것이다. 단순한 예를 살펴봤지만 이는 그래프 이론 중 최적화 이론의 대표적인 예이다. 이러한 경로를 ‘해밀턴 경로’라고 하는데, 연결된 그래프로 나타낸 경로 중 모든 꼭짓점을 오직 한 번씩만 지나는 경로를 말한다. 해밀턴 경로 중에 출발점과 종착점이 같은 경우는 ‘해밀턴 순환로’라고 한다. 이 해밀턴 경로 이론을 적용할 수 있는 적절한 상황은 세계여행 경로를 계획할 때이다.
효율적인 세계일주 경로
세계일주 하는 사람들은 대개 저렴한 비용으로 가장 효율적으로 이동할 수 있는 경로를 찾아 여행 계획을 세운다. 이때 반드시 지켜야 하는 조건은 아래 두 가지이다.
1) 서울을 출발하여 서울로 다시 돌아올 것 2) 모든 나라를 방문하되 동일 나라는 한 번만 방문할 것. 이번에도 역시 예를 들어 생각해 보자.
[예] 서울을 출발하여, 홍콩, 뉴욕, LA, 파리, 런던, 두바이를 방문하고 다시 서울로 돌아오는 여행을 계획 중이다. 이용할 수 있는 항공 노선표를 고려했을 때 어떤 경로로 여행을 해야 가장 효율적일까?

위의 모든 노선을 그래프로 그리면 다음과 같다. 이 그래프에서 서울을 출발하여 다시 서울로 돌아오는 최단 경로를 찾아보자. 출발점과 종착점이 같은 경우이므로 앞서 언급한 해밀턴 순환로를 찾으면 된다.

해밀턴 순환로를 찾을 때 반드시 지나야 하는 경로를 먼저 찾으면 훨씬 수월하게 경로를 찾을 수 있다. 이 그래프에서는 홍콩, 런던, LA가 연결된 노선이 2개밖에 없으므로 이 노선들은 입국과 출국으로 모두 이용해야 하는 노선들이다. 따라서 서울-홍콩, 홍콩-두바이, 서울-LA, LA-뉴욕, 뉴욕-런던, 런던-파리 노선은 반드시 이용해야 한다. 그럼 결국 ‘서울-홍콩-두바이-파리-런던-뉴욕-LA-서울’로 순환하는 한 가지 경로(방향만 반대인 경우는 같은 경로로 여긴다)밖에 없다. 즉 이 경로가 해밀턴 순환로가 된다. 이 경로를 따라 여행을 계획한다면, 적어도 갔던 경로를 다시 가게 되는 비효율적인 일정은 피할 수 있게 된다.
해밀턴 순환로가 여러 개라면? - 가중치 그래프
해밀턴 순환로만 찾는다고 해서 가장 효율적인 경로를 찾을 수 있을까? 아니다. 예시로 든 세계일주 경로는 해밀턴 순환로가 하나만 존재하기 때문에 효율적인 경로라고 할 수 있겠지만, LA-런던 노선이 새로 추가된 경우로 다시 살펴보자.
위의 그래프에 LA와 런던 사이에 선을 추가로 긋고 해밀턴 순환로를 다시 찾아보자.

위에서 살펴봤듯이 서울-홍콩-두바이까지는 반드시 이용해야 하는 단일 경로지만, 두바이 다음의 경로가 뉴욕으로 가는 경우와 파리로 가는 경우로 나뉜다.
1) 뉴욕으로 가는 경우는 반드시 파리를 거쳐 런던으로 가야 하므로 서울-홍콩-두바이-뉴욕-파리-런던-LA-서울 경로가 해밀턴 순환로가 된다.
2) 두바이에서 파리로 가는 경우는 파리 이후 다음 세 가지 경로가 가능하다.
파리-뉴욕-런던-LA-서울, 파리-런던-뉴욕-LA-서울, 파리-런던-LA-뉴욕-서울
따라서 이 그래프에서 가능한 해밀턴 순환로는 다음 네 가지이다.
경로① 서울-홍콩-두바이-뉴욕-파리-런던-LA-서울
경로② 서울-홍콩-두바이-파리-뉴욕-런던-LA-서울
경로③ 서울-홍콩-두바이-파리-런던-뉴욕-LA-서울
경로④ 서울-홍콩-두바이-파리-런던-LA-뉴욕-서울

그렇다면 이 여러 개의 해밀턴 순환로 중 가장 효율적인 경로는 무엇일까? 우리가 효율성을 따질 때 고려하는 요소는 크게 시간, 거리, 돈 등이 있다. 여기서 거리와 이동 시간은 거의 동일하기 때문에 항공 노선에 따른 항공료를 함께 생각해서 최저비용으로 여행하는 경로를 찾아야 한다. 그래프 위에 노선별 항공료를 적어 네 가지 경우의 비용을 구해보면 다음과 같다.
경로① 1250, 경로② 1450, 경로③ 1450, 경로④ 1330
따라서 경로①로 여행계획을 짜는 것이 가장 효율적인 계획이 된다. 위와 같이 그래프 위에 같은 기준으로 환산한 중요도를 숫자로 적어놓은 그래프를 ‘가중치 그래프’라고 하는데 이는 최단 경로 알고리즘의 바탕이 된다.
빠른 길 찾기 - 최단 경로 알고리즘
우리가 빈번하게 사용하고 있는 빠른 길 찾기 애플리케이션의 원리가 바로 최단 경로 알고리즘이다. 최단 경로 알고리즘은 그래프상의 두 정점 사이를 연결하는 경로 중 가장 짧은 경로를 찾는 것을 말한다.
여기서 ‘짧다’는 것은 물리적인 거리 외에도 시간, 거리 혹은 비용, 거리 등 다양한 기준이 적용될 수 있다. 앞서 세계일주 경로를 찾을 때 사용했던 가중치 그래프에서는 거리의 기준을 비용, 거리로 나타냈었다. 이렇게 가중치 그래프로 나타낸 그래프 중 선 위의 값의 합이 최소 또는 최대가 되는 경로를 ‘최적의 경로’ 혹은 ‘최단 경로’라고 말한다. 사실 최적 경로를 찾는 알고리즘은 어떤 거리를 기준으로 가중치 그래프를 그릴 것이며, 또한 어떤 방법으로 최단 경로를 구해나갈 것인지에 따라 여러 가지 접근 방법이 있다.
앞서 우리가 살펴봤던 세계일주의 경우에는 네 가지의 경로를 모두 따져 값을 비교하는 방법을 택했지만, 우리가 사용하는 빠른 길 찾기 앱만 하더라도 해밀턴 순환로가 셀 수 없을 만큼 많을 것이며, 그때마다 모든 경로를 찾아 최단 거리를 계산하여 비교하며 구할 수는 없다. 따라서 최적 경로를 결정하는 효과적인 알고리즘을 찾기 위한 연구가 계속 진행 중인데, 가장 대표적인 최단 경로 알고리즘은 데이크스트라(Dijkstra) 알고리즘이다. 간단히 설명하면, 하나의 출발점에서 다른 모든 지점까지의 최단 경로를 구하는 방법이다. 데이크스트라 알고리즘의 과정은 다음과 같다.
① 가중치 그래프를 최단 거리를 나타내는 그래프로 만든다.
② 하나의 출발점을 정하여 직접 이어진 점까지의 최단 거리를 표에 정리하고, 그렇지 않은 점들은 빈 칸으로 놓아둔다. 여기서 빈 칸의 값은 무한대를 뜻한다.
③ 출발점과 거리가 가장 짧은 점부터 경로를 선택하여 다음 점까지의 거리를 또 구한다. 이때 지나간 경로는 색으로 칠한다.
④ 새로운 경로를 선택하면 그 점과 이어진 점까지의 거리를 구하고 이전에 이미 구한 거리와 비교해 작은 것을 택한다.
⑤ 그래프의 모든 경로가 색칠될 때까지 ③, ④의 과정을 반복한다.
이 방법이 우리가 사용하는 빠른 길 찾기 앱, 지하철 노선도 앱에 활용되는 알고리즘이다. 또한 도시계획을 할 때 지하철역의 위치와 백화점 위치 등을 정할 때도 이러한 그래프 알고리즘을 이용하여 가장 효율적인 지점을 찾곤 한다.
분명 동일한 시간 조건과 비용 조건 안에서 최적 계획법을 활용하여 조금 더 빨리 일을 끝내고, 가중치 그래프를 그려 최단 경로를 찾아 조금 더 빠른 길로 가는 것은 효율적이다. 그러나 항상 효율적인 것이 좋은 것일까? 라는 의문이 든다.
효율적인 삶도 중요하지만 너무 바쁘게만 달려가는 현대사회에서 때론 자연과 더불어 조금 더 여유롭게 지내는 것도 필요할 것이다.⊙
월간조선.
댓글 없음:
댓글 쓰기