⊙ 매듭, 화학의 분자식 등에도 수학적 원리 작용
 |
한 잔의 커피와 도넛, 바쁜 현대인들을 위한 간편한 식사가 될 수도 있지만 수학자에게는 이 또한 수학적 대상인 수학적 객체로 보이기도 한다. 수학의 많은 분야 중 하나인 위상수학에서는 머그컵과 도넛을 같다고 말한다.
어린 시절을 떠올려보면 ‘삼각형과 사각형은 서로 다른 것이다’ ‘변의 길이가 다른 도형은 합동이 아니다’ 등으로 완전히 같지 않으면 다른 것으로 취급하는 ‘엄밀한’ 수학에서 대뜸 머그컵과 도넛이 같다고 하니 약간 어이가 없지 않은가?
이는 수학이 ‘엄밀하기’ 때문에 생기는 것으로, 어느 관점에서 ‘같다’는 것인지를 확실히 하고 가야 한다. 삼각형과 사각형은 내각의 합이 180도, 360도로 서로 다르고, 변의 개수도 3개와 4개로 같은 부분이 없어 보인다. 하지만 삼각형이 만약 고무점토로 만들어져 있다면 고무점토를 따로 자르거나 찢거나 공간을 하나로 합치지 않고 잘 구부리기만 해서 사각형으로 쉽게 모양을 바꿀 수 있을 것이다. 위상수학에서는 이처럼 머그컵과 도넛을 고무점토로 보고 고무점토를 구부려 서로를 만들 수 있기에 같다고 말한다.
고리로 보는 도형

고무점토라고 생각하면 도넛으로 무엇이든 만들 수 있을 것 같고 어떤 모양이든 다 같은 것 아닌가 하는 생각이 든다. 그렇다면 두 도형이 다르다고 할 때, 고무점토를 아무리 구부려도 같은 모양을 만들 수 없기에 다르다고 해야 할까?
수학자들은 두 도형이 위상적으로 같지 않다는 것을 증명하기 위해 이번에는 잘 늘어나고 줄어드는 ‘고리’(양 끝이 붙어 있는 끈)를 이용한다. 도넛을 잘 구부려서 머그컵을 만들 수는 있지만 지구와 같은 구 모양은 만들 수가 없는데, 도넛과 머그컵 손잡이에 있는 구멍이 그 이유이다.
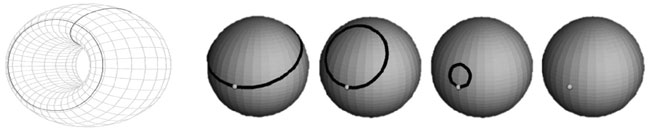
고무점토를 잘 구부린다고 해도 구멍이 사라지진 않기 때문인데, 고리를 통해 구멍의 존재 유무와 개수를 알아낼 수 있다. 그림과 같이 고리가 도넛에 둘러져 있으면, 고리를 아무리 늘리거나 줄이면서 이동시켜도(단, 도넛의 표면 위에서 고리를 움직여야 한다) 한 점에 오게 만들 수가 없지만 동그란 구에서는 고리를 점차 축소시키면 한 점에 모이게 할 수 있다.
이렇게 도형에 고리를 둘러보고 축소시켜 보면서 수학자들은 도형에 구멍이 있는지를 판단하고 위상학적으로 다른 도형이라고 말한다. 또한 도넛 그림의 두 고리는 서로 한 점에서 교차하지만 아무리 움직여도 같은 위치에 있을 수는 없는데, 이를 통해 같은 도형에서도 서로 다른 고리가 존재하는 것을 알 수 있고 이런 고리들이 얼마나 존재하는지를 통해 구멍의 개수를 파악한다.
우리는 오늘날 인공위성을 통해 지구의 모습을 보며 지구는 둥글다는 것을 알고 있다. 그리고 배를 타고 지구를 한 바퀴 돈 마젤란을 통해 실험적으로도 둥근 것이 증명되었다고 생각한다.
하지만 이제 마젤란은 지구라는 도형에 고리(마젤란이 항해한 경로)를 만들었을 뿐, 그 고리를 충분히 당겨 구멍이 없다는 것을 보이지 않음을 알 수 있을 것이다. 사실 지구 한 바퀴를 도는 것은 지구가 도넛 모양이어도 가능하지 않은가.
앙리 푸앵카레 고리와 우주의 모양
마젤란의 세계 일주가 지구가 둥글다는 것에 대한 증명이 되지는 못하지만, 굉장히 의미 있는 행동임은 분명하며 인류 역사적으로 높이 평가받고 있다. 그렇다면 이토록 의미 있는 행동을 우주에서 해보면 어떨까? 우주에서 무한한 길이의 끈을 맨 로켓을 타고 마젤란처럼 일주하다 지구로 다시 돌아온다고 생각해 보자.
어떻게 여행을 하더라도 로켓에 매단 끈을 당겨 회수할 수 있다면, 우리는 마젤란이 그랬던 것처럼 우주가 둥글다고 말할 수 있을까? 이 질문은 19세기 말에서 20세기 초에 활동한 저명한 수학자 앙리 푸앵카레(Jules-Henri Poincaré)가 한 추측이다.
“단일 연결인 3차원에 닫힌 다양체는 3차원 구와 위상동형이다”라는 추측으로, 100년 가까이 풀리지 않고 2000년에 와서는 밀레니엄 문제로 선정되어 100만 달러의 상금이 붙은 문제가 되었다. 이 추측은 100년에 걸쳐 난제로 남았는데, 미국의 수학자 윌리엄 서스턴(William Paul Thurston)은 우주의 전체 모양을 생각하기 이전에 기본적인 모양부터 생각함으로써 이 문제에 대한 해결책을 찾으려고 했다.
우리는 지구에 살지만 2차원 평면으로 만든 지도를 사용하는데, 이는 우리가 사는 지구가 2차원 다양체이기 때문에 2차원 좌표를 이용해 위치를 나타내는 것이 가능하기 때문이다. 지구와 같은 2차원 다양체는 동그란 구와 도넛, 실사영평면이라는 3개의 조각을 여러 개 이어붙이면 만들 수 있다. 이는 다음과 같이 도넛 3개를 붙이면 프레첼 모양을 만들 수 있는 것과 같은 이야기이다.

그리고리 페렐만
서스턴은 이 작업을 3차원 다양체에 도입하였고 그 결과 우주가 어떤 모양이어도 8개의 조각을 여러 개 사용하면 만들 수 있다는 ‘기하화 추측’에 도달하게 되었다. 하지만 추측이라는 것에서 알 수 있듯이 이 또한 증명은 되지 않았지만, 푸앵카레의 추측을 푸는 가장 큰 실마리가 되었다.
그 후 2002년 러시아의 수학자 그리고리 페렐만에 의해 기하화 추측이 증명됨으로써, 푸앵카레의 추측은 참으로 증명되었다. 난제 해결로 일약 스타가 된 페렐만은 문제에 걸렸던 상금도 받지 않고 수학계의 노벨상이라 불리는 필즈상도 거부한 채 은둔하여 연구에 몰두하고 있다.
고리를 통해 우리는 도형이 위상적으로 같은지, 즉 구멍이 있는지 없는지를 판별할 수 있었다. 그리고 여기에 고리로 할 수 있는 또 하나의 수학이 있다. 우리는 끈을 여러 방향으로 꼬아서 물건을 단단히 고정하거나 외형을 꾸미는 등의 매듭을 만드는데, 수학에서는 매듭 이론(Knot Theory)이라는 이름으로 두 개의 매듭이 서로 같은지 다른지를 연구한다.
그렇다면 두 매듭이 같다는 것은 어떤 것을 기준으로 할까? 매듭 이론에서는 고리로 만든 매듭을 가위로 자르지 않고 변형시켜서 다른 매듭을 만들 수 있다면 같은 매듭이라고 한다. 매듭을 자르지 않고 움직이는 방법은 ‘라이데마이스터(Reidemeister) 변환’이라고 불리며 매듭에 꼬임을 만들거나 없애기, 엇갈림을 만들거나 없애기, 엇갈림의 한편에 있는 가닥을 엇갈림의 반대편으로 옮기기로 세 가지가 있다.
거창하게 수학자의 이름이 붙긴 했지만, 어릴 때 해본 실뜨기의 원리와 동일하다. 중요한 것은 매듭을 자르지 않고 움직이는 것이다. 그럼 다음의 두 매듭이 같은지 다른지 라이데마이스터 변환을 적용해 보길 바란다.
고리를 움직여 본 사람들은 눈치챘겠지만 위의 두 매듭은 라이데마이스터 변환으로는 서로 같아질 수 없는 다른 매듭이다.
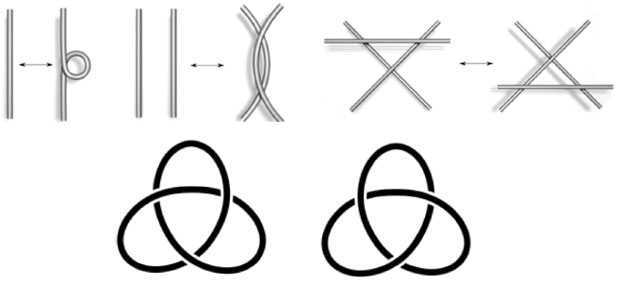
매듭과 DNA
얼핏 보면 서로 같아 보이는 이 두 매듭은 거울에 대칭된 모습으로, 이와 같은 것으로 1960년대에 전 세계적으로 비극적인 일이 일어나기도 했다. ‘탈리도마이드’라는 분자를 이용해 입덧 방지제를 만들었는데, 분자의 내부 구조가 모습은 같지만 거울대칭인 분자가 존재하였고 이 거울대칭인 탈리도마이드 분자로 만든 입덧 방지제는 세계적으로 1만2000여 명의 기형아를 낳는 원인이 되었던 것이다. 이처럼 서로 같은 분자식을 가지는 분자도 매듭 구조에 따라 다른 작용을 하기도 한다.
매듭에 관련된 연구는 수학적 연구 이전부터 화학자들에 의해서 연구되기 시작했는데, 수리물리학자 캘빈(William Thomson Kelvin)이 물질을 구성하는 원자가 에테르라 불리는 물질이 가지는 매듭이라고 한 가설이 그 시작이다.
물리학자 피터 거스리 테이트(Peter Guthrie Tait)는 이 가설에 따라 가능한 모든 매듭을 나열하며 원소표를 만들기도 했는데, 캘빈의 가설이 틀렸다는 사실이 밝혀지고 원자모형에 대한 새로운 분석이 이루어지자 매듭에 대한 의미 역시 사라져갔다.
하지만 20세기 후반 DNA의 분자구조에서 매듭 현상이 발생하는 것을 발견하게 되면서 수학자들이 이루어놓은 매듭 이론이 다시금 빛을 보게 된다. 생명체의 유전정보를 담고 있는 DNA는 이중나선 구조로 되어 있으며, 이중나선 자체적으로도 비틀려 있어 마치 전화기의 선과 같은 모양으로 초꼬임(supercoiling)의 형태를 가진다.
DNA에 작용하는 특정 효소들을 이용하면 나선구조의 중간부분을 끊고 비틀림을 풀어 재조합이 가능한데, 이를 이용하여 바이러스에 감염되어 매듭을 짓고 있는 DNA를 분석하거나 매듭을 더해 기존에 알려지지 않은 물질을 얻는 등으로 DNA 연구에 매듭이 사용된다.
수학자와 수학적 대상
수학자들은 어떠한 대상을 분석할 때, 대상의 변하지 않는 것(불변량)에 주목하고 그 변하지 않는 것을 파악하는 방법에 초점을 맞춘다. 고무점토, 고리, 매듭 등은 수학적 대상으로 보이지 않지만, 모두 이런 관점에서 생긴 수학적 대상이다.
수가 아닌 다양한 도구로 설명된 위상수학은 그 표면을 보면 놀잇감 정도로 생각될 수도 있지만, 내부는 다른 수학과 마찬가지로 논리로 가득 차 있으며 그 응용은 놀라운 과학의 발견으로 이어진다. 위상수학에서 나온 정리 중 재미있는 결과를 나타내는 정리로 마무리를 하려 한다.
위상수학의 경우 ‘지구상의 두 대척점 중 어딘가는 서로 같은 온도와 같은 바람 속도를 가진다’와 ‘지구 어딘가에는 바람이 불지 않는 곳이 적어도 한 곳은 있다’가 참인 명제라고 말한다.
오일러의 베타 함수가 200년이 지나 물리학 초끈이론의 시작이 되었듯이, 수학자들이 연구하는 것이 비단 수와 같은 수학적 대상에 국한되는 것이 아니라 현재 혹은 미래 과학 전반에 대한 연구임을 느낄 수 있을 것이다.⊙
어린 시절을 떠올려보면 ‘삼각형과 사각형은 서로 다른 것이다’ ‘변의 길이가 다른 도형은 합동이 아니다’ 등으로 완전히 같지 않으면 다른 것으로 취급하는 ‘엄밀한’ 수학에서 대뜸 머그컵과 도넛이 같다고 하니 약간 어이가 없지 않은가?
이는 수학이 ‘엄밀하기’ 때문에 생기는 것으로, 어느 관점에서 ‘같다’는 것인지를 확실히 하고 가야 한다. 삼각형과 사각형은 내각의 합이 180도, 360도로 서로 다르고, 변의 개수도 3개와 4개로 같은 부분이 없어 보인다. 하지만 삼각형이 만약 고무점토로 만들어져 있다면 고무점토를 따로 자르거나 찢거나 공간을 하나로 합치지 않고 잘 구부리기만 해서 사각형으로 쉽게 모양을 바꿀 수 있을 것이다. 위상수학에서는 이처럼 머그컵과 도넛을 고무점토로 보고 고무점토를 구부려 서로를 만들 수 있기에 같다고 말한다.
고리로 보는 도형

고무점토라고 생각하면 도넛으로 무엇이든 만들 수 있을 것 같고 어떤 모양이든 다 같은 것 아닌가 하는 생각이 든다. 그렇다면 두 도형이 다르다고 할 때, 고무점토를 아무리 구부려도 같은 모양을 만들 수 없기에 다르다고 해야 할까?
수학자들은 두 도형이 위상적으로 같지 않다는 것을 증명하기 위해 이번에는 잘 늘어나고 줄어드는 ‘고리’(양 끝이 붙어 있는 끈)를 이용한다. 도넛을 잘 구부려서 머그컵을 만들 수는 있지만 지구와 같은 구 모양은 만들 수가 없는데, 도넛과 머그컵 손잡이에 있는 구멍이 그 이유이다.
고무점토를 잘 구부린다고 해도 구멍이 사라지진 않기 때문인데, 고리를 통해 구멍의 존재 유무와 개수를 알아낼 수 있다. 그림과 같이 고리가 도넛에 둘러져 있으면, 고리를 아무리 늘리거나 줄이면서 이동시켜도(단, 도넛의 표면 위에서 고리를 움직여야 한다) 한 점에 오게 만들 수가 없지만 동그란 구에서는 고리를 점차 축소시키면 한 점에 모이게 할 수 있다.
이렇게 도형에 고리를 둘러보고 축소시켜 보면서 수학자들은 도형에 구멍이 있는지를 판단하고 위상학적으로 다른 도형이라고 말한다. 또한 도넛 그림의 두 고리는 서로 한 점에서 교차하지만 아무리 움직여도 같은 위치에 있을 수는 없는데, 이를 통해 같은 도형에서도 서로 다른 고리가 존재하는 것을 알 수 있고 이런 고리들이 얼마나 존재하는지를 통해 구멍의 개수를 파악한다.
우리는 오늘날 인공위성을 통해 지구의 모습을 보며 지구는 둥글다는 것을 알고 있다. 그리고 배를 타고 지구를 한 바퀴 돈 마젤란을 통해 실험적으로도 둥근 것이 증명되었다고 생각한다.
하지만 이제 마젤란은 지구라는 도형에 고리(마젤란이 항해한 경로)를 만들었을 뿐, 그 고리를 충분히 당겨 구멍이 없다는 것을 보이지 않음을 알 수 있을 것이다. 사실 지구 한 바퀴를 도는 것은 지구가 도넛 모양이어도 가능하지 않은가.
앙리 푸앵카레 고리와 우주의 모양

마젤란의 세계 일주가 지구가 둥글다는 것에 대한 증명이 되지는 못하지만, 굉장히 의미 있는 행동임은 분명하며 인류 역사적으로 높이 평가받고 있다. 그렇다면 이토록 의미 있는 행동을 우주에서 해보면 어떨까? 우주에서 무한한 길이의 끈을 맨 로켓을 타고 마젤란처럼 일주하다 지구로 다시 돌아온다고 생각해 보자.
 |
| 앙리 푸앵카레. |
“단일 연결인 3차원에 닫힌 다양체는 3차원 구와 위상동형이다”라는 추측으로, 100년 가까이 풀리지 않고 2000년에 와서는 밀레니엄 문제로 선정되어 100만 달러의 상금이 붙은 문제가 되었다. 이 추측은 100년에 걸쳐 난제로 남았는데, 미국의 수학자 윌리엄 서스턴(William Paul Thurston)은 우주의 전체 모양을 생각하기 이전에 기본적인 모양부터 생각함으로써 이 문제에 대한 해결책을 찾으려고 했다.
우리는 지구에 살지만 2차원 평면으로 만든 지도를 사용하는데, 이는 우리가 사는 지구가 2차원 다양체이기 때문에 2차원 좌표를 이용해 위치를 나타내는 것이 가능하기 때문이다. 지구와 같은 2차원 다양체는 동그란 구와 도넛, 실사영평면이라는 3개의 조각을 여러 개 이어붙이면 만들 수 있다. 이는 다음과 같이 도넛 3개를 붙이면 프레첼 모양을 만들 수 있는 것과 같은 이야기이다.

그리고리 페렐만
 |
| 그리고리 페렐만. |
그 후 2002년 러시아의 수학자 그리고리 페렐만에 의해 기하화 추측이 증명됨으로써, 푸앵카레의 추측은 참으로 증명되었다. 난제 해결로 일약 스타가 된 페렐만은 문제에 걸렸던 상금도 받지 않고 수학계의 노벨상이라 불리는 필즈상도 거부한 채 은둔하여 연구에 몰두하고 있다.
고리를 통해 우리는 도형이 위상적으로 같은지, 즉 구멍이 있는지 없는지를 판별할 수 있었다. 그리고 여기에 고리로 할 수 있는 또 하나의 수학이 있다. 우리는 끈을 여러 방향으로 꼬아서 물건을 단단히 고정하거나 외형을 꾸미는 등의 매듭을 만드는데, 수학에서는 매듭 이론(Knot Theory)이라는 이름으로 두 개의 매듭이 서로 같은지 다른지를 연구한다.
그렇다면 두 매듭이 같다는 것은 어떤 것을 기준으로 할까? 매듭 이론에서는 고리로 만든 매듭을 가위로 자르지 않고 변형시켜서 다른 매듭을 만들 수 있다면 같은 매듭이라고 한다. 매듭을 자르지 않고 움직이는 방법은 ‘라이데마이스터(Reidemeister) 변환’이라고 불리며 매듭에 꼬임을 만들거나 없애기, 엇갈림을 만들거나 없애기, 엇갈림의 한편에 있는 가닥을 엇갈림의 반대편으로 옮기기로 세 가지가 있다.
거창하게 수학자의 이름이 붙긴 했지만, 어릴 때 해본 실뜨기의 원리와 동일하다. 중요한 것은 매듭을 자르지 않고 움직이는 것이다. 그럼 다음의 두 매듭이 같은지 다른지 라이데마이스터 변환을 적용해 보길 바란다.
고리를 움직여 본 사람들은 눈치챘겠지만 위의 두 매듭은 라이데마이스터 변환으로는 서로 같아질 수 없는 다른 매듭이다.
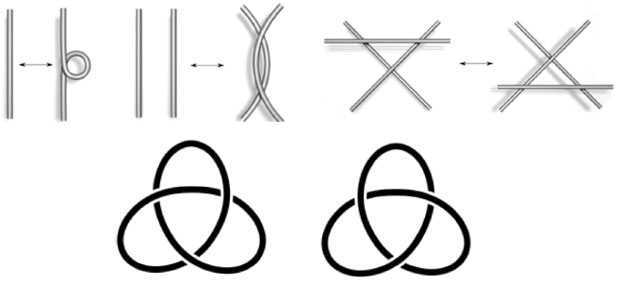
매듭과 DNA
얼핏 보면 서로 같아 보이는 이 두 매듭은 거울에 대칭된 모습으로, 이와 같은 것으로 1960년대에 전 세계적으로 비극적인 일이 일어나기도 했다. ‘탈리도마이드’라는 분자를 이용해 입덧 방지제를 만들었는데, 분자의 내부 구조가 모습은 같지만 거울대칭인 분자가 존재하였고 이 거울대칭인 탈리도마이드 분자로 만든 입덧 방지제는 세계적으로 1만2000여 명의 기형아를 낳는 원인이 되었던 것이다. 이처럼 서로 같은 분자식을 가지는 분자도 매듭 구조에 따라 다른 작용을 하기도 한다.
매듭에 관련된 연구는 수학적 연구 이전부터 화학자들에 의해서 연구되기 시작했는데, 수리물리학자 캘빈(William Thomson Kelvin)이 물질을 구성하는 원자가 에테르라 불리는 물질이 가지는 매듭이라고 한 가설이 그 시작이다.
물리학자 피터 거스리 테이트(Peter Guthrie Tait)는 이 가설에 따라 가능한 모든 매듭을 나열하며 원소표를 만들기도 했는데, 캘빈의 가설이 틀렸다는 사실이 밝혀지고 원자모형에 대한 새로운 분석이 이루어지자 매듭에 대한 의미 역시 사라져갔다.
하지만 20세기 후반 DNA의 분자구조에서 매듭 현상이 발생하는 것을 발견하게 되면서 수학자들이 이루어놓은 매듭 이론이 다시금 빛을 보게 된다. 생명체의 유전정보를 담고 있는 DNA는 이중나선 구조로 되어 있으며, 이중나선 자체적으로도 비틀려 있어 마치 전화기의 선과 같은 모양으로 초꼬임(supercoiling)의 형태를 가진다.
DNA에 작용하는 특정 효소들을 이용하면 나선구조의 중간부분을 끊고 비틀림을 풀어 재조합이 가능한데, 이를 이용하여 바이러스에 감염되어 매듭을 짓고 있는 DNA를 분석하거나 매듭을 더해 기존에 알려지지 않은 물질을 얻는 등으로 DNA 연구에 매듭이 사용된다.
수학자와 수학적 대상
수학자들은 어떠한 대상을 분석할 때, 대상의 변하지 않는 것(불변량)에 주목하고 그 변하지 않는 것을 파악하는 방법에 초점을 맞춘다. 고무점토, 고리, 매듭 등은 수학적 대상으로 보이지 않지만, 모두 이런 관점에서 생긴 수학적 대상이다.
수가 아닌 다양한 도구로 설명된 위상수학은 그 표면을 보면 놀잇감 정도로 생각될 수도 있지만, 내부는 다른 수학과 마찬가지로 논리로 가득 차 있으며 그 응용은 놀라운 과학의 발견으로 이어진다. 위상수학에서 나온 정리 중 재미있는 결과를 나타내는 정리로 마무리를 하려 한다.
위상수학의 경우 ‘지구상의 두 대척점 중 어딘가는 서로 같은 온도와 같은 바람 속도를 가진다’와 ‘지구 어딘가에는 바람이 불지 않는 곳이 적어도 한 곳은 있다’가 참인 명제라고 말한다.
오일러의 베타 함수가 200년이 지나 물리학 초끈이론의 시작이 되었듯이, 수학자들이 연구하는 것이 비단 수와 같은 수학적 대상에 국한되는 것이 아니라 현재 혹은 미래 과학 전반에 대한 연구임을 느낄 수 있을 것이다.⊙
월간조선
댓글 없음:
댓글 쓰기