⊙ 분할자와 선택자를 달리하는 분할선택법은 모두를 만족시킬 수 있어
⊙ 솔로몬의 선택은 일종의 ‘봉인된 입찰법’
 |
우리는 살아가면서 다른 사람과 물건을 서로 나누어 가지는 상황을 자주 접한다. 어린 시절 짝과 책상을 나누어 사용할 때, 서로 공평하게 쓰기 위해 책상 정중앙에 선을 그리기도 했다. 나눠 가지는 것으로 가장 많이 싸우는 것은 아무래도 먹는 것이 아닐까? 형제, 자매에게 먹을 것을 줄 때, 항상 똑같이 주지 않으면 울기도 하고 화내기도 한다. 사탕 같은 것은 개별포장이 되어 있어 하나씩 나누어 주기 좋은 편이지만, 빵 같은 경우는 잘라 주어야 하기에 똑같이 나누기가 힘들다. 만약 빵이 동그랗거나 일정한 모양이 아니라 위와 같은 모양으로 생겼다면 정확히 반을 자를 수 있을까?
예전에 잠시 언급했던 부분이지만 우리 생활에 있는 대부분의 것들은 ‘연속적’인 물체들로 위와 같은 모양의 빵도 마찬가지다. 빵이 연속적인 물체이기 때문에, 어느 한쪽부터 선을 그어 두 부분의 넓이를 비교해 보면 그 비율이 어느 순간 5대5가 되는 경우가 반드시 생기며 그때 빵을 잘라 두 사람에게 나누어 주면 된다. 그렇다면 두 개의 빵 사이에 햄이 끼워져 있는 ‘햄 샌드위치’는 빵과 햄을 모두 펼쳐 놓은 뒤, 각각 반으로 자르고 다시 합쳐야 할까?
폴란드의 유명한 수학자인 바나흐(Stefan Banach)에 의해 증명된 ‘햄 샌드위치 정리’는 ‘한 번의 칼질’로 햄 샌드위치를 정확히 반으로 자르는 것이 가능하다고 이야기한다. ‘햄 샌드위치 정리’는 일반적인 n차원에 대해서도 적용 가능한데, ‘n차원의 측정 가능한 물체 n개는 (n-1)차원의 평면 한 개로 각각의 물체를 정확히 이등분할 수 있다’는 게 그 내용이다. 햄 샌드위치를 구성하는 빵 두 개와 햄 한 개는 3차원의 측정 가능한 물체이며, 모두 합해 3개이기에 ‘단 한 번의 칼질(2차원 평면)’로 반으로 나누는 것이 가능한 것이다.
피자 공평하게 나누어 먹기
대부분의 피자는 8조각으로 나누어져 있는데, 동그란 피자의 정확한 가운데 점을 지나도록 칼로 자르면서 각각의 조각이 이루는 각도도 똑같이 한다면 피자 한 조각의 크기는 모두 같을 것이다. 하지만 시켜 놓은 피자가 정중앙에서 잘리지 않는 일이 빈번하다. 그렇다면 이미 조각이 나 있는 피자는 어떻게 나누어 먹을까? 간단한 방법은 나누어진 조각을 다시 반으로 잘 나누어 먹는 일이다. 하지만 피자가 어떤 점에서 8조각으로 나누어져 있더라도 각도가 똑같게 나누어져 있다면, 다시 자르지 않고도 두 사람이 똑같이 나누어 먹을 수 있다. ‘피자 정리(Pizza Theorem)’라고 이름 붙여진 이 정리는 어느 점에서든 같은 각도(45°)를 가지면서 8조각으로 나뉜 피자를 두 사람이 한 조각씩 번갈아 가며 먹으면 두 사람이 같은 양의 피자를 먹는다고 말하고 있다.
아래 그림은 8조각 난 피자를 한 조각씩 나누어 먹었을 때, 실제로 같은 양을 먹는지를 보여주는 것으로 1994년에 카터(Carter)와 왜건(Wagon) 이 증명한 것이다(영어 알파벳의 대문자와 소문자가 서로 대응되는 것에 집중해 보라). ‘피자 정리’에 따르면 이렇게 나누어 먹는 것은 두 명뿐 아니라, 여러 명인 경우에도 가능하다.
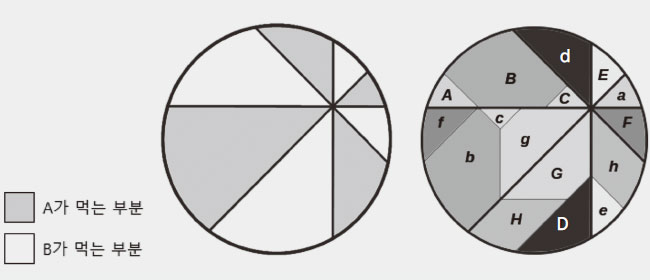
두 명인 경우 8조각을 내었지만, 세 명이라면 12조각, 네 명이라면 16조각 등 인원수에 4를 곱한 수만큼 자른 뒤 하나씩 번갈아 가며 먹으면 먹는 양이 모두 같다. 단, 이때 피자를 자르는 모든 선은 하나의 점에서 만나야 하며, 각각의 조각들이 점에서 이루는 각도는 모두 일정해야 한다.
현실적인 분배, 분할 선택법
빵이나 피자를 둘이서 나누어 먹을 때, 어느 부분을 자르면 정확히 두 부분의 크기가 같겠지만 현실적으로는 오차로 인해 정확하게 두 부분으로 나누기가 힘들다. 그렇다면 어떻게 해야 싸움이 나지 않을까? 정확하게 자르지 않아도 두 사람을 만족시키는 방법이 있는데, 바로 분할 선택법(Divide and Choose)이다.
A, B 두 사람이 있을 때, 한 사람(A)은 물건을 분할하는 사람이 되고 다른 사람(B)은 선택하는 사람이 되는 방법이다. A가 케이크를 ‘절반’으로 나누면 A는 두 조각 중 어느 조각을 먹어도 만족할 것이다. A가 자르고 난 후, B가 먼저 두 조각 중 본인이 보기에 큰 조각을 먹으면 A와 B 두 사람 모두 만족하게 된다. 3명 이상의 인원에서도 분할 선택법은 여전히 유효하지만 분할자와 선택자의 역할에 따라 방법이 조금씩 달라진다. 다음은 3명이 케이크를 나누어 가질 때, 각각 다른 분할 선택법으로 시행한 것이다.
단독 분할자 방법
A, B, C 세 사람 중 한 사람이 분할자가 된 뒤, 나머지 두 사람이 선택자가 되는 방법이다. A가 분할자가 되어 케이크를 1/3이 되도록 자르면 A는 어떤 조각을 가져가도 만족할 테니, B와 C가 만족하면 모두 해결이 된다. 만약 B와 C가 서로 다른 조각을 원한다면 각자 하나씩 가져가고 남은 조각을 A가 가져가면 모두가 만족할 것이다. 하지만 서로 같은 조각을 원할 수도 있는데, 이런 경우 B와 C 두 사람이 원하지 않는 조각 하나를 A에게 준 뒤 두 사람이 다시 분할 선택법을 시행하면 된다.
단독 선택자 방법
A, B, C 세 사람 중 두 사람이 분할자가 된 뒤, 나머지 한 사람이 선택자가 되는 방법이다. 먼저 A와 B는 두 명일 때의 분할 선택방법을 통해 두 조각으로 나누어 가진다. A와 B는 각자 가져간 조각을 1/3씩 나누어 놓고, 선택자 C는 A가 나누어 놓은 3조각 중 하나와 B가 나누어 놓은 3조각 중 하나를 가져간다. A와 B는 본인들의 기준에 만족하도록 1/3씩 분할하였으니 만족하고, C는 가장 먼저 선택했기에 만족한다.
마지막 감축자 방법
A, B, C 모두가 분할자이며 선택자가 되는 방법이다. 먼저 A가 케이크를 1/3로 자른 뒤, 나머지 사람에게 동의를 구한다(이 조각을 a라 하자). 이때, 모두가 동의한다면 A는 조각 a를 가지며, 동의하지 않는 사람(B)이 있다면 B는 조각 a를 ‘B가 생각하는 1/3조각’(b)으로 다시 자른 뒤 남은 한 사람(C)에게 동의를 구한다. C가 동의한다면 B는 조각 b를 가지면 되고, C가 동의하지 않는다면 B가 자른 조각을 ‘C가 생각하는 1/3조각’으로 잘라 가지면 된다. 먼저 자른 사람들은 나중에 자른 사람이 본인들이 생각했던 1/3조각보다 더 작게 가져가는 데에 만족할 것이기 때문이다.
나눌 수 없는 것을 분배해야 한다면?
피자, 케이크 같은 것은 정확히 자르거나, 분할 선택법을 통해 조각을 잘라 내어 분배를 할 수 있었다. 하지만 집과 같이 나눌 수 없는 물건이거나, 보석처럼 조각냈을 때 가치가 크게 떨어지는 물건이라면 어떻게 분배해야 할까? 이런 경우 봉인된 입찰법(The method of sealed bids)을 통해 물건을 분배하는데, 총 3단계로 진행된다.
① 참가자는 물건 각각에 대해 자신이 생각하는 가치를 적어 입찰한다. 입찰이 끝나면 각자의 입찰 금액을 모두 더한 뒤, 인원수로 다시 나누어 각자의 몫을 구한다.
② 각각의 항목에 대해 가장 높은 금액을 적은 사람은 해당 물건을 분배받는다. 자신의 몫보다 높은 가치를 배당 받았다면 차액을 지불하며, 자신의 몫보다 낮은 가치를 배당받았다면 차액을 현금으로 배당받는다.
③ ②에서 모인 차액이 부족한 이에게 배당되고 난 뒤, 남았다면 입찰에 참가한 인원수로 나누어 재분배한다.
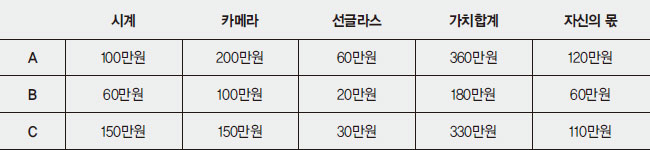
A, B, C 세 명이 시계, 카메라, 선글라스 세 개를 나누어 가지기 위해 봉인된 입찰법을 진행한다고 해 보자. 다음은 A, B, C가 각자 세 개의 물건에 대해 자신이 생각하는 가치로 입찰한 결과를 표로 정리한 것이다.
입찰 결과 시계에 가장 가치를 높게 둔 사람은 C이며, 카메라와 선글라스는 A가 가장 높게 가치를 두었다. 그 결과 C는 시계를 배당받는데, C가 생각하는 시계의 가치는 150만원이며 자신의 몫은 110만원이므로 차액인 40만원을 지불한다. 마찬가지로 A는 카메라와 선글라스의 가치 260만원과 자신의 몫 120만원의 차액인 140만원을 지불하며, 아무것도 받지 못한 B는 60만원을 현금으로 배당받는다. C와 A가 낸 금액과 B가 받은 금액을 정리하면 40만원+140만원-60만원=120만원이 되는데, 이 금액을 세 명이서 40만원씩 나눠 받으면 분배가 완료된다. 각자 자신이 생각하는 세 개의 물건 가치의 1/3만큼 배당을 받았으므로, 물질적인 측면에서는 공평하게 분배가 된 셈이다. 단, 봉인된 입찰법에 대해서는 다음과 같이 몇 가지 전제조건이 필요하다.
① 모든 입찰자는 충분한 돈을 소지해야 한다(차액을 현금으로 지불해야 하기 때문이다).
② 모든 입찰자는 현금이 물건에 대한 대체재로 작용한다는 것에 동의해야 한다.
③ 모든 입찰자들은 각자가 물건에 부여한 가치체계에 대해 서로 정보를 교환하는 등의 행위가 없어야 한다.
분배하는 게 항상 옳을까?
솔로몬의 이야기에서도 우리는 공평한 분배에 대한 것을 볼 수 있다. 한 아이를 두고 두 여인이 서로 자신의 아들이라고 주장하자, 솔로몬은 두 여인에게 아이를 둘로 나누어 가지라고 한다. 이에 한 여인은 그렇게 해서라도 아이를 갖겠다고 하고, 다른 여인은 아이를 포기하기에 이르며 솔로몬은 아이를 포기한 여인이 진짜 엄마라고 말하는 대목이다.
봉인된 입찰법에서 입찰자들이 서로 물건에 대해 다른 가치를 책정하듯, 진짜 엄마는 아이를 그 어떤 것으로도 대체 불가능한 존재로 생각했기에 아이가 죽는 것보다는 본인이 포기하는 쪽을 선택했을 것이다. 비단 사람의 목숨만이 아니라 물건에도 돈으로 환산하지 못할 가치가 있으니, 나누어 갖는 것이 능사가 아니라 진정한 가치를 찾는 것에 목표를 두어야 할 것이다.
사과나무 한 그루 겨우 심어져 있는 조그마한 땅을 형제가 서로 나누어 가지는 것보다는 나무를 함께 키우고 그 결실인 사과를 함께 먹는 것이 더욱 가치 있는 일이 아닐까 싶다.⊙
예전에 잠시 언급했던 부분이지만 우리 생활에 있는 대부분의 것들은 ‘연속적’인 물체들로 위와 같은 모양의 빵도 마찬가지다. 빵이 연속적인 물체이기 때문에, 어느 한쪽부터 선을 그어 두 부분의 넓이를 비교해 보면 그 비율이 어느 순간 5대5가 되는 경우가 반드시 생기며 그때 빵을 잘라 두 사람에게 나누어 주면 된다. 그렇다면 두 개의 빵 사이에 햄이 끼워져 있는 ‘햄 샌드위치’는 빵과 햄을 모두 펼쳐 놓은 뒤, 각각 반으로 자르고 다시 합쳐야 할까?폴란드의 유명한 수학자인 바나흐(Stefan Banach)에 의해 증명된 ‘햄 샌드위치 정리’는 ‘한 번의 칼질’로 햄 샌드위치를 정확히 반으로 자르는 것이 가능하다고 이야기한다. ‘햄 샌드위치 정리’는 일반적인 n차원에 대해서도 적용 가능한데, ‘n차원의 측정 가능한 물체 n개는 (n-1)차원의 평면 한 개로 각각의 물체를 정확히 이등분할 수 있다’는 게 그 내용이다. 햄 샌드위치를 구성하는 빵 두 개와 햄 한 개는 3차원의 측정 가능한 물체이며, 모두 합해 3개이기에 ‘단 한 번의 칼질(2차원 평면)’로 반으로 나누는 것이 가능한 것이다.
피자 공평하게 나누어 먹기
대부분의 피자는 8조각으로 나누어져 있는데, 동그란 피자의 정확한 가운데 점을 지나도록 칼로 자르면서 각각의 조각이 이루는 각도도 똑같이 한다면 피자 한 조각의 크기는 모두 같을 것이다. 하지만 시켜 놓은 피자가 정중앙에서 잘리지 않는 일이 빈번하다. 그렇다면 이미 조각이 나 있는 피자는 어떻게 나누어 먹을까? 간단한 방법은 나누어진 조각을 다시 반으로 잘 나누어 먹는 일이다. 하지만 피자가 어떤 점에서 8조각으로 나누어져 있더라도 각도가 똑같게 나누어져 있다면, 다시 자르지 않고도 두 사람이 똑같이 나누어 먹을 수 있다. ‘피자 정리(Pizza Theorem)’라고 이름 붙여진 이 정리는 어느 점에서든 같은 각도(45°)를 가지면서 8조각으로 나뉜 피자를 두 사람이 한 조각씩 번갈아 가며 먹으면 두 사람이 같은 양의 피자를 먹는다고 말하고 있다.
아래 그림은 8조각 난 피자를 한 조각씩 나누어 먹었을 때, 실제로 같은 양을 먹는지를 보여주는 것으로 1994년에 카터(Carter)와 왜건(Wagon) 이 증명한 것이다(영어 알파벳의 대문자와 소문자가 서로 대응되는 것에 집중해 보라). ‘피자 정리’에 따르면 이렇게 나누어 먹는 것은 두 명뿐 아니라, 여러 명인 경우에도 가능하다.
두 명인 경우 8조각을 내었지만, 세 명이라면 12조각, 네 명이라면 16조각 등 인원수에 4를 곱한 수만큼 자른 뒤 하나씩 번갈아 가며 먹으면 먹는 양이 모두 같다. 단, 이때 피자를 자르는 모든 선은 하나의 점에서 만나야 하며, 각각의 조각들이 점에서 이루는 각도는 모두 일정해야 한다.
현실적인 분배, 분할 선택법
빵이나 피자를 둘이서 나누어 먹을 때, 어느 부분을 자르면 정확히 두 부분의 크기가 같겠지만 현실적으로는 오차로 인해 정확하게 두 부분으로 나누기가 힘들다. 그렇다면 어떻게 해야 싸움이 나지 않을까? 정확하게 자르지 않아도 두 사람을 만족시키는 방법이 있는데, 바로 분할 선택법(Divide and Choose)이다.
A, B 두 사람이 있을 때, 한 사람(A)은 물건을 분할하는 사람이 되고 다른 사람(B)은 선택하는 사람이 되는 방법이다. A가 케이크를 ‘절반’으로 나누면 A는 두 조각 중 어느 조각을 먹어도 만족할 것이다. A가 자르고 난 후, B가 먼저 두 조각 중 본인이 보기에 큰 조각을 먹으면 A와 B 두 사람 모두 만족하게 된다. 3명 이상의 인원에서도 분할 선택법은 여전히 유효하지만 분할자와 선택자의 역할에 따라 방법이 조금씩 달라진다. 다음은 3명이 케이크를 나누어 가질 때, 각각 다른 분할 선택법으로 시행한 것이다.
단독 분할자 방법
A, B, C 세 사람 중 한 사람이 분할자가 된 뒤, 나머지 두 사람이 선택자가 되는 방법이다. A가 분할자가 되어 케이크를 1/3이 되도록 자르면 A는 어떤 조각을 가져가도 만족할 테니, B와 C가 만족하면 모두 해결이 된다. 만약 B와 C가 서로 다른 조각을 원한다면 각자 하나씩 가져가고 남은 조각을 A가 가져가면 모두가 만족할 것이다. 하지만 서로 같은 조각을 원할 수도 있는데, 이런 경우 B와 C 두 사람이 원하지 않는 조각 하나를 A에게 준 뒤 두 사람이 다시 분할 선택법을 시행하면 된다.
단독 선택자 방법
A, B, C 세 사람 중 두 사람이 분할자가 된 뒤, 나머지 한 사람이 선택자가 되는 방법이다. 먼저 A와 B는 두 명일 때의 분할 선택방법을 통해 두 조각으로 나누어 가진다. A와 B는 각자 가져간 조각을 1/3씩 나누어 놓고, 선택자 C는 A가 나누어 놓은 3조각 중 하나와 B가 나누어 놓은 3조각 중 하나를 가져간다. A와 B는 본인들의 기준에 만족하도록 1/3씩 분할하였으니 만족하고, C는 가장 먼저 선택했기에 만족한다.
마지막 감축자 방법
A, B, C 모두가 분할자이며 선택자가 되는 방법이다. 먼저 A가 케이크를 1/3로 자른 뒤, 나머지 사람에게 동의를 구한다(이 조각을 a라 하자). 이때, 모두가 동의한다면 A는 조각 a를 가지며, 동의하지 않는 사람(B)이 있다면 B는 조각 a를 ‘B가 생각하는 1/3조각’(b)으로 다시 자른 뒤 남은 한 사람(C)에게 동의를 구한다. C가 동의한다면 B는 조각 b를 가지면 되고, C가 동의하지 않는다면 B가 자른 조각을 ‘C가 생각하는 1/3조각’으로 잘라 가지면 된다. 먼저 자른 사람들은 나중에 자른 사람이 본인들이 생각했던 1/3조각보다 더 작게 가져가는 데에 만족할 것이기 때문이다.
나눌 수 없는 것을 분배해야 한다면?
피자, 케이크 같은 것은 정확히 자르거나, 분할 선택법을 통해 조각을 잘라 내어 분배를 할 수 있었다. 하지만 집과 같이 나눌 수 없는 물건이거나, 보석처럼 조각냈을 때 가치가 크게 떨어지는 물건이라면 어떻게 분배해야 할까? 이런 경우 봉인된 입찰법(The method of sealed bids)을 통해 물건을 분배하는데, 총 3단계로 진행된다.
① 참가자는 물건 각각에 대해 자신이 생각하는 가치를 적어 입찰한다. 입찰이 끝나면 각자의 입찰 금액을 모두 더한 뒤, 인원수로 다시 나누어 각자의 몫을 구한다.
② 각각의 항목에 대해 가장 높은 금액을 적은 사람은 해당 물건을 분배받는다. 자신의 몫보다 높은 가치를 배당 받았다면 차액을 지불하며, 자신의 몫보다 낮은 가치를 배당받았다면 차액을 현금으로 배당받는다.
③ ②에서 모인 차액이 부족한 이에게 배당되고 난 뒤, 남았다면 입찰에 참가한 인원수로 나누어 재분배한다.
A, B, C 세 명이 시계, 카메라, 선글라스 세 개를 나누어 가지기 위해 봉인된 입찰법을 진행한다고 해 보자. 다음은 A, B, C가 각자 세 개의 물건에 대해 자신이 생각하는 가치로 입찰한 결과를 표로 정리한 것이다.
입찰 결과 시계에 가장 가치를 높게 둔 사람은 C이며, 카메라와 선글라스는 A가 가장 높게 가치를 두었다. 그 결과 C는 시계를 배당받는데, C가 생각하는 시계의 가치는 150만원이며 자신의 몫은 110만원이므로 차액인 40만원을 지불한다. 마찬가지로 A는 카메라와 선글라스의 가치 260만원과 자신의 몫 120만원의 차액인 140만원을 지불하며, 아무것도 받지 못한 B는 60만원을 현금으로 배당받는다. C와 A가 낸 금액과 B가 받은 금액을 정리하면 40만원+140만원-60만원=120만원이 되는데, 이 금액을 세 명이서 40만원씩 나눠 받으면 분배가 완료된다. 각자 자신이 생각하는 세 개의 물건 가치의 1/3만큼 배당을 받았으므로, 물질적인 측면에서는 공평하게 분배가 된 셈이다. 단, 봉인된 입찰법에 대해서는 다음과 같이 몇 가지 전제조건이 필요하다.
① 모든 입찰자는 충분한 돈을 소지해야 한다(차액을 현금으로 지불해야 하기 때문이다).
② 모든 입찰자는 현금이 물건에 대한 대체재로 작용한다는 것에 동의해야 한다.
③ 모든 입찰자들은 각자가 물건에 부여한 가치체계에 대해 서로 정보를 교환하는 등의 행위가 없어야 한다.
분배하는 게 항상 옳을까?
솔로몬의 이야기에서도 우리는 공평한 분배에 대한 것을 볼 수 있다. 한 아이를 두고 두 여인이 서로 자신의 아들이라고 주장하자, 솔로몬은 두 여인에게 아이를 둘로 나누어 가지라고 한다. 이에 한 여인은 그렇게 해서라도 아이를 갖겠다고 하고, 다른 여인은 아이를 포기하기에 이르며 솔로몬은 아이를 포기한 여인이 진짜 엄마라고 말하는 대목이다.
봉인된 입찰법에서 입찰자들이 서로 물건에 대해 다른 가치를 책정하듯, 진짜 엄마는 아이를 그 어떤 것으로도 대체 불가능한 존재로 생각했기에 아이가 죽는 것보다는 본인이 포기하는 쪽을 선택했을 것이다. 비단 사람의 목숨만이 아니라 물건에도 돈으로 환산하지 못할 가치가 있으니, 나누어 갖는 것이 능사가 아니라 진정한 가치를 찾는 것에 목표를 두어야 할 것이다.
사과나무 한 그루 겨우 심어져 있는 조그마한 땅을 형제가 서로 나누어 가지는 것보다는 나무를 함께 키우고 그 결실인 사과를 함께 먹는 것이 더욱 가치 있는 일이 아닐까 싶다.⊙
월간조선
댓글 없음:
댓글 쓰기