정사각형이나 정해진 모양으로 배열된 수들에서는 좌우대각의 균형을 이루는 법칙
⊙ 중국 하나라 우 임금이 발견한 ‘낙도(洛圖)’, 뒤러의 그림 〈멜랑콜리아〉 등에서 발견
⊙ 조선시대 최석정의 저서 《구수략》에도 특수 마방진인 ‘지수귀문도’ 소개
⊙ 중국 하나라 우 임금이 발견한 ‘낙도(洛圖)’, 뒤러의 그림 〈멜랑콜리아〉 등에서 발견
⊙ 조선시대 최석정의 저서 《구수략》에도 특수 마방진인 ‘지수귀문도’ 소개
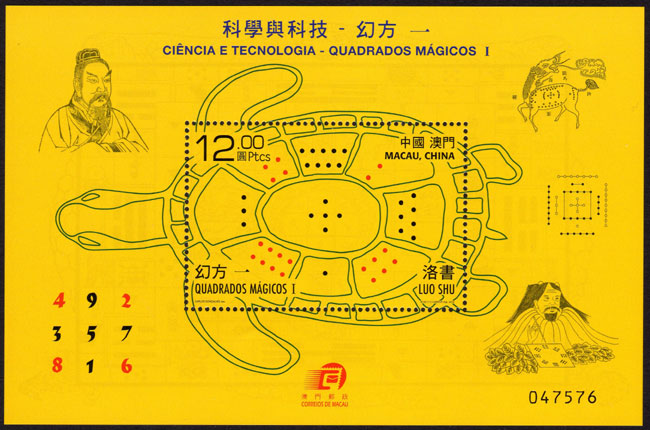
- 마카오 발행 마방진 우표(2014년).
지금으로부터 약 3000년 전, 중국 하(夏)나라의 우(禹) 임금은 황하의 잦은 범람을 막기 위해 치수(治水) 공사를 하다가 거북의 등 껍데기에 이상한 그림이 새겨진 것을 발견했다. 점 45개로 이루어진 이 그림을 들여다보면 1부터 9까지의 자연수가 점의 개수로 나타나 있는데 이 수들의 배열은 가로, 세로, 대각선으로 더했을 때 합이 항상 15로 같았다. 사람들은 이 배열을 신비로워하여 낙도(洛圖), 하도(河圖), 낙서(洛書) 등이라 부르며 우주의 비밀을 담고 있고, 음양오행의 원리를 함축한다고 여겼다. 사람들은 이것의 원리를 연구하여 동양에서 가장 오래된 경전 중 하나이자 인간과 자연의 근본 양상을 설명하는 《주역(周易)》으로 발전시키기도 했다.
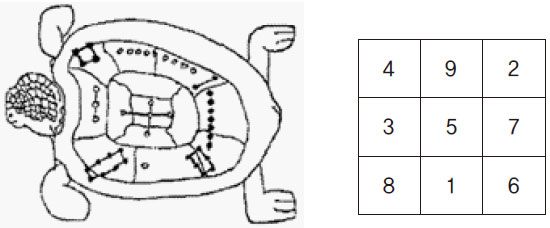
이렇게 9개의 수부터 수십만 자리의 연속되는 수까지 정사각형이나 정해진 모양으로 배열된 수들에는 좌우대각의 균형을 이루는 법칙이 있는데 서양에서는 마법의 사각형(magic square)이라고 하고 동양에서는 마방진(魔方陣)이라고 한다. ‘마술적인 정사각형 숫자 배열’이라는 뜻으로 ‘마법진(魔法陣)’이라고도 한다.
마방진은 1부터 n2까지의 연속된 자연수를 행, 열, 대각선의 합이 같도록 정사각형 모양(n×n 행렬)으로 배열한 것을 의미한다. 정사각형의 한 변에 배열된 수의 개수에 따라 3차 마방진, 4차 마방진 등이라고 부르는데 이때 한 열의 합은 3차 마방진에서는 15, 4차 마방진에서는 34, 5차 마방진에서는 65가 되며 n차 마방진에서는 n(n2+1)/2 가 된다. 이는 1부터 n열까지의 수를 모두 더하면 1부터 n2까지의 수의 합인 n(n2+1)/2가 되고 각 열의 합은 이것을 n으로 나눈 값이 되기 때문이다.
마방진 연구의 역사
중국에서 마방진이 처음으로 등장한 책은 송(宋)나라 양휘의 저서 《양휘산법》(1275)이다. 이 책에서는 3차 마방진부터 8차 마방진까지 다루고 명나라의 정대위(程大位)는 《산법통종(算法統宗) 》(1593)을 통해 10차 마방진까지 그 원리를 밝혀 내고 있다.
중국의 마방진은 아라비아 상인들을 통해 인도, 페르시아, 유럽으로 전해져 서양에서 많은 연구가 진행되었다. 유럽인들 역시 마방진을 신비롭게 여겨 은판에 새겨서 전쟁이나 질병으로부터의 안전을 기원하는 부적으로 사용하였다. 서양에서의 최초 마방진은 독일 기하학자이자 화가인 알브레히트 뒤러(1471~1528)의 동판화 작품인 〈멜랑콜리아〉 속에 있는 4차 마방진이다. 이 마방진의 맨 아래 줄의 중간에 있는 두 숫자 15, 14는 이 그림이 그려진 연도인 1514를 의미한다. 당시 서양에서는 마방진을 우주의 원리를 이용한 점성술에 사용해 왔는데 3차 마방진은 토성, 4차 마방진은 목성, 5차 마방진은 화성, 6차 마방진은 태양, 7차 마방진은 금성, 8차 마방진은 수성, 9차 마방진은 달과 연결시켰다. 이 작품에서는 당시의 마방진에 대한 인식이 표현되어 있다. 제목인 ‘멜랑콜리아’는 라틴어로 우울이라는 뜻을 가지고 있고 개, 박쥐, 해골 등과 같은 물체 역시 우울한 성질을 의미하는데 이는 모두 3차 마방진인 토성에 해당한다. 한편, 르네상스 시대의 예술가들은 수학에서 많은 영감을 받아 작품활동을 하였는데 이 작품에도 컴퍼스, 저울, 자, 모래시계, 구, 다각형 등이 나타난다. 특히 냉철함을 상징하는 목성에 해당하는 4차 마방진은 그림 전반에서 나타나는 우울함을 치료하는 부적의 의미로 사용되었다.
뒤러의 4차 마방진은 이후 서양에서 많은 연구가 이루어졌는데 B. 프레니클은 1693년 뒤러의 마방진 해법이 총 880개라는 것을 처음으로 밝혀 내기도 했다.
마방진을 구하는 방법
지금까지의 연구 결과는 모든 수에 대한 마방진이 존재하지만 2차 마방진은 존재하지 않는 것으로 밝혀졌다. 1, 2, 3, 4를 한 번씩만 써서 상하좌우, 대각선 방향의 숫자의 합을 같게 할 수 없다. 차수가 홀수인 경우 홀수 마방진, 짝수인 경우 짝수 마방진이라고 하는데 구하는 방법은 다음과 같다.
홀수 마방진
홀수 마방진은 아래와 같은 방법으로 구할 수 있다.
(1) 1행의 중앙에 1을 적는다.
(2) 우측 상단의 대각선 방향으로 2부터 자연수를 차례로 적는다.
(3) (2)의 방향으로 진행하다가 정사각형을 위쪽으로 넘어가면 그 열의 마지막 행으로 이동하여 해당 수를 쓰고 계속 진행한다.
(4) (2)의 방향으로 진행하다가 정사각형의 오른쪽으로 넘어가면 그 행의 1열로 이동하여 해당 수를 쓰고 계속 진행한다.
(5) n차 마방진에서 n의 배수까지 적으면 대각선 방향에 이미 수가 있으므로, 바로 아래 칸으로 이동하여 계속 진행한다.
(6) 1행 n열에 이르면 바로 아래 칸에 적는다.
짝수 마방진
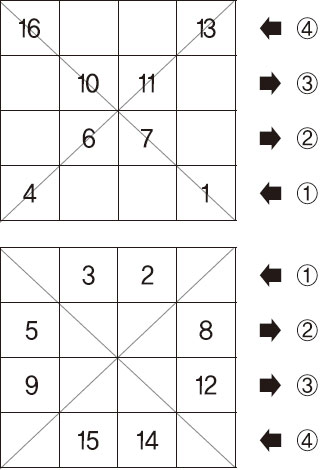
짝수 마방진을 만드는 일반적인 규칙은 없으나 A. 뒤러의 4차 마방진을 구하는 방법은 다음과 같다.
(1) 양쪽 대각선이 지나는 칸에 4행부터 다음 규칙에 따라 수를 적는다.
1부터 16까지의 수를 우측 하단부터 시작하여 각 행을 화살표의 방향대로 대각선이 표시된 칸에만 쓴다.
(2) 같은 방법으로 1행에서 시작하여 화살표 방향에 따라 순서대로 남은 8개의 칸에 해당되는 숫자를 쓴다.
(3) (1)과 (2)의 결과 값을 합한다.
특수 마방진
정사각형 형태의 마방진과는 모양은 다르지만 삼각형, 육각형, 원형 등 다양한 숫자 배열에서도 규칙이 나타나는 특수 마방진도 있다.
프랭클린 마방진
벤저민 프랭클린(1706~1790)은 미국 독립의 영웅이자 번개가 전기라는 것을 증명하고 피뢰침을 발명한 인물로 정치뿐만 아니라 외교, 언론, 과학 분야에서도 많은 활동을 했었다. 프랭클린은 8차 마방진을 만들고 자신의 이름을 붙여 ‘프랭클린 마방진’이라고 명명했다.
8차 마방진은 8(82+1)/2=260으로 이 마방진에서의 각 행의 수의 합과 각 열의 수의 합은 260이 된다. 그러나 대각선의 수의 합은 260이 되지 않는다. 다만, 같은 색으로 이루어진 대각선 위의 수들의 합을 구해 보면 260이 되는 특수성을 가진다.
지수귀문도
지수귀문도란 동양 전래의 수학과 철학을 담은 숫자놀이 같은 것으로 생긴 모양이 거북의 등과 같아 보여 붙여진 이름이다. 이는 조선 숙종 때 영의정을 지낸 최석정(1646~1715)의 저서 《구수략》에 있는 특수 마방진으로 아홉 개의 육각형이 거북등 모양처럼 연결되어 있으며, 육각형의 꼭짓점에 1부터 30까지의 수를 배치하여 각 육각형을 이루는 여섯 개 수의 합이 모두 93으로 같도록 만들어져 있다. 이 수들을 조합을 다르게 하면 그 합이 93이 아닌 77~109까지 다른 결과가 나오게 할 수도 있다.
이것을 변형하여 육각형 네 개가 마름모꼴을 이루어 꼭짓점에 1에서 16까지의 수를 채우는 모양도 있다. 이 경우 각 육각형의 합은 40부터 62까지 가능하며, 모두 687,851,136개가 존재하는 것으로 알려져 있다.⊙

이렇게 9개의 수부터 수십만 자리의 연속되는 수까지 정사각형이나 정해진 모양으로 배열된 수들에는 좌우대각의 균형을 이루는 법칙이 있는데 서양에서는 마법의 사각형(magic square)이라고 하고 동양에서는 마방진(魔方陣)이라고 한다. ‘마술적인 정사각형 숫자 배열’이라는 뜻으로 ‘마법진(魔法陣)’이라고도 한다.
마방진은 1부터 n2까지의 연속된 자연수를 행, 열, 대각선의 합이 같도록 정사각형 모양(n×n 행렬)으로 배열한 것을 의미한다. 정사각형의 한 변에 배열된 수의 개수에 따라 3차 마방진, 4차 마방진 등이라고 부르는데 이때 한 열의 합은 3차 마방진에서는 15, 4차 마방진에서는 34, 5차 마방진에서는 65가 되며 n차 마방진에서는 n(n2+1)/2 가 된다. 이는 1부터 n열까지의 수를 모두 더하면 1부터 n2까지의 수의 합인 n(n2+1)/2가 되고 각 열의 합은 이것을 n으로 나눈 값이 되기 때문이다.
마방진 연구의 역사
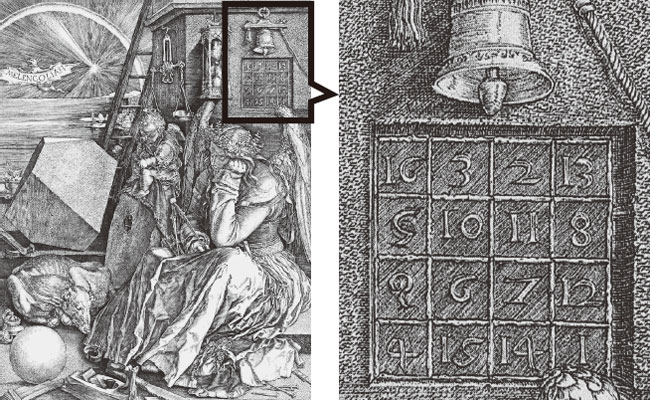 |
| 독일 화가 뒤러의 동판화 〈멜랑콜리아〉에 등장한 마방진. |
중국의 마방진은 아라비아 상인들을 통해 인도, 페르시아, 유럽으로 전해져 서양에서 많은 연구가 진행되었다. 유럽인들 역시 마방진을 신비롭게 여겨 은판에 새겨서 전쟁이나 질병으로부터의 안전을 기원하는 부적으로 사용하였다. 서양에서의 최초 마방진은 독일 기하학자이자 화가인 알브레히트 뒤러(1471~1528)의 동판화 작품인 〈멜랑콜리아〉 속에 있는 4차 마방진이다. 이 마방진의 맨 아래 줄의 중간에 있는 두 숫자 15, 14는 이 그림이 그려진 연도인 1514를 의미한다. 당시 서양에서는 마방진을 우주의 원리를 이용한 점성술에 사용해 왔는데 3차 마방진은 토성, 4차 마방진은 목성, 5차 마방진은 화성, 6차 마방진은 태양, 7차 마방진은 금성, 8차 마방진은 수성, 9차 마방진은 달과 연결시켰다. 이 작품에서는 당시의 마방진에 대한 인식이 표현되어 있다. 제목인 ‘멜랑콜리아’는 라틴어로 우울이라는 뜻을 가지고 있고 개, 박쥐, 해골 등과 같은 물체 역시 우울한 성질을 의미하는데 이는 모두 3차 마방진인 토성에 해당한다. 한편, 르네상스 시대의 예술가들은 수학에서 많은 영감을 받아 작품활동을 하였는데 이 작품에도 컴퍼스, 저울, 자, 모래시계, 구, 다각형 등이 나타난다. 특히 냉철함을 상징하는 목성에 해당하는 4차 마방진은 그림 전반에서 나타나는 우울함을 치료하는 부적의 의미로 사용되었다.
뒤러의 4차 마방진은 이후 서양에서 많은 연구가 이루어졌는데 B. 프레니클은 1693년 뒤러의 마방진 해법이 총 880개라는 것을 처음으로 밝혀 내기도 했다.
마방진을 구하는 방법
지금까지의 연구 결과는 모든 수에 대한 마방진이 존재하지만 2차 마방진은 존재하지 않는 것으로 밝혀졌다. 1, 2, 3, 4를 한 번씩만 써서 상하좌우, 대각선 방향의 숫자의 합을 같게 할 수 없다. 차수가 홀수인 경우 홀수 마방진, 짝수인 경우 짝수 마방진이라고 하는데 구하는 방법은 다음과 같다.
홀수 마방진
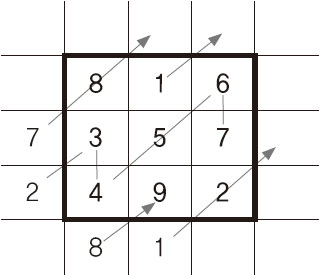 |
| 3차 마방진 구하는 방법. |
(1) 1행의 중앙에 1을 적는다.
(2) 우측 상단의 대각선 방향으로 2부터 자연수를 차례로 적는다.
(3) (2)의 방향으로 진행하다가 정사각형을 위쪽으로 넘어가면 그 열의 마지막 행으로 이동하여 해당 수를 쓰고 계속 진행한다.
(4) (2)의 방향으로 진행하다가 정사각형의 오른쪽으로 넘어가면 그 행의 1열로 이동하여 해당 수를 쓰고 계속 진행한다.
(5) n차 마방진에서 n의 배수까지 적으면 대각선 방향에 이미 수가 있으므로, 바로 아래 칸으로 이동하여 계속 진행한다.
(6) 1행 n열에 이르면 바로 아래 칸에 적는다.
짝수 마방진

짝수 마방진을 만드는 일반적인 규칙은 없으나 A. 뒤러의 4차 마방진을 구하는 방법은 다음과 같다.
(1) 양쪽 대각선이 지나는 칸에 4행부터 다음 규칙에 따라 수를 적는다.
1부터 16까지의 수를 우측 하단부터 시작하여 각 행을 화살표의 방향대로 대각선이 표시된 칸에만 쓴다.
(2) 같은 방법으로 1행에서 시작하여 화살표 방향에 따라 순서대로 남은 8개의 칸에 해당되는 숫자를 쓴다.
(3) (1)과 (2)의 결과 값을 합한다.
특수 마방진
정사각형 형태의 마방진과는 모양은 다르지만 삼각형, 육각형, 원형 등 다양한 숫자 배열에서도 규칙이 나타나는 특수 마방진도 있다.
프랭클린 마방진
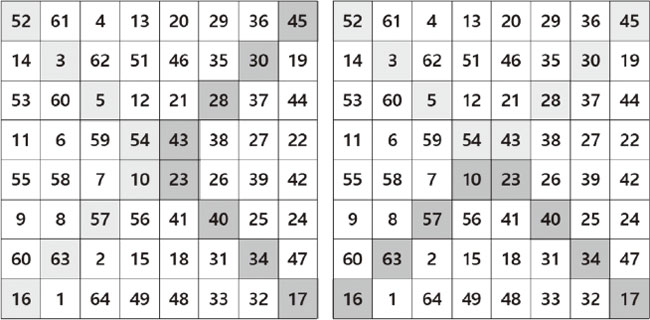 |
| 같은 색으로 이루어진 대각선의 합이 같은 프랭클린 마방진. |
8차 마방진은 8(82+1)/2=260으로 이 마방진에서의 각 행의 수의 합과 각 열의 수의 합은 260이 된다. 그러나 대각선의 수의 합은 260이 되지 않는다. 다만, 같은 색으로 이루어진 대각선 위의 수들의 합을 구해 보면 260이 되는 특수성을 가진다.
지수귀문도
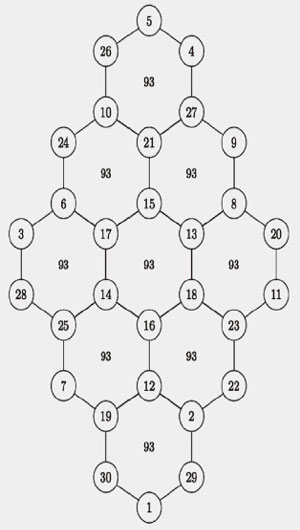 |
| 각 육각형의 합이 93인 지수귀문도. |
이것을 변형하여 육각형 네 개가 마름모꼴을 이루어 꼭짓점에 1에서 16까지의 수를 채우는 모양도 있다. 이 경우 각 육각형의 합은 40부터 62까지 가능하며, 모두 687,851,136개가 존재하는 것으로 알려져 있다.⊙
- 월간조선
댓글 없음:
댓글 쓰기