
- 만 5세가 채 되지 않은 아이들은 크기와 개수를 혼동하여 멀리 떨어뜨려 놓은 동전 2개가 더 많다고 대답한다.
유명한 유아~초등학생 수학교육서에 이런 대목이 있다. 그림과 같이 작은 동전 6개를 촘촘히 놓고, 큰 동전 2개를 멀리 놓은 뒤, 동전의 개수가 어느 쪽이 더 많냐고 묻는 장면이다.
만 5세가 채 되지 않은 아이들은 크기와 개수를 혼동하여 멀리 떨어뜨려 놓은 동전 2개가 더 많다고 대답한다. 성인이 된 우리는 크기에 혼동되지 않고, 개수에 집중하여 동전 6개와 동전 2개 중 6개가 더 많다는 것을 자연스럽고도 당연하게 알 수 있다.
우리가 사용하는 길이는 이상하다
수학 수업을 떠올려보면 수직선을 0부터 10까지 그은 뒤, 양 끝점을 모두 포함하는 것을 ‘닫힌 구간 [0, 10]’이라 하고, 양 끝점을 뺀 것을 ‘열린 구간 (0, 10)’이라고 배운 것을 기억할 것이다. 그렇다면 [0, 10]과 (0, 10)의 길이는 각각 몇이라고 하면 좋을까?
약간은 고민하겠지만 대부분 ‘10’이라고 대답할 것이다. 예전 기억을 떠올려보면 9.9999…=10이라고 했으니 (0, 10)과 [0, 10]의 길이는 같을 수도 있을 것 같다. 그런데 이렇게 생각하고 보니 [0, 10]은 [0, 1), [1, 2), … , [9, 10]이 모인 것이니 같은 방식으로 하면 0, 1, 2, … , 9, 10의 점들은 모두 빠져도 상관이 없어야 한다.
내친김에 더 작게 [0, ), [, ), … 으로 생각해 보면 [0, 10]까지의 숫자 중 , , … , ,까지 빠져도 되고, 숫자만 조절하면 어마어마한 개수의 점들이 빠질 수 있다는 것까지 생각이 이르게 된다. 이쯤 되니 우리가 길이를 제대로 재고 있긴 하나 라는 생각마저 들기도 한다.
길이는 어떻게 측정하는 것인가?
우리가 현재 사용하고 있는 길이, 무게, 크기 등에서 모두 위와 같은 현상이 나타난다. 그렇다면 우리가 무엇인가를 잘못하고 있는 것일까? 아님 무엇인가를 빼놓고 생각하는 것일까? 수학에서는 이런 것들을 엄밀하게 하기 위해서 ‘측도(measure)’라는 것을 정의하여 사용하고 있다. ‘측도’라는 것이 무엇인지 핵심적인 것만을 말하면 다음과 같다.
(1) 측도 함수 μ는 항상 0보다 크거나 같다.
(2) 아무것도 없는 집합의 측도 함숫값은 0이다.
(3) 어떤 집합 A를 측도 함수 μ로 측정한 값은 A를 서로 겹치지 않게 나눈 뒤, 각각을 잰 측정값을 더한 것과 같다.
이를 받아들이기 쉽게 길이에 빗대어 다시 말해보면 다음과 같다.
(1) 길이는 항상 0보다 크거나 같다.
(2) 아무것도 없는 것의 길이는 0이다.
(3) 어떤 물체 A의 길이는 그 물체를 겹치는 부분이 없게 길이를 나누어 잰 뒤 합한 것과 길이가 같다.

우리가 일반적으로 사용하는 ‘길이’와 같은 측도 함수는 르베그 측도 함수로, 이는 측도 이론에 큰 공헌을 한 앙리 르베그(Henri Lebesgue)에서 따온 것이다. 이제, 이를 가지고 [0, 10]의 길이를 측정해 보자.
그럼 대체 [0, 10]과 (0, 10)의 길이는 몇이라고 해야 할까?
결론부터 말을 하자면 당연히 10이다. 물론 ‘어떤’ 측도 함수를 사용했는지에 따라 다르지만 르베그 측도 함수로는 10이 나온다. 다음은 우리가 길이를 재기 위해 사용할 르베그 측도 함수의 정의이다.
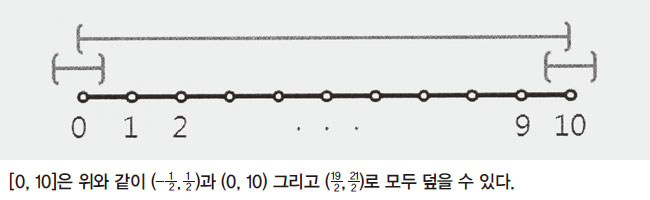
어려운 공식처럼 보이는 이것을 말로 풀어서 쓰면 ‘A를 모두 덮을 수 있도록 (겹치든 겹치지 않든) 열린 구간들을 모은 것들의 길이를 합한 것 중 최대 하계(하한)’가 된다. 하계란 어떤 수가 가질 수 있는 범위보다 작은 수로서, 만약 ‘x 〉 3’이라면 0과 3 모두 x가 될 수 있는 어떤 수보다도 작은 수이기에 하계이다. 하지만 3보다 큰 수들은 x가 될 수 있기에 3을 x의 최대 하계 또는 하한이라 부른다. 이제, 우리는 [0, 10]과 (0, 10)의 길이를 잴 준비가 되었다. 열린 구간 (0, 10)의 길이는 처음부터 열린 구간 그 자체이므로 하한 값은 자기 자신인 10이다. (열린 구간 (a, b)의 길이는 b-a로 정의한다.) 여기에 또한, [0, 10]의 닫힌 구간은 (-,)와 (0, 10), (,)로 덮을 수 있는데 이때의 각각의 길이 합은 1+10+1=12이지만 0과 10을 덮기 위해 추가한 (-,)와 (,)를 (-,)와 (,)로 바꿔도 모두 덮을 수 있으므로 0.2+10+0.2=10.4로 길이가 줄게 된다. 같은 방식으로 계속 길이를 줄여나갈 수 있지만 아무리 줄어들어도 10 이하로는 내려가지 않는다는 것을 알 수 있는데, 이렇게 더 이상 내려갈 수 없는 값들 중 가장 큰 값(여기서는 10)을 하한이라고 한다.
그런데 아직 의문은 풀리지 않았다. (0, 10)과 [0, 10]의 길이가 같다는 것은 알게 되었지만 그럼 ‘점을 몇 개나 빼도 길이가 같은 걸까?’라는 의문은 아직 풀리지 않은 것이다. 이에 대해서 이야기하려면 다분한 수학용어들이 등장하기에 간략히 하자면 ‘셀 수 있을 만큼 많이’ 점을 빼도 길이는 똑같다.
수학에서는 무한히 많은 것들에 대해서도 ‘셀 수 있을 만큼 많은’과 ‘셀 수 없을 만큼 많은’으로 경우를 나누는데, 분수 형태로 표시할 수 있는 유리수는 셀 수 있을 만큼 많은 경우며, 무리수의 개수는 셀 수 없을 만큼 많은 경우다. 따라서 [0, 10] 사이에 존재하는 모든 유리수를 모아서 르베그 측도로 길이를 재면 그 값은 0이 나오고, 무리수만 모아서 재도 0이 나온다. 이는 이해를 돕기 위해 예를 든 것으로, 셀 수 없이 많은 점을 모아 르베그 측도 값을 재도 0이 나오는 경우가 있음을 알아야 한다.
대체 무엇을 측정할 수 있을까?

수학이라는 것은 일반인이 보기에 살아가는 데 별 필요 없는 학문일지도 모른다. 지금까지 이야기한 측도에 관한 것도 쓰임새가 없다면 그렇게 보일지 모른다. 하지만 이러한 측도 이론은 현대를 살아가는 우리에게 너무나도 익숙한 확률과 큰 연관성이 있다. 러시아 수학자인 안드레이 니콜라에비치 콜모고로프(Andrey Nikolaevich Kolmogorov)는 독립적으로 연구되어 오던 측도 이론과 확률론을 결합하여 현대 확률론의 바탕을 마련했다. 확률에는 주사위의 1, 2, 3, 4, 5, 6처럼 값이 딱딱 떨어지는 표본이 있는 반면, 한 공장에서 만들어진 전구의 수명처럼 값이 떨어지는 것이 아닌 연속적으로 이어질 수 있는 경우가 있다. 예를 들어 전구의 수명이 5년 이상이라고 하는 것은 만들어지는 모든 전구의 수명이 5년 이상이라는 것이 아니라 수명이 5년 미만인 전구가 나올 확률이 0이라는 것이다. 콜모고로프 이전의 확률론은 주사위의 경우와 전구의 수명 같은 경우를 따로 계산했지만, 콜모고로프 이후의 확률론은 각 확률을 계산하는 변수의 ‘측도’를 달리하여 계산한다. 주사위의 경우 모든 경우를 ‘각각 세는 측도’이지만 전구 수명의 경우 ‘측도 함숫값이 0인 변수 부분은 제외’하고 계산하는 것이다. 콜모고로프 이후 많은 발전을 이룬 확률론은 경제, 통계학에 사용됨은 물론 현대물리의 정수라 불리는 양자역학 또한 ‘확률론적 결정론’이 적용된다.
‘확률이 0’≠‘불가능’?
소위 ‘확률이 0이다’라는 것을 ‘불가능하다’라는 것과 똑같다고 생각하지만 확률론에서는 두 가지를 서로 다르다고 정의한다. 다트 게임을 생각해 보자.
구역마다 정해진 점수가 있지만 구역을 나누는 경계선은 항상 논쟁거리인데, 일반적으로 경계선에 맞았을 경우 두 구역 중 높은 점수를 얻는 것으로 되어 있다. 만약 다트의 끝이 선과 같이 매우 가늘다면 다트가 경계선에 맞을 확률은 몇이나 될까? 르베그 측도에서 다시금 생각해 보면 다트 게임판에서 얇은 선이 차지하는 면적은 0이 되는데, 이를 바꾸어 말하면 다트로 선을 정확히 맞힐 확률은 0을 뜻하게 된다. 하지만 우리는 다트 게임 혹은 양궁에서 보듯이 불가능하지는 않다는 것을 몸으로 체감하고 있다.
손에서 떠나 표적 바로 앞까지 진행한 다트가 순간 사라진다거나 이미 맞은 위치가 바뀐다거나 하는 일은 ‘불가능’한 일이다.
어쩌면 이것이 의미하는 바가 리우올림픽에서 펜싱의 박상영 선수가 10-14로 몰린 상황에서 역전해 금메달을 차지한 것처럼 눈앞에 분명히 있지만 성공 확률이 매우 낮은 것도 노력하면 이룰 수 있다는 희망적인 메시지가 아닌가 하고 생각해 본다.⊙
만 5세가 채 되지 않은 아이들은 크기와 개수를 혼동하여 멀리 떨어뜨려 놓은 동전 2개가 더 많다고 대답한다. 성인이 된 우리는 크기에 혼동되지 않고, 개수에 집중하여 동전 6개와 동전 2개 중 6개가 더 많다는 것을 자연스럽고도 당연하게 알 수 있다.
우리가 사용하는 길이는 이상하다
수학 수업을 떠올려보면 수직선을 0부터 10까지 그은 뒤, 양 끝점을 모두 포함하는 것을 ‘닫힌 구간 [0, 10]’이라 하고, 양 끝점을 뺀 것을 ‘열린 구간 (0, 10)’이라고 배운 것을 기억할 것이다. 그렇다면 [0, 10]과 (0, 10)의 길이는 각각 몇이라고 하면 좋을까?
약간은 고민하겠지만 대부분 ‘10’이라고 대답할 것이다. 예전 기억을 떠올려보면 9.9999…=10이라고 했으니 (0, 10)과 [0, 10]의 길이는 같을 수도 있을 것 같다. 그런데 이렇게 생각하고 보니 [0, 10]은 [0, 1), [1, 2), … , [9, 10]이 모인 것이니 같은 방식으로 하면 0, 1, 2, … , 9, 10의 점들은 모두 빠져도 상관이 없어야 한다.
내친김에 더 작게 [0, ), [, ), … 으로 생각해 보면 [0, 10]까지의 숫자 중 , , … , ,까지 빠져도 되고, 숫자만 조절하면 어마어마한 개수의 점들이 빠질 수 있다는 것까지 생각이 이르게 된다. 이쯤 되니 우리가 길이를 제대로 재고 있긴 하나 라는 생각마저 들기도 한다.
길이는 어떻게 측정하는 것인가?

우리가 현재 사용하고 있는 길이, 무게, 크기 등에서 모두 위와 같은 현상이 나타난다. 그렇다면 우리가 무엇인가를 잘못하고 있는 것일까? 아님 무엇인가를 빼놓고 생각하는 것일까? 수학에서는 이런 것들을 엄밀하게 하기 위해서 ‘측도(measure)’라는 것을 정의하여 사용하고 있다. ‘측도’라는 것이 무엇인지 핵심적인 것만을 말하면 다음과 같다.
(1) 측도 함수 μ는 항상 0보다 크거나 같다.
(2) 아무것도 없는 집합의 측도 함숫값은 0이다.
(3) 어떤 집합 A를 측도 함수 μ로 측정한 값은 A를 서로 겹치지 않게 나눈 뒤, 각각을 잰 측정값을 더한 것과 같다.
이를 받아들이기 쉽게 길이에 빗대어 다시 말해보면 다음과 같다.
(1) 길이는 항상 0보다 크거나 같다.
(2) 아무것도 없는 것의 길이는 0이다.
(3) 어떤 물체 A의 길이는 그 물체를 겹치는 부분이 없게 길이를 나누어 잰 뒤 합한 것과 길이가 같다.

우리가 일반적으로 사용하는 ‘길이’와 같은 측도 함수는 르베그 측도 함수로, 이는 측도 이론에 큰 공헌을 한 앙리 르베그(Henri Lebesgue)에서 따온 것이다. 이제, 이를 가지고 [0, 10]의 길이를 측정해 보자.
그럼 대체 [0, 10]과 (0, 10)의 길이는 몇이라고 해야 할까?
결론부터 말을 하자면 당연히 10이다. 물론 ‘어떤’ 측도 함수를 사용했는지에 따라 다르지만 르베그 측도 함수로는 10이 나온다. 다음은 우리가 길이를 재기 위해 사용할 르베그 측도 함수의 정의이다.
어려운 공식처럼 보이는 이것을 말로 풀어서 쓰면 ‘A를 모두 덮을 수 있도록 (겹치든 겹치지 않든) 열린 구간들을 모은 것들의 길이를 합한 것 중 최대 하계(하한)’가 된다. 하계란 어떤 수가 가질 수 있는 범위보다 작은 수로서, 만약 ‘x 〉 3’이라면 0과 3 모두 x가 될 수 있는 어떤 수보다도 작은 수이기에 하계이다. 하지만 3보다 큰 수들은 x가 될 수 있기에 3을 x의 최대 하계 또는 하한이라 부른다. 이제, 우리는 [0, 10]과 (0, 10)의 길이를 잴 준비가 되었다. 열린 구간 (0, 10)의 길이는 처음부터 열린 구간 그 자체이므로 하한 값은 자기 자신인 10이다. (열린 구간 (a, b)의 길이는 b-a로 정의한다.) 여기에 또한, [0, 10]의 닫힌 구간은 (-,)와 (0, 10), (,)로 덮을 수 있는데 이때의 각각의 길이 합은 1+10+1=12이지만 0과 10을 덮기 위해 추가한 (-,)와 (,)를 (-,)와 (,)로 바꿔도 모두 덮을 수 있으므로 0.2+10+0.2=10.4로 길이가 줄게 된다. 같은 방식으로 계속 길이를 줄여나갈 수 있지만 아무리 줄어들어도 10 이하로는 내려가지 않는다는 것을 알 수 있는데, 이렇게 더 이상 내려갈 수 없는 값들 중 가장 큰 값(여기서는 10)을 하한이라고 한다.
그런데 아직 의문은 풀리지 않았다. (0, 10)과 [0, 10]의 길이가 같다는 것은 알게 되었지만 그럼 ‘점을 몇 개나 빼도 길이가 같은 걸까?’라는 의문은 아직 풀리지 않은 것이다. 이에 대해서 이야기하려면 다분한 수학용어들이 등장하기에 간략히 하자면 ‘셀 수 있을 만큼 많이’ 점을 빼도 길이는 똑같다.
수학에서는 무한히 많은 것들에 대해서도 ‘셀 수 있을 만큼 많은’과 ‘셀 수 없을 만큼 많은’으로 경우를 나누는데, 분수 형태로 표시할 수 있는 유리수는 셀 수 있을 만큼 많은 경우며, 무리수의 개수는 셀 수 없을 만큼 많은 경우다. 따라서 [0, 10] 사이에 존재하는 모든 유리수를 모아서 르베그 측도로 길이를 재면 그 값은 0이 나오고, 무리수만 모아서 재도 0이 나온다. 이는 이해를 돕기 위해 예를 든 것으로, 셀 수 없이 많은 점을 모아 르베그 측도 값을 재도 0이 나오는 경우가 있음을 알아야 한다.
대체 무엇을 측정할 수 있을까?

수학이라는 것은 일반인이 보기에 살아가는 데 별 필요 없는 학문일지도 모른다. 지금까지 이야기한 측도에 관한 것도 쓰임새가 없다면 그렇게 보일지 모른다. 하지만 이러한 측도 이론은 현대를 살아가는 우리에게 너무나도 익숙한 확률과 큰 연관성이 있다. 러시아 수학자인 안드레이 니콜라에비치 콜모고로프(Andrey Nikolaevich Kolmogorov)는 독립적으로 연구되어 오던 측도 이론과 확률론을 결합하여 현대 확률론의 바탕을 마련했다. 확률에는 주사위의 1, 2, 3, 4, 5, 6처럼 값이 딱딱 떨어지는 표본이 있는 반면, 한 공장에서 만들어진 전구의 수명처럼 값이 떨어지는 것이 아닌 연속적으로 이어질 수 있는 경우가 있다. 예를 들어 전구의 수명이 5년 이상이라고 하는 것은 만들어지는 모든 전구의 수명이 5년 이상이라는 것이 아니라 수명이 5년 미만인 전구가 나올 확률이 0이라는 것이다. 콜모고로프 이전의 확률론은 주사위의 경우와 전구의 수명 같은 경우를 따로 계산했지만, 콜모고로프 이후의 확률론은 각 확률을 계산하는 변수의 ‘측도’를 달리하여 계산한다. 주사위의 경우 모든 경우를 ‘각각 세는 측도’이지만 전구 수명의 경우 ‘측도 함숫값이 0인 변수 부분은 제외’하고 계산하는 것이다. 콜모고로프 이후 많은 발전을 이룬 확률론은 경제, 통계학에 사용됨은 물론 현대물리의 정수라 불리는 양자역학 또한 ‘확률론적 결정론’이 적용된다.
‘확률이 0’≠‘불가능’?
소위 ‘확률이 0이다’라는 것을 ‘불가능하다’라는 것과 똑같다고 생각하지만 확률론에서는 두 가지를 서로 다르다고 정의한다. 다트 게임을 생각해 보자.
구역마다 정해진 점수가 있지만 구역을 나누는 경계선은 항상 논쟁거리인데, 일반적으로 경계선에 맞았을 경우 두 구역 중 높은 점수를 얻는 것으로 되어 있다. 만약 다트의 끝이 선과 같이 매우 가늘다면 다트가 경계선에 맞을 확률은 몇이나 될까? 르베그 측도에서 다시금 생각해 보면 다트 게임판에서 얇은 선이 차지하는 면적은 0이 되는데, 이를 바꾸어 말하면 다트로 선을 정확히 맞힐 확률은 0을 뜻하게 된다. 하지만 우리는 다트 게임 혹은 양궁에서 보듯이 불가능하지는 않다는 것을 몸으로 체감하고 있다.
손에서 떠나 표적 바로 앞까지 진행한 다트가 순간 사라진다거나 이미 맞은 위치가 바뀐다거나 하는 일은 ‘불가능’한 일이다.
어쩌면 이것이 의미하는 바가 리우올림픽에서 펜싱의 박상영 선수가 10-14로 몰린 상황에서 역전해 금메달을 차지한 것처럼 눈앞에 분명히 있지만 성공 확률이 매우 낮은 것도 노력하면 이룰 수 있다는 희망적인 메시지가 아닌가 하고 생각해 본다.⊙
월간조선
댓글 없음:
댓글 쓰기