Below are several figures for various points related to triangles. These include the centroid, the circumcenter, the orthocenter, the incenter, the excenters, and the Euler line (which is a line, rather than a point-- can you trust anything I say?).
This
page requires a java-enabled browser for correct functioning. The bright red
points (A, B, and C) can be moved around with the mouse and the figure will
adjust accordingly.
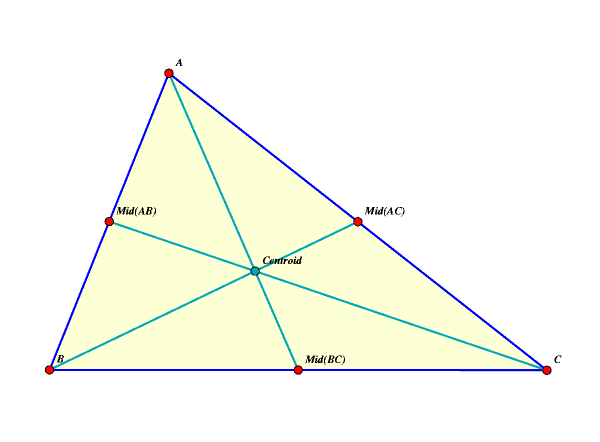
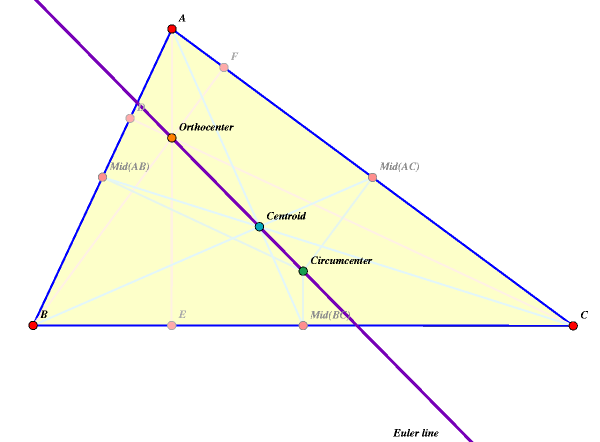
The centroid of a triangle is the point at
which the three medians meet. A median is the line between a vertex and the
midpoint of the opposite side.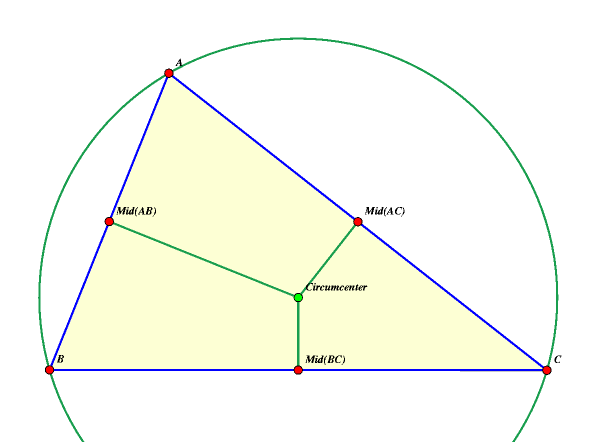 The three perpendicular bisectors of the sides of a triangle meet at the circumcenter. The circumcenter is also the center of the circle passing through the three vertices, which circumscribes the triangle. This circle is sometimes called the circumcircle. 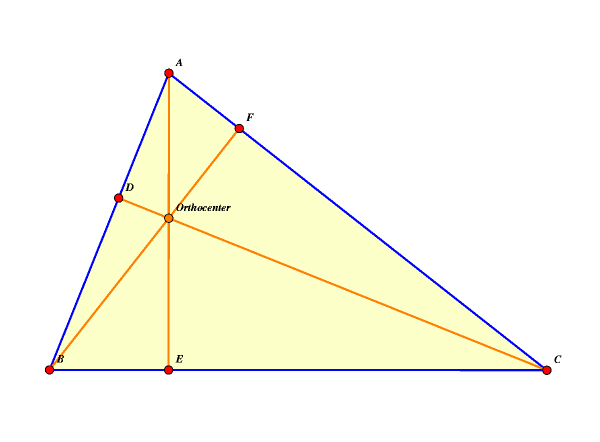 The orthocenter is the point of intersection of the altitudes of the triangle, that is, the perpendicular lines between each vertex and the opposite side.
When
the orthocenter is combined with the three vertices, any one of the points is
the orthocenter of the other three. This same property holds for the set of four
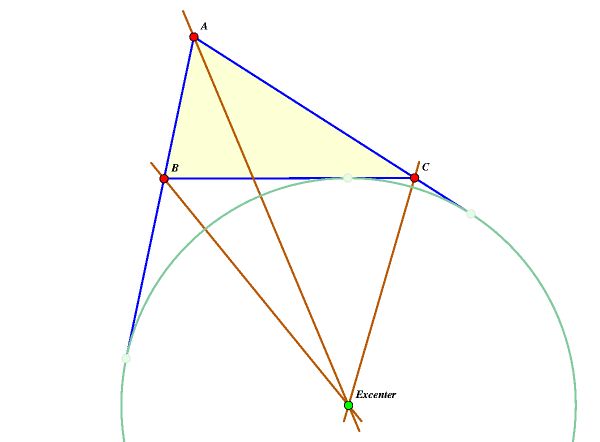
points consisting of the incenter and the three excenters. Such points are said to form an orthocentric system. Any three points from an orthocentric
system all have the same nine-point circleassociated with them.
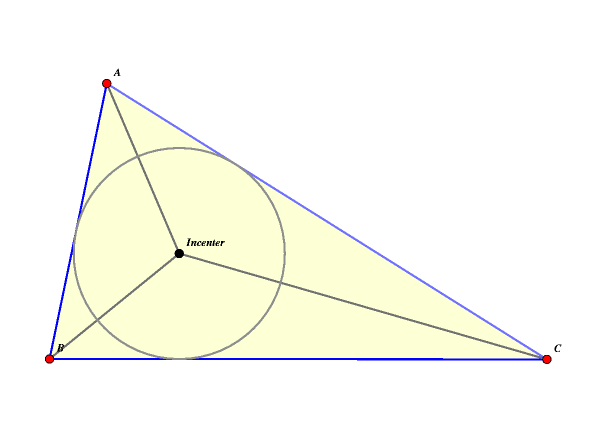
The incenter of
the triangle is the point at which the three bisectors of the interior angles of
the triangle meet. This is also the center of the inscribed
circle,
also called the incircle of
the triangle.
  |
|
The Euler line of a triangle is the line
that passes through the orthocenter, the circumcenter, and the centroid. It also contains the center of the Nine Point Circle. |
댓글 없음:
댓글 쓰기