Every rhombus is a parallelogram, and a rhombus with right angles is a square. (Euclid's original definition and some English dictionaries' definition of rhombus excludes squares, but modern mathematicians prefer the inclusive definition.)[1]
Etymology
The word "rhombus" comes from the Greek ῥόμβος (rhombos), meaning something that spins,[2] which derives from the verb ρέμβω (rhembō), meaning "to turn round and round".[3] The word was used both by Euclid and Archimedes, who used the term "solid rhombus" for two right circular cones sharing a common base.[4]
Characterizations
A simple (non self-intersecting) quadrilateral is a rhombus if and only if it is any one of the following:[5][6]- a quadrilateral with four sides of equal length (by definition)
- a quadrilateral in which the diagonals are perpendicular and bisect each other
- a quadrilateral in which each diagonal bisects two opposite interior angles
- a parallelogram in which at least two consecutive sides are equal in length
- a parallelogram in which the diagonals are perpendicular
- a parallelogram in which a diagonal bisects an interior angle
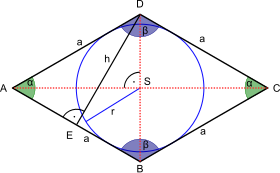
Basic properties
Every rhombus has two diagonals connecting pairs of opposite vertices, and two pairs of parallel sides. Using congruent triangles, one can prove that the rhombus is symmetric across each of these diagonals. It follows that any rhombus has the following properties:- Opposite angles of a rhombus have equal measure.
- The two diagonals of a rhombus are perpendicular; that is, a rhombus is an orthodiagonal quadrilateral.
- Its diagonals bisect opposite angles.
A rhombus is a tangential quadrilateral.[7] That is, it has an inscribed circle that is tangent to all four of its sides.
Area
As for all parallelograms, the area K of a rhombus is the product of its base and its height. The base is simply any side length a, and the height h is the perpendicular distance between any two non-adjacent sides:Inradius
The inradius (the radius of the incircle) can be expressed in terms of the diagonals p and q as[7]Dual properties
The dual polygon of a rhombus is a rectangle:[8]- A rhombus has all sides equal, while a rectangle has all angles equal.
- A rhombus has alternate angles equal, while a rectangle has alternate sides equal.
- A rhombus has an inscribed circle, while a rectangle has a circumcircle.
- A rhombus has an axis of symmetry through each pair of opposite vertex angles, while a rectangle has an axis of symmetry through each pair of opposite sides.
- The diagonals of a rhombus intersect at equal angles, while the diagonals of a rectangle are equal in length.
Other properties
- One of the five 2D lattice types is the rhombic lattice, also called centered rectangular lattice.
- Identical rhombi can tile the 2D plane in three different ways, including, for the 60° rhombus, the Rhombille tiling.
- Three-dimensional analogues of a rhombus include the bipyramid and the bicone.
References
- ^ Weisstein, Eric W., "Square" from MathWorld. inclusive usage
- ^ ῥόμβος, Henry George Liddell, Robert Scott, A Greek-English Lexicon, on Perseus
- ^ ρέμβω, Henry George Liddell, Robert Scott, A Greek-English Lexicon, on Perseus
- ^ The Origin of Rhombus
- ^ Zalman Usiskin and Jennifer Griffin, "The Classification of Quadrilaterals. A Study of Definition", Information Age Publishing, 2008, pp. 55-56.
- ^ Owen Byer, Felix Lazebnik and Deirdre Smeltzer, Methods for Euclidean Geometry, Mathematical Association of America, 2010, p. 53.
- ^ a b Weisstein, Eric W., "Rhombus" from MathWorld.
- ^ de Villiers, Michael, "Equiangular cyclic and equilateral circumscribed polygons", Mathematical Gazette 95, March 2011, 102-107.



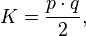

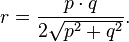
댓글 없음:
댓글 쓰기