세상을 바꾼 '몇 어찌' 기하학 (幾何)

성경 다음 많이 읽힌 '기하학 원론' 이집트 토지 측량에서 이름 탄생
그리스 거쳐 중세 유럽에서 재발견, 뉴턴의 운동법칙도 도형으로 기술돼
公理에 바탕 둔 증명은 철학에 영향… 美 독립선언서도 바탕은 수학 논리

 

 

인류 역사상 서구 문명에서 가장 많이 읽힌 책은 성경(聖經)이다. 그렇다면 그다음으로 많이 읽힌 책은 무엇일까. 네덜란드 수학자 루카스 번트는 "1482년 베니스에서 처음 인쇄본이 나온 '기하학 원론'은 이후 1000쇄 이상 발간돼 서구 문명에서 성경 다음으로 많이 보급된 책"이라고 밝혔다. 이 책은 기원전 3세기 그리스의 수학자 에우클레이데스가 썼다. 에우클레이데스는 우리에게 유클리드라는 영어 이름으로 알려진 인물이다.

수학이라고 하면 대부분 고개를 돌리지만 사실 우리나라는 세상 어디에도 없는 수학 교육의 전통이 있다. 수학을 국어책에서 가르친 유일한 나라이기 때문이다. 바로 유클리드의 기하학이다. 기하학은 중학교에 들어가면 배운다. 수학 선생님이 커다란 나무 각도계와 자를 들고 칠판 가득 선과 도형을 그리며 가르치는 것이 바로 기하학이다. 그런데 지금 중년들이 중학생 시절 배웠던 국어책에 나오는 고(故) 양주동(1903~1977·국문학자 겸 영문학자) 선생의 수필에 바로 그 기하학이 등장했다.

생전 '인간 국보 1호'라고 자칭했던 양주동 선생은 어린 시절 사서삼경 등 한문만 배웠다고 한다. 그가 신학문을 접한 것은 3·1운동 이듬해였다. 중학교의 전 과정을 단 1년에 수료하는 중학 속성과에 입학한 것이다. 선생은 개학 전날 새로 산 교과서를 훑어보았다. 그때 선생의 눈에 참 기괴한 단어가 들어왔다. 바로 '기하(幾何)'였다. '기(幾)'는 '몇'이란 뜻이요, '하(何)'는 '어찌'란 뜻이니 '기하'는 '몇 어찌'가 된다. 도대체 '몇 어찌'를 가르치는 수업은 무엇이란 말인가.

첫 기하 시간에 학생의 엉뚱한 질문을 받은 선생님은 이렇게 답했다. 영어의 '지오메트리(geometry)'를 중국 명나라 말기의 서광계가 중국어로 옮길 때 '지오'를 따서 '지허'라고 음역(音譯)한 것인데, 이를 우리 한자음을 따라 '기하'라고 하게 된 것이란 설명이었다.

기하학의 시초는 고대 이집트 문명이다. 이집트에서는 매년 나일강이 범람하고 나면 내 땅이 어디까지인지 구별이 되지 않았다. 이를 해결하기 위해 기하학이 발전했다. 기원전 5세기의 그리스 역사가 헤로도토스는 이집트 기행문에서 "이집트에서는 대홍수로 땅이 유실되면 측량 후 유실된 땅만큼 세금을 빼줬다. 여러 가지 꼴(도형)의 토지 넓이를 재는 기술이 발달했다"고 적었다. '기하학(geo+metry)'이란 말이 그리스어로 '토지(geo)'와 '측량(metry)'을 더해 만들어진 것도 이집트에서 근원을 찾을 수 있다.

일러스트=이철원 기자

이집트의 기하학은 그리스를 거쳐 유럽에서 부활했다. 중세 대학은 고대 그리스의 전통을 따라 산술·기하·천문·음악 등 수학과 관련된 네 과목을 자유교양 과목의 상급 4과목으로 삼았다. 나중에 뉴턴의 법칙을 낳은 것도 기하학이었다. 뉴턴이 세상 만물의 운동 법칙을 기술한 '프린키피아'는 수식이 아니라 순전히 도형으로 가득 찬 기하학 책이었다.

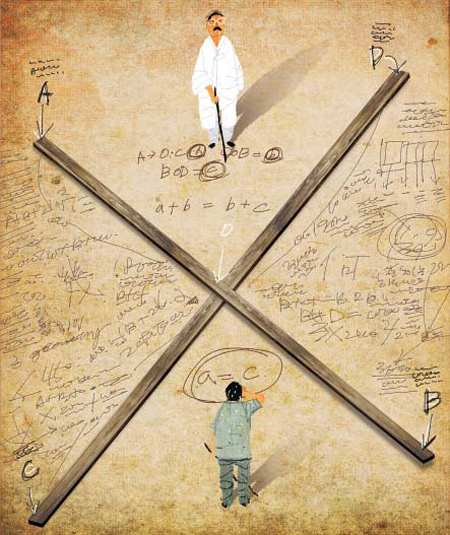
기하학의 영향은 비단 과학에 그치지 않았다. 철학에도 엄청난 영향을 미친 것이다. 우리는 이 역시 국어 시간에 배웠다. 양주동 선생의 수필에는 기하학의 정리를 배우는 장면이 나온다. 기하책에는 '정리(定理)란 증명을 요하는 진리'라고 나왔다. 다음 기하 시간에 선생님은 '맞꼭지각은 서로 같다'라는 정리를 증명하라고 했다. 어린 양주동은 반발했다. "두 곧은 막대기를 가위 모양으로 교차, 고정시켜 놓고 벌렸다 닫았다 하면 아래위의 각이 서로 같을 것은 정한 이치인데 무슨 다른 '증명'이 필요하겠습니까?"

선생님은 그건 비유지 증명이 아니라고 했다. 선생님의 증명은 이랬다. 두 선분을 교차하도록 긋는다. 한 선분의 끝은 A와 B, 다른 선분의 끝은 C와 D, 그리고 교차점을 O라 한다. A와 O·C가 만드는 각은 a, COB는 b, BOD는 c라 한다. 즉 a와 c는 서로 마주 보는 맞꼭지각이다. 선생님은 어린 양주동과 대화를 시작했다. "a+b는 몇 도?" "180도입니다." "b+c도 180도이지?" "예." "그럼, a+b=b+c이지?" "예." "그러니까, a=c 아니냐." 양 선생은 그 과학적·실증적 학풍 앞에서 아찔한 현기증을 느꼈다고 했다.

공리(公理)를 바탕으로 한 증명은 스피노자의 윤리학을 거쳐 미국 독립선언서로 이어졌다. 독립선언서는 "모든 사람은 평등하게 태어났다"로 시작해 "영국으로부터 독립해야 한다"는 결론을 이끌어냈다. 즉 아무도 부정하지 못하는 공리에서 시작해 논리적 추론으로 결론을 이끌어내는 '기하학 원론'의 방식을 그대로 쓴 것이다.

13일 서울에서 열린 세계수학자대회 개막식에서 마리암 미르자카니 미국 스탠퍼드대 교수가 여성으로는 처음으로 '수학의 노벨상' 필즈상을 받았다. 미르자카니 교수는 기하학 분야에서 탁월한 업적을 이룬 공을 인정받았다. 이집트에서 탄생한 '몇 어찌'가 수천 년을 이어 서울에서 빛을 발한 것이다

조선일보