20세기의 물리학의 두가지 위대한 업적을 꼽는다면 상대론과 양자론을 택할 것이다. 상대론은 아인슈타인이라는 천재에 의하여 단독으로 이루어졌지만 양자론은 보어(N.Bohr), 하이젠베르크(W.Heisenberg),슈뢰딩거(E.Schrödinger) 폴 디락(Paul Dirac) 4명의 거두들이 합작으로 이루어 낸 결과물이라 할 수 있다.
네 명의 거두들 가운데 디락의 방정식은 특수 상대론적 양자역학 방정식이다. 일반 상대론적 양자방정식은 아직은 알아내지 못하고 있는데 소위 말하는 ‘초끈이론’의 발달에 일말의 희망을 걸고 많은 물리학자와 수학자들이 연구를 하고 있다.
오늘 소개할 와일 전자를 세상에 선보인 헤르만 와일(Herman Weyl, 1885∼1955)은 널리 알려진 수리·물리학자이다. 그는 물리학계에 대칭성이란 개념을 확고하게 심어준 과학자이며 이 세상의 원리를 높은 곳에서 바라보는 독수리형 수리·물리학자이기도 하다.
명왕성을 예측했던 같은 해에 와일 전자도 예측
와일은 아인슈타인과도 친했으며 1918년에는 고전적인 게이지 이론을 전자기학에 도입한 선구자이기도 하다. 와일은 디락 방정식을 두 개의 질량 없는 전자의 방정식으로 고친 ‘와일 전자의 이론’을 도입했다. 85년 전인 1930년 명왕성을 예측했던 같은 해에 와일 전자도 예측되었다. 그런데 드디어 올해 6월 ‘사이언스’지에 프린스턴 대학교의 하산(M.zahid Hassan) 교수에 의해 와일 전자가 발견되었다는 소식이 실렸다.
와일 전자를 설명하려면 전자의 이론을 확고히 한 디락 방정식 이야기부터 시작해야 할 것 같다. 디락 방정식은 슈뢰딩거 방정식을 특수상대론에 맞도록 고친 방정식으로써 네 개의 연립방정식으로 되어 있다. 따라서 네 개의 해답이 있고, 그 중 두 개는 스핀 1/2 의 성분이 1/2 인 것과 –1/2인 것에 해당한다.
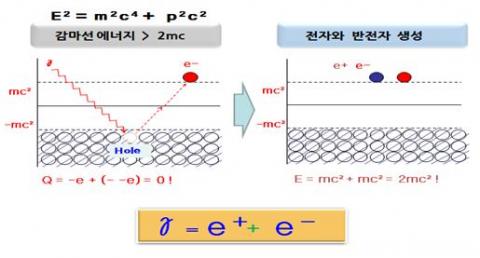
그런데 나머지 두 개는 전자의 에너지가 마이너스에 해당하는 해답으로 자연에 맞지 않는다. 그래서 디락은 이런 마이너스 에너지 상태는 가득 차 있으며, 전자의 질량 두 배에 해당하는 E = 2mc2 의 에너지를 진공에 공급하면 가득 차 있던 – 에너지 상태의 한 전자를 + 상태로 올려놓게 된다. 그렇게 되면 전기량이 0인 진공에서 – 전기량이 빠져나가게 되므로 이는 진공에 비하면 + 가 되고 이를 양전자(Positron)라고 해석했다.
디락 방정식은 이렇게 네 개의 복소수 방정식이다. 그런데 와일과 에토레 마조라나(Ettore Majorana: 1906~?)가 각각 두 개의 실수 방정식으로 고쳐 썼다. 마조라나의 방정식은 중성미자에 적용되리라 믿어지고 있다. (마조라나에 관한 이야기는 지난 7월 28일자와 8월 3일자의 ‘김제완의 과학세상’ 참고)
와일 전자는 질량이 없기 때문에 빛의 속도를 갖고 있다. 그 스핀의 방향이 와일 전자의 진행 방향과 평행한 것과 그 반대 방향인 두 종류로 되어 있다. 그런데 질량이 0인 입자는 특별한 주의가 필요하다. 가령, 와일 전자가 오는 방향 앞에 전기를 많이 띈 동판을 갖다 놓았다고 하자.
프린스턴대학팀 ”와일 전자가 반원 모양의 아치형을 그리며 전파”
와일 전자는 질량이 없기 때문에 이 판에 가까이와도 여전히 빛의 속도를 유지할 것 같다.그런데 이 동판에 부딪히는 순간 어떻게 될까? 없어질까? 또는 반대 방향으로 되돌아갈까? 그 해답은 물리를 전공하는 필자로서도 퍽 어렵고 아리송한 생각이 든다.
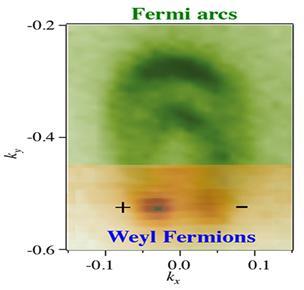
프린스턴대학팀이 제시한 실험 결과를 보면, 와일 전자가 반원 모양의 아치형을 그리며 전파하는 것을 제시하고 있다.
그들은 이런 현상을 반금속체인 Ta As(Tantalum Arsenide:탄탈륨 비소) 결정체를 써서 실험을 했다. 실험의 구체적인 내용은 필자도 잘 모르고 있다. 그러나 와일 전자를 생산하고, 이를 이용하면 소위 말하는 양자 컴퓨터에 큰 도움이 될 것이다. 첫 번째로는 전자가 빛의 속도로 전달되기 때문에 입출력(Input–Output) 과정이 획기적으로 빨라질 것이고, 계산 역시 빨라질 것이다.
연구자들의 말을 빌리면, 와일 전자는 질량이 없기 때문에 반대 방향으로 산란하는 것을 막아주어 효율을 획기적으로 높일 뿐만 아니라 열을 발생하지 않기 때문에 전력소모도 획기적으로 줄어들 것으로 전망하고 있다. 새로운 전산(컴퓨터)시대를 여는 열쇠가 85년 전에 예언되었다는 것은 퍽 인상적이다. 다시 한 번 수학의 위력에 고개를 숙이게 된다.
네 명의 거두들 가운데 디락의 방정식은 특수 상대론적 양자역학 방정식이다. 일반 상대론적 양자방정식은 아직은 알아내지 못하고 있는데 소위 말하는 ‘초끈이론’의 발달에 일말의 희망을 걸고 많은 물리학자와 수학자들이 연구를 하고 있다.
오늘 소개할 와일 전자를 세상에 선보인 헤르만 와일(Herman Weyl, 1885∼1955)은 널리 알려진 수리·물리학자이다. 그는 물리학계에 대칭성이란 개념을 확고하게 심어준 과학자이며 이 세상의 원리를 높은 곳에서 바라보는 독수리형 수리·물리학자이기도 하다.
명왕성을 예측했던 같은 해에 와일 전자도 예측
와일은 아인슈타인과도 친했으며 1918년에는 고전적인 게이지 이론을 전자기학에 도입한 선구자이기도 하다. 와일은 디락 방정식을 두 개의 질량 없는 전자의 방정식으로 고친 ‘와일 전자의 이론’을 도입했다. 85년 전인 1930년 명왕성을 예측했던 같은 해에 와일 전자도 예측되었다. 그런데 드디어 올해 6월 ‘사이언스’지에 프린스턴 대학교의 하산(M.zahid Hassan) 교수에 의해 와일 전자가 발견되었다는 소식이 실렸다.
와일 전자를 설명하려면 전자의 이론을 확고히 한 디락 방정식 이야기부터 시작해야 할 것 같다. 디락 방정식은 슈뢰딩거 방정식을 특수상대론에 맞도록 고친 방정식으로써 네 개의 연립방정식으로 되어 있다. 따라서 네 개의 해답이 있고, 그 중 두 개는 스핀 1/2 의 성분이 1/2 인 것과 –1/2인 것에 해당한다.
그런데 나머지 두 개는 전자의 에너지가 마이너스에 해당하는 해답으로 자연에 맞지 않는다. 그래서 디락은 이런 마이너스 에너지 상태는 가득 차 있으며, 전자의 질량 두 배에 해당하는 E = 2mc2 의 에너지를 진공에 공급하면 가득 차 있던 – 에너지 상태의 한 전자를 + 상태로 올려놓게 된다. 그렇게 되면 전기량이 0인 진공에서 – 전기량이 빠져나가게 되므로 이는 진공에 비하면 + 가 되고 이를 양전자(Positron)라고 해석했다.
디락 방정식의 해석. ⓒ 김제완
디락 방정식은 이렇게 네 개의 복소수 방정식이다. 그런데 와일과 에토레 마조라나(Ettore Majorana: 1906~?)가 각각 두 개의 실수 방정식으로 고쳐 썼다. 마조라나의 방정식은 중성미자에 적용되리라 믿어지고 있다. (마조라나에 관한 이야기는 지난 7월 28일자와 8월 3일자의 ‘김제완의 과학세상’ 참고)
와일 전자는 질량이 없기 때문에 빛의 속도를 갖고 있다. 그 스핀의 방향이 와일 전자의 진행 방향과 평행한 것과 그 반대 방향인 두 종류로 되어 있다. 그런데 질량이 0인 입자는 특별한 주의가 필요하다. 가령, 와일 전자가 오는 방향 앞에 전기를 많이 띈 동판을 갖다 놓았다고 하자.
프린스턴대학팀 ”와일 전자가 반원 모양의 아치형을 그리며 전파”
와일 전자는 질량이 없기 때문에 이 판에 가까이와도 여전히 빛의 속도를 유지할 것 같다.그런데 이 동판에 부딪히는 순간 어떻게 될까? 없어질까? 또는 반대 방향으로 되돌아갈까? 그 해답은 물리를 전공하는 필자로서도 퍽 어렵고 아리송한 생각이 든다.
프린스턴대학팀이 제시한 실험 결과를 보면, 와일 전자가 반원 모양의 아치형을 그리며 전파하는 것을 제시하고 있다.
와일 전자가 전파하는 모습. ⓒ 프린스턴대
연구자들의 말을 빌리면, 와일 전자는 질량이 없기 때문에 반대 방향으로 산란하는 것을 막아주어 효율을 획기적으로 높일 뿐만 아니라 열을 발생하지 않기 때문에 전력소모도 획기적으로 줄어들 것으로 전망하고 있다. 새로운 전산(컴퓨터)시대를 여는 열쇠가 85년 전에 예언되었다는 것은 퍽 인상적이다. 다시 한 번 수학의 위력에 고개를 숙이게 된다.
ScienceTimes
댓글 없음:
댓글 쓰기