2019년 2월 21일 목요일

수학의 재미 2019 AMC 10A Problem 6 문제해설

2019 AMC 10 문제: 다음 사각형의 4개 모든 꼭지점에서
같은 거리에있는 점이있는 도형은 몇개있는가?
정사각형
직사각형
마름모
평행사변형
등변사다리꼴

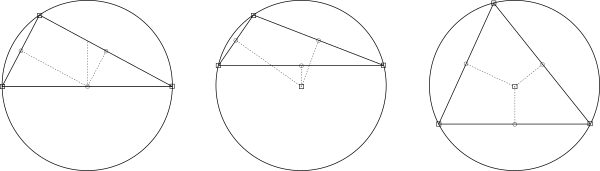
(1)각 사각형을 원안에 그리고 4 꼭지점이 모두 원주에 있다면 중심까지 거리가 같은 반지름이 존재하니까 거리가 같을수 밖에없다.

정사각형, 직사각형, 등변사다리꼴 3개가 답이다.
마름모 , 평행사변형은 그려보면 원주에 4점이 모두 없다.

cyclic quadrilaterals.

(2) 사각형을 그리고 각변의 수직이등분선을 그으면 한점에서 만난다

Circumscribed circle, C, and circumcenter, O, of a cyclic polygon, P

정사각형, 직사각형, 등변사다리꼴만 한점에서 만난다 .

마름모 , 평행사변형은 그려보면 한점에서 만나지 않는다

정사각형, 직사각형, 등변사다리꼴만 수직이등분선이 한점에서 만난다

삼각형의 외심

삼각형의 각 변의 수직이등분선의 교점은 외접원의 중심에서 만난다.

모든 삼각형에는 외심이 항상 존재하고, 그 점은 각 변의 수직이등분선의 교점이다. 그리고 삼각형의 각 꼭짓점에서 외심까지의 길이는 외접원의 반지름과 일치하므로 같다.

외심은 세 변의 수직이등분선의 교점이다.

2019 AMC 10 Problem

For how many of the following types of quadrilaterals does there exist a point in the plane of the quadrilateral that is equidistant from all four vertices of the quadrilateral?

a square
a rectangle that is not a square
a rhombus that is not a square
a parallelogram that is not a rectangle or a rhombus
an isosceles trapezoid that is not a parallelogram

$\textbf{(A) } 1 \qquad\textbf{(B) } 2 \qquad\textbf{(C) } 3 \qquad\textbf{(D) } 4 \qquad\textbf{(E) } 5$

Solution 1

This question is simply asking how many of the listed quadrilaterals are cyclic (since the point equidistant from all four vertices would be the center of the circumscribed circle). A square, a rectangle, and an isosceles trapezoid (that isn't a parallelogram) are all cyclic, and the other two are not. Thus, the answer is $\boxed{\textbf{(C) } 3}$ .

Solution 2

The perpendicular bisector of a line segment is the locus of all points that are equidistant from the endpoints. The question then boils down to finding the shapes where the perpendicular bisectors of the sides all intersect at a point. This is true for a square, rectangle, and isosceles trapezoid, so the answer is $\boxed{\textbf{(C) } 3}$ .

유사한 문제한번 풀어볼까요?
각변의 수직이등분선은 한점에서 만난다는 사실을 기억하고 풀어보세요
재미있을 겁니다
아무리해도 안풀리면 전화 하세요.
010-3549-5206

2015 AMC 10 문제

삼각형 $\triangle{ABC}$ 에서 $\angle{C} = 90^{\circ}$ $AB = 12$ 이다.

삼각형 $\triangle{ABC}$ 의 AC와 AB를 한변으로하는 정사각형 $ABXY$ 와 $ACWZ$ 을그리면
$X, Y, Z$ 와 W는 한원위에 놓이게된다.
삼각형 $\triangle{ABC}$ 의 둘레의 길이는 얼마인가?

2015 AMC 10B Problem 19

Problem

In $\triangle{ABC}$ , $\angle{C} = 90^{\circ}$ and $AB = 12$ . Squares $ABXY$ and $ACWZ$ are constructed outside of the triangle. The points $X, Y, Z$ , and $W$ lie on a circle. What is the perimeter of the triangle?

$\textbf{(A) }12+9\sqrt{3}\qquad\textbf{(B) }18+6\sqrt{3}\qquad\textbf{(C) }12+12\sqrt{2}\qquad\textbf{(D) }30\qquad\textbf{(E) }32$

Solution

The center of the circle lies on the perpendicular bisectors of both chords $ZW$ and $YX$ . Therefore we know the center of the circle must also be the midpoint of the hypotenuse. Let this point be $O$ . Draw perpendiculars to $ZW$ and $YX$ from $O$ , and connect $OZ$ and $OY$ . $OY^2=6^2+12^2=180$ . Let $AC=a$ and $BC=b$ . Then $\left(\dfrac{a}{2}\right)^2+\left(a+\dfrac{b}{2}\right)^2=OZ^2=OY^2=180$ . Simplifying this gives $\dfrac{a^2}{4}+\dfrac{b^2}{4}+a^2+ab=180$ . But by Pythagorean Theorem on $\triangle ABC$ , we know $a^2+b^2=144$ , because $AB=12$ . Thus $\dfrac{a^2}{4}+\dfrac{b^2}{4}=\dfrac{144}{4}=36$ . So our equation simplifies further to $a^2+ab=144$ . However $a^2+b^2=144$ , so $a^2+ab=a^2+b^2$ , which means $ab=b^2$ , or $a=b$ . Aha! This means $\triangle ABC$ is just an isosceles right triangle, so $AC=BC=\dfrac{12}{\sqrt{2}}=6\sqrt{2}$ , and thus the perimeter is $\boxed{\textbf{(C)}\ 12+12\sqrt{2}}$ . $[asy] /* Geogebra to Asymptote conversion, documentation at artofproblemsolving.com/Wiki, go to User:Azjps/geogebra */ import graph; size(11.5cm); real labelscalefactor = 0.5; /* changes label-to-point distance */ pen dps = linewidth(0.7) + fontsize(10); defaultpen(dps); /* default pen style */ pen dotstyle = black; /* point style */ real xmin = -4.3, xmax = 18.7, ymin = -5.26, ymax = 6.3; /* image dimensions */ draw((3.46,0.96)--(3.44,-3.36)--(8.02,-3.44)--cycle); draw((3.46,0.96)--(8.02,-3.44)--(12.42,1.12)--(7.86,5.52)--cycle); /* draw figures */ draw((3.46,0.96)--(3.44,-3.36)); draw((3.44,-3.36)--(8.02,-3.44)); draw((8.02,-3.44)--(3.46,0.96)); draw((3.46,0.96)--(-0.86,0.98)); draw((-0.86,0.98)--(-0.88,-3.34)); draw((-0.88,-3.34)--(3.44,-3.36)); draw((3.46,0.96)--(8.02,-3.44)); draw((8.02,-3.44)--(12.42,1.12)); draw((12.42,1.12)--(7.86,5.52)); draw((7.86,5.52)--(3.46,0.96)); draw((5.74,-1.24)--(-0.86,0.98)); draw((5.74,-1.24)--(-0.87,-1.18), linetype("4 4")); draw((5.74,-1.24)--(7.86,5.52)); draw((5.74,-1.24)--(10.14,3.32), linetype("4 4")); draw(shift((5.82,-1.21))*xscale(6.99920709795045)*yscale(6.99920709795045)*arc((0,0),1,19.44457562540183,197.63600413408128), linetype("2 2")); /* dots and labels */ dot((3.46,0.96),dotstyle); label("$A$", (3.2,1.06), NE * labelscalefactor); dot((3.44,-3.36),dotstyle); label("$C$", (3.14,-3.86), NE * labelscalefactor); dot((8.02,-3.44),dotstyle); label("$B$", (8.06,-3.8), NE * labelscalefactor); dot((-0.86,0.98),dotstyle); label("$Z$", (-1.34,1.12), NE * labelscalefactor); dot((-0.88,-3.34),dotstyle); label("$W$", (-1.48,-3.54), NE * labelscalefactor); dot((12.42,1.12),dotstyle); label("$X$", (12.5,1.24), NE * labelscalefactor); dot((7.86,5.52),dotstyle); label("$Y$", (7.94,5.64), NE * labelscalefactor); dot((5.74,-1.24),dotstyle); label("$O$", (5.52,-1.82), NE * labelscalefactor); clip((xmin,ymin)--(xmin,ymax)--(xmax,ymax)--(xmax,ymin)--cycle); [/asy]$

AoPS

댓글 없음:

댓글 쓰기