아폴로니오스의 정리(Apollonius' theorem)중선정리(中線定理) KMO 기하학 기초

작성된 태그가 없습니다.

태그달기

취소 확인

아폴로니오스의 정리(Apollonius' theorem) 또는 중선정리(中線定理)는 초등 기하학에서 삼각형의 각 변들간의 관계를 설명한 정리이다. '아폴로니오스'라는 이름은 고대 그리스의 수학자인 페르게의 아폴로니오스의 이름을 딴 것이다. 대한민국과 일본에서는 흔히 파푸스의 정리(Pappus's theorem)라는 이름으로도 알려져 있으나, 이외의 국가에서는 이러한 이름으로 불리지 않는다.

내용

Wikipedia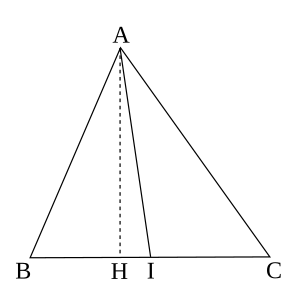

그림에서 <math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle BI=IC}"><semantics><annotation encoding="application/x-tex">{\displaystyle BI=IC}</annotation></semantics></math>일 때, 선분 <math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle AI}"><semantics><annotation encoding="application/x-tex">{\displaystyle AI}</annotation></semantics></math>는 중선(Median)이 되고, 다음의 관계가 성립한다.

<math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle AB^{2}+AC^{2}=2(BI^{2}+AI^{2})\,}"><semantics><annotation encoding="application/x-tex">{\displaystyle AB^{2}+AC^{2}=2(BI^{2}+AI^{2})\,}</annotation></semantics></math>

특히, <math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle AB=AC}"><semantics><annotation encoding="application/x-tex">{\displaystyle AB=AC}</annotation></semantics></math>가 성립할 경우, 피타고라스의 정리가 된다. 즉,

<math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle AI^{2}+BI^{2}=AB^{2}(=AC^{2})\,}"><semantics><annotation encoding="application/x-tex">{\displaystyle AI^{2}+BI^{2}=AB^{2}(=AC^{2})\,}</annotation></semantics></math>

이 정리는 스튜어트 정리에서 <math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle BI=IC}"><semantics><annotation encoding="application/x-tex">{\displaystyle BI=IC}</annotation></semantics></math>를 가정할 때와 동일하므로 스튜어트 정리의 특수한 형태가 된다.